Оглавление:
Сходящиеся последовательности
Определение 2.8. Число 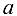 называется пределом числовой последовательности
называется пределом числовой последовательности 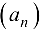 , если для
, если для 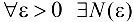 такой, что
такой, что 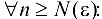
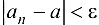 , т. е.
, т. е.
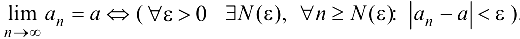
Последовательность, имеющая предел, называется сходящейся, в противном случае — расходящейся.
Из (2.1) рассмотрим условие 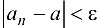 .
.
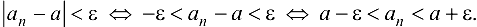
Последние неравенства означают, что при 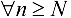 элемент последовательности
элемент последовательности 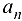 должен находиться в интервале
должен находиться в интервале 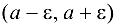 . Напомним, что данный интервал называется
. Напомним, что данный интервал называется 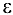 -окрестностыо точки
-окрестностыо точки 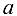 .
.
Определение 2.8′. Число а называется пределом числовой последовательности 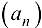 , если для
, если для 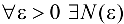 , начиная с которого все члены последовательности принадлежат
, начиная с которого все члены последовательности принадлежат 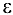 -окрестности точки
-окрестности точки 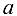 .
.
Геометрический смысл предела последовательности: 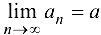 , если вне любой в-окрестности точки а имеется лишь конечное число членов этой последовательности.
, если вне любой в-окрестности точки а имеется лишь конечное число членов этой последовательности.
Пример 2.5.
Доказать, что 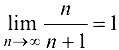 .
.
Решение:
Согласно условию, требуется доказать, что число «1» является пределом последовательности 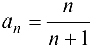 , т. е. для
, т. е. для 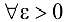 нужно указать номер
нужно указать номер 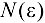 , начиная с которого для всех членов последовательности будет выполнено
, начиная с которого для всех членов последовательности будет выполнено 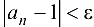 , т. е.
, т. е.
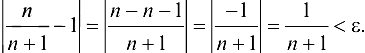
Из неравенства 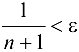 получаем
получаем 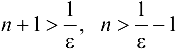 . Таким образом, для
. Таким образом, для 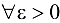 , полагая
, полагая 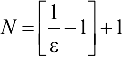 , получаем, что для
, получаем, что для 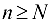 будет выполнено
будет выполнено 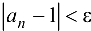 . Заметим, что величина
. Заметим, что величина 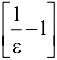 представляет собой целую часть выражения
представляет собой целую часть выражения 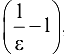 , тогда
, тогда 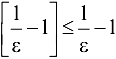 .
.
Поэтому для выполнения условия 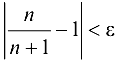 при
при 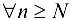 полагаем
полагаем 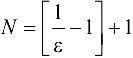 . ■
. ■
Теорема 2.2. Числовая последовательность 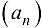 имеет своим пределом число «а» тогда только тогда, когда
имеет своим пределом число «а» тогда только тогда, когда
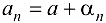
где 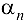 — члены БМП
— члены БМП 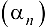 .
.
Доказательство.
Необходимость. Пусть 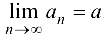 Обозначим
Обозначим 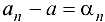 . Получим
. Получим 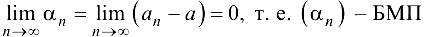 .
.
Достаточность. Пусть 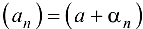 , где
, где 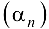 — БМП. Тогда
— БМП. Тогда 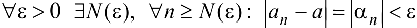 , т. е.
, т. е. 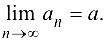 . ■
. ■
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

