Оглавление:
Схемы решения типовых задач
Говоря о специальных методах, приведём известные схемы раскрытия модулей, рассчитанные на определённые, наиболее часто встречающиеся виды уравнений и неравенств.
1) Уравнения вида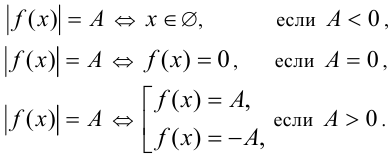 
Пример №293.
Решить уравнение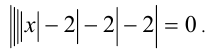 
Решение:
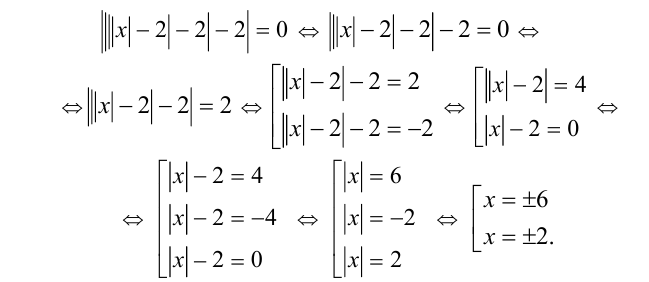
Пример №294.
При всех а решить уравнение
Решение:
а) При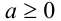 
имеем, в соответствие с данной схемой, что
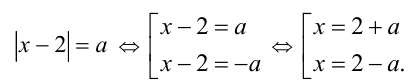
При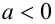 
решений нет
б) При всех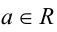 
имеем: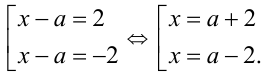 
Пример №295.
Сколько решений имеет уравнение
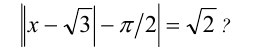
Решение:
Раскроем вначале внешний модуль, сведя уравнение к совокупности двух уравнений:
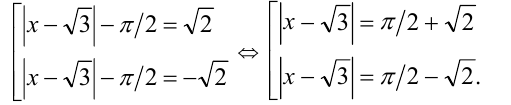
Правая часть первого уравнения положительна, поэтому оно имеет два различных решения (можно было бы даже найти эти решения:
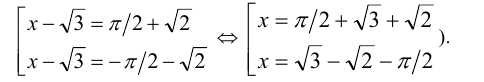
Чтобы узнать, имеет ли решения второе уравнение, оценим знак его правой части :
Известно, что 
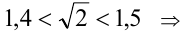
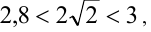а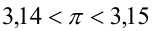 
. Из приведённых оценок следует, что 
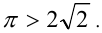Итак, второе уравнение также имеет два решения
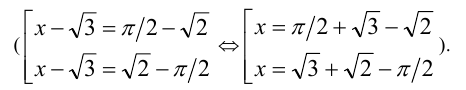
Так как все решения разные, то получаем ответ. Ответ: 4 решения.
Пример №296.
Решить уравнение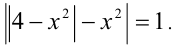 
Решение:
Эта задача также относится к указанному типу, но её можно решать иначе, начав с раскрытия внутреннего модуля:
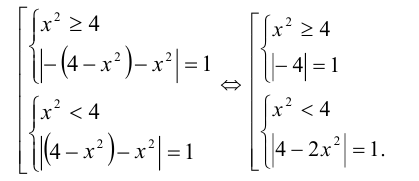
Первая из систем не имеет решений. Осталось решить вторую систему:
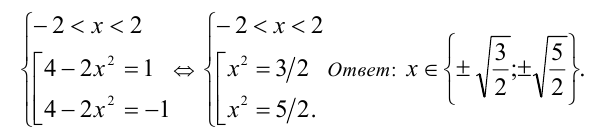
2) Неравенства вида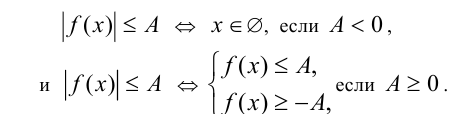 
Пример №297.
При всех а решить неравенство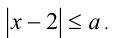 
Решение:
Действуя по предложенной схеме, сразу получаем ответ. Ответ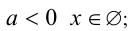: при 
при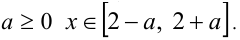 
Пример №298.
На плоскости Оху изобразить множество точек, координаты x и у которых удовлетворяют условию
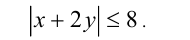
Решение:
Раскроем модуль: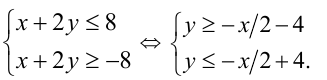 
Искомое ГМТ представляет собой полосу на координатной плоскости Оху,
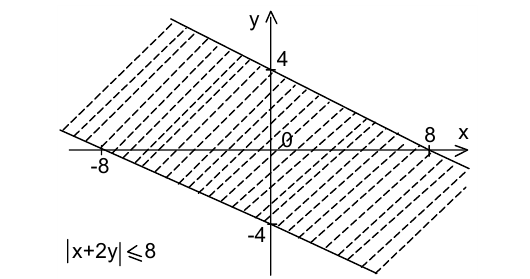
состоящую из точек, расположенных между двумя параллельными прямыми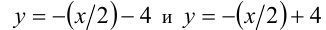 
(включая эти прямые)
3) Неравенства вида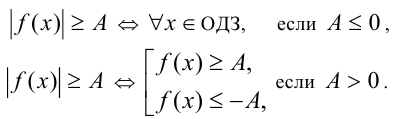 
Пример №299.
Решить неравенство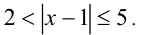 
Решение:
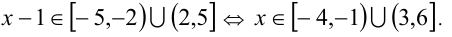
В других случаях бывает удобнее не применять этой схемы.
Пример №300.
Найти все целые значения x , для которых справедливо неравенство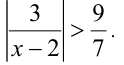 
Решение:
Воспользуемся приёмом обращения дроби:
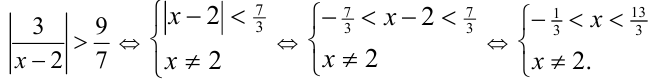
Осталось отобрать все целые x . Ответ: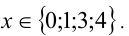 
4) Уравнения вида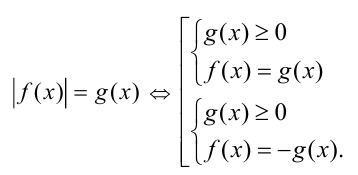 
Пример №301.
Решить уравнение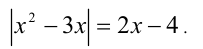 
Решение:
Воспользуемся указанным способом:
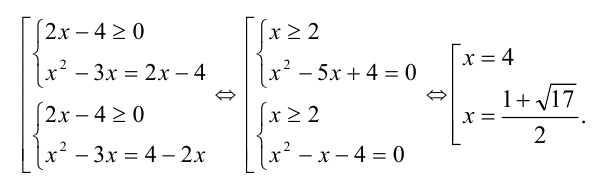
Пример №302.
Решить уравнение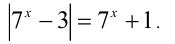 
Решение:
Так как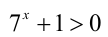 
при любом 
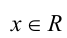, то уравнение равносильно совокупности
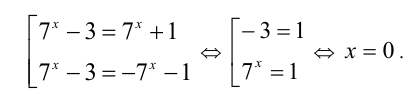
5) Неравенства вида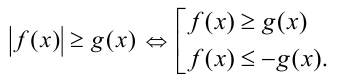 
Пример №303.
Решить неравенство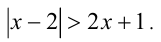 
Решение:
Данное неравенство равносильно совокупности неравенств
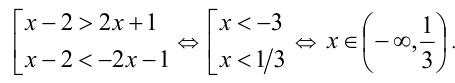
В других задачах бывает удобнее рассмотреть два случая:
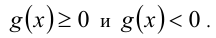
Пример №304.
Решить неравенство
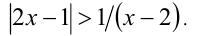
Решение:
При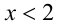 
левая часть неравенства неотрицательна, а правая — отрицательна, следовательно, все такие значения 
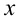будут решениями. Если же 
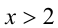, то имеем 
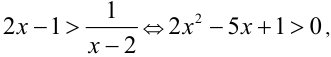откуда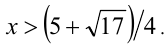 
Ответ: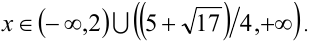
6) Неравенства вида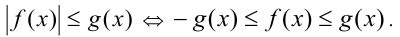 
Пример №305.
Решить неравенство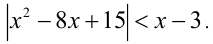 
Решение:
Сведём неравенство к равносильной ему системе
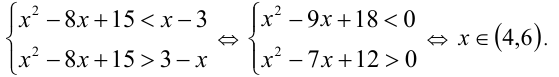
Пример №306.
Решить неравенство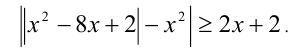 
Решение:
Имеем:
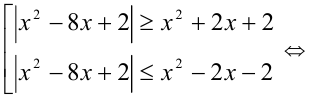
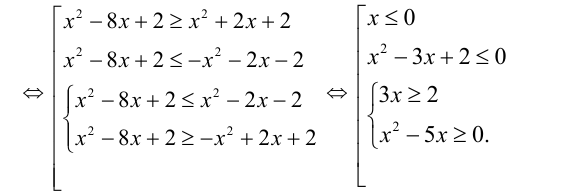
Ответ: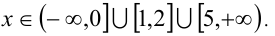 
Эта ссылка возможно вам будет полезна:
| Помощь по математике |
Пример №307.
При всех значениях параметра а решить неравенство
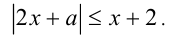
Решение:
Воспользуемся известным приёмом и получим, что неравенство равносильно системе неравенств
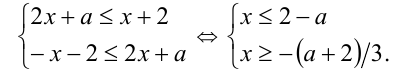
Очевидно, что данная система имеет решения тогда и только тогда, когда
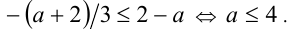
Эти решения x представляют собой отрезок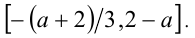 
Ответ: при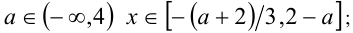 
при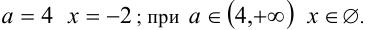 
7) Уравнения вида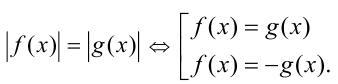 
Пример №308.
Решить уравнение
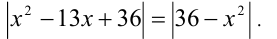
Решение:
Согласно предложенной схеме
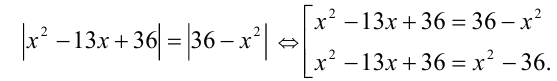
Решая совокупность уравнений, получаем ответ: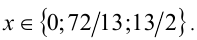 
Пример №309.
Решить уравнение
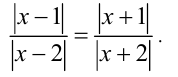
Решение:
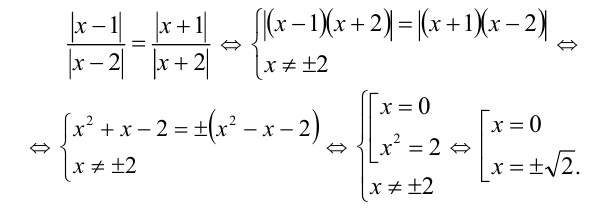
Пример №310.
Решить уравнение
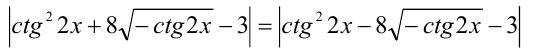
Решение:
Сделаем замену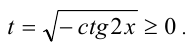 
Тогда уравнение примет алгебраическии вид
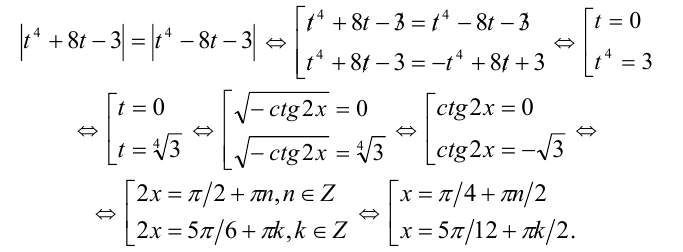
Ответ: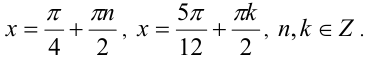 
8) Неравенства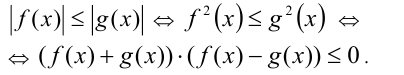 
Пример №311.
Найти наименьшее целое положительное число, удовлетворяющее неравенству
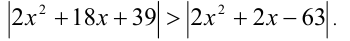
Решение:
Возведём данное неравенство в квадрат (равносильное преобразование)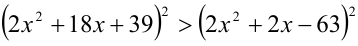 
и, не раскрывая квадратов, тут же перенесём все слагаемые в одну сторону и разложим на множители:
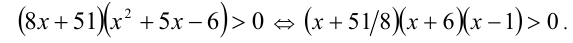
Решая это неравенство методом интервалов, получаем
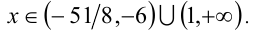
Ответ: наименьшее целое положительное число x есть 2.
Пример №312.
Решить неравенство
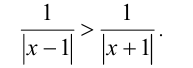
Решение:
Воспользуемся приёмом обращения дробей:
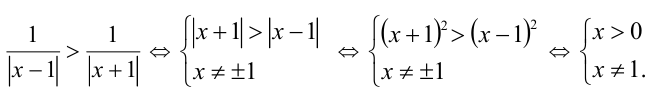
Ответ: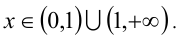 
9) Неравенства вида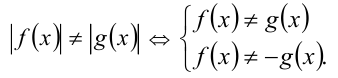 
Пример №313.
Решить неравенство
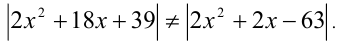
Решение:
Данное неравенство равносильно системе двух неравенств:
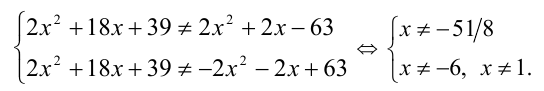
Ответ: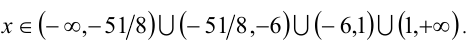 
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
