Схемы применения определенного интеграла
Пусть требуется найти значение какой-либо геометрической или физической величины  (площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т. д.), связанной с отрезком
(площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т. д.), связанной с отрезком  изменения независимой переменной
изменения независимой переменной  . Предполагается, что эта величина
. Предполагается, что эта величина  аддитивна, т. е. такая, что при разбиении отрезка
аддитивна, т. е. такая, что при разбиении отрезка  точкой
точкой 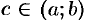 на части
на части 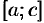 и
и 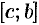 значение величины
значение величины  , соответствующее всему отрезку
, соответствующее всему отрезку  , равно сумме ее значений, соответствующих
, равно сумме ее значений, соответствующих 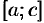 и
и 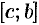 .
.
Для нахождения этой величины  можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала).
можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала).
Первая схема базируется на определении определенного интеграла.
1. Точками 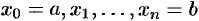 разбить отрезок
разбить отрезок  на
на  частей. В соответствии с этим, интересующая нас величина
частей. В соответствии с этим, интересующая нас величина  разобьется на
разобьется на  «элементарных слагаемых»
«элементарных слагаемых» 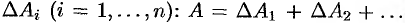
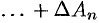 .
.
2. Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего отрезка на его длину: 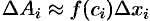 .
.
При нахождении приближенного значения 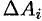 допустимы некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей ее концы; переменную скорость на малом участке можно приближенно считать постоянной и т. д.
допустимы некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей ее концы; переменную скорость на малом участке можно приближенно считать постоянной и т. д.
Получим приближенное значение величины  в виде интегральной суммы:
в виде интегральной суммы:
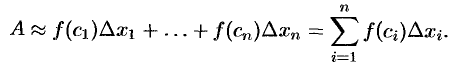
3. Искомая величина  равна пределу интегральной суммы, т. е.
равна пределу интегральной суммы, т. е.
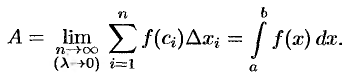
Указанный «метод сумм», как видим, основан на представлении интеграла как о сумме бесконечно большого числа бесконечно малых слагаемых.
Схема I была применена для выяснения геометрического и физического смысла определенного интеграла.
Вторая схема представляет собой несколько видоизмененную схему I и называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»:
1) на отрезке  выбираем произвольное значение
выбираем произвольное значение  и рассматриваем переменный отрезок
и рассматриваем переменный отрезок 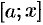 . На этом отрезке величина
. На этом отрезке величина  становится функцией
становится функцией  :
: 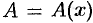 , т. е. считаем, что часть искомой величины
, т. е. считаем, что часть искомой величины  есть неизвестная функция
есть неизвестная функция 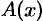 , где
, где 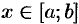 — один из параметров величины
— один из параметров величины  ;
;
2) находим главную часть приращения 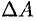 при изменении
при изменении  на малую величину
на малую величину 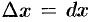 , т. е. находим дифференциал
, т. е. находим дифференциал 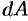 функции
функции 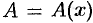 :
: 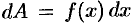 , где
, где  , определяемая из условия задачи, функция переменной
, определяемая из условия задачи, функция переменной  (здесь также возможны различные упрощения);
(здесь также возможны различные упрощения);
3) считая, что 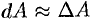 при
при 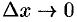 , находим искомую величину путем интегрирования
, находим искомую величину путем интегрирования 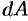 в пределах от
в пределах от 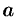 до
до 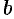 :
:
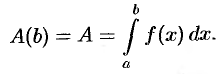
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Интеграл с бесконечным промежутком интегрирования |
| Интеграл от разрывной функции |
| Вычисление площадей плоских фигур |
| Вычисление длины дуги плоской кривой |

