Задача №1.1.6.
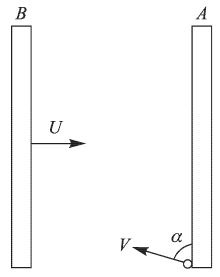
Шарик пренебрежимо малой массы начинает скольжение в горизонтальной плоскости от неподвижной доски 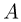 со скоростью
со скоростью 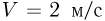 под углом
под углом 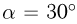 к ней. Доска
к ней. Доска 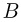 , параллельная доске
, параллельная доске 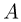 , движется перпендикулярно плоскости доски с некоторой скоростью
, движется перпендикулярно плоскости доски с некоторой скоростью 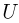 . Найти
. Найти 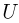 , если время движения шарика от доски
, если время движения шарика от доски 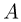 до встречи с доской
до встречи с доской 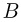 в
в 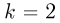 раза превышает время его движения обратно. Удар шарика о доску
раза превышает время его движения обратно. Удар шарика о доску 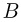 считать упругим. Трением пренебречь.
считать упругим. Трением пренебречь.
Решение:
Пусть расстояние между досками в начальный момент равно 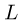 . По закону сложения скоростей величина нормальной к доске
. По закону сложения скоростей величина нормальной к доске 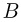 составляющей относительной скорости шарика до удара равна
составляющей относительной скорости шарика до удара равна 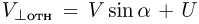 . Следовательно, время движения шарика до удара о доску
. Следовательно, время движения шарика до удара о доску 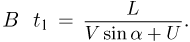 В системе отсчета, связанной с доской
В системе отсчета, связанной с доской 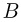 , скорость шарика после упругого удара остается той же самой по величине, а нормальная к доске составляющая скорости меняет направление на противоположное:
, скорость шарика после упругого удара остается той же самой по величине, а нормальная к доске составляющая скорости меняет направление на противоположное: 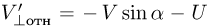 . Переходя в неподвижную систему отсчета по формуле
. Переходя в неподвижную систему отсчета по формуле 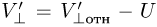 , находим, что после удара величина составляющей скорости шарика, нормальной к доске
, находим, что после удара величина составляющей скорости шарика, нормальной к доске 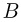 , станет равной
, станет равной 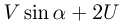 . Поэтому время обратного движения шарика до доски
. Поэтому время обратного движения шарика до доски 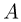 составит
составит 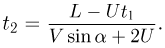
Учитывая, что 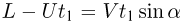 и используя условие
и используя условие 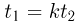 , получаем ответ:
, получаем ответ: 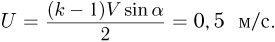
Эти задачи взяты со страницы решения задач по физической механике:
Решение задач по физической механике
Возможно эти задачи вам будут полезны:

