Оглавление:


Секториальные нормальные напряжения, векториальные характеристики сечения.
- Векторные характеристики разреза. §В § 173 и 174 были составлены уравнения равновесия для выбранной части стержня, учитывающие деформацию продольных волокон, возникшую в результате неравномерного разрушения соседних деталей. Теперь остается использовать комбинированное решение уравнения(30.1), (30.2), (30.3) и (30.10)определить величину золы. Подставляя значение (30.10)в
уравнение равновесия и суммируя область 6 «=остается постоянной с учетом, получаем:£6». J / 7=0 или JJzdF; (30.15)Swy=^y d F -, (30.16) Их размеры-это единица длины в пятой степени (например, см*). Чтобы связать фактор внешней силы и нормальное напряжение сектора, мы расширяем понятие изгибного крутильного бимомента как обобщенной силы; это соответствующее обобщенное-542 XXX. Сила этого движения! да что с тобой такое?
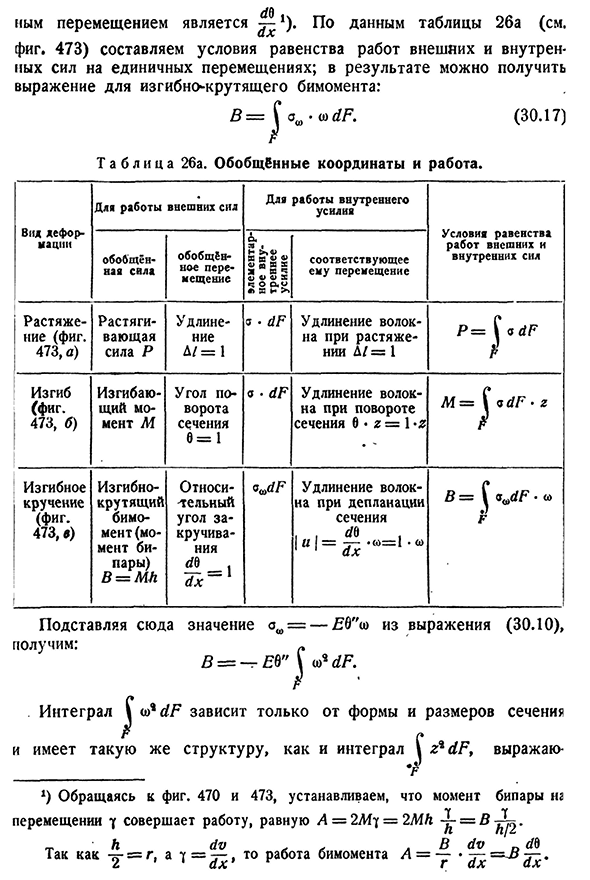
По данным таблицы 26а(см. рис. 473) составим условия равенства внешних и внутренних Людмила Фирмаль
сил работы на перемещение агрегата; в результате можно получить формулу для изгиба и кручения бимомента:=J• (30.17).) Т а б л и Ц а 26а. общие координаты и работа. Вид деформации Четыре. Для работы внешней силы для работы внутреннего усилия Условия равенства в работе внешних и обобщенных внутренних сил Обобщенное перемещение • CX I1 D D D F4) O d K S I D H Ф Ф Ф Ф Соответствующее движение Растяжка (рис. 473, а) Растягивающее усилие P Растяжка D / =1 Напряжение Д/=1,
удлиненность волокна а * ДФ П = ДФ Изгиб(рис. 473, б) Изгибающий момент м Секция 6=1 угол поворота Но. Удлинение нити dF на участке 6*z=1 * z вращение • М=<формат jdf * з Изгиб кручения Рисунок 4 7 3,.) Изгибающий момент бимомент (двудольный момент) B=Mh Относительный угол закручивания дБ Д х So > удлинение волокна dF при истощении поперечного сечения и= — *(0=1. (О » Д х Б=в^ДФ * совместное Ф Где значение ash= — Ed » Yu подставляется из Формулы (30.10)、: Интеграл J w4dF зависит только от формы и размеров
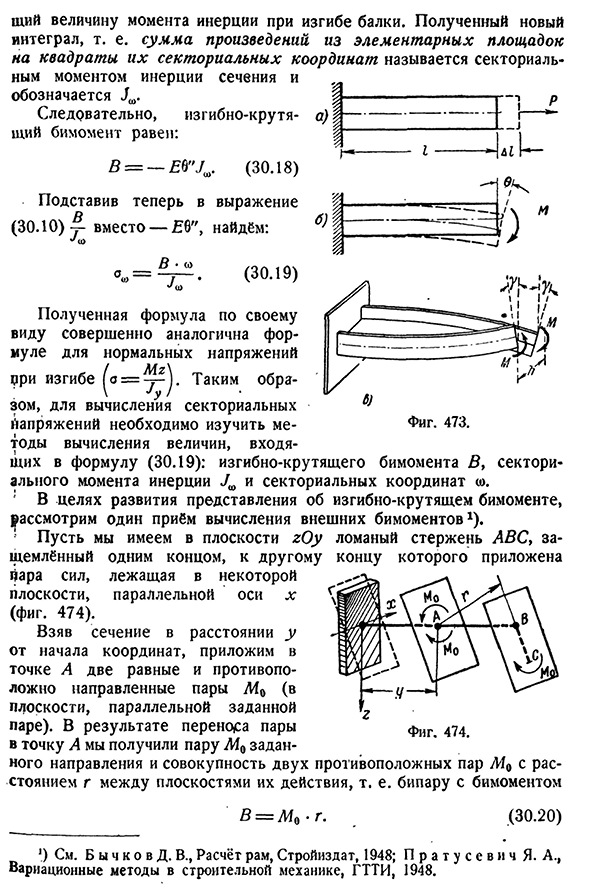
- сечения и имеет ту же структуру, что и Интеграл i z*dF, I Express-t Как использовать 470 и 473, мы устанавливаем момент гадюки на упражнении 7 в=2mu=22IL=делаем равную работу. Bymoment D=~t o RA^a t as a.§ 175] секторное нормальное напряжение 543 Величина момента инерции при изгибе балки. Полученный новый Интеграл, то есть сумма произведения от базового участка до x координат квадрата и сектора, называется моментом инерции сечения и показан на рисунке.: Б= — Е6 «Дж». (30.18) Теперь подставим в Формулу (30.10) — вместо-E6″, находим: *’<0 (30.19) Формула, полученная в ее виде, очень похожа на Формулу нормального изгибного напряжения=поэтому, чтобы рассчитать напряжение
сектора, необходимо изучить МЕ-рис 473 для вычисления значений, содержащихся в Формуле (30.19): крутящий момент-бимомент в, инерция-двигатель и координаты сектора со. Чтобы развить идею бимомента при изгибе и скручивании, рассмотрим 1 способ расчета внешних бимоментов1). ! Пусть сломанный стержень LAN зажат на одном конце в плоскости zoy, приложенный лежащим на некоторой параллельной оси X к другому концу. В Яра сил, самолет, (рис. 474). Взяв сечение на расстоянии y от начала координат, мы прикрепляем две равные и противоположно направленные пары к точке A (в плоскости, параллельной данной паре). В результате движения пары к точке А мы имеем пару L1o в заданном направлении и расстояние g между плоскостями их действия,
то есть двуногость с бимодальностью. В=В0-г(30.20) 9 см. б у Ч К О В Д. в., рамный калькулятор, стройздат, 1948;П Р А Т У С Е В и ч я. А., Людмила Фирмаль
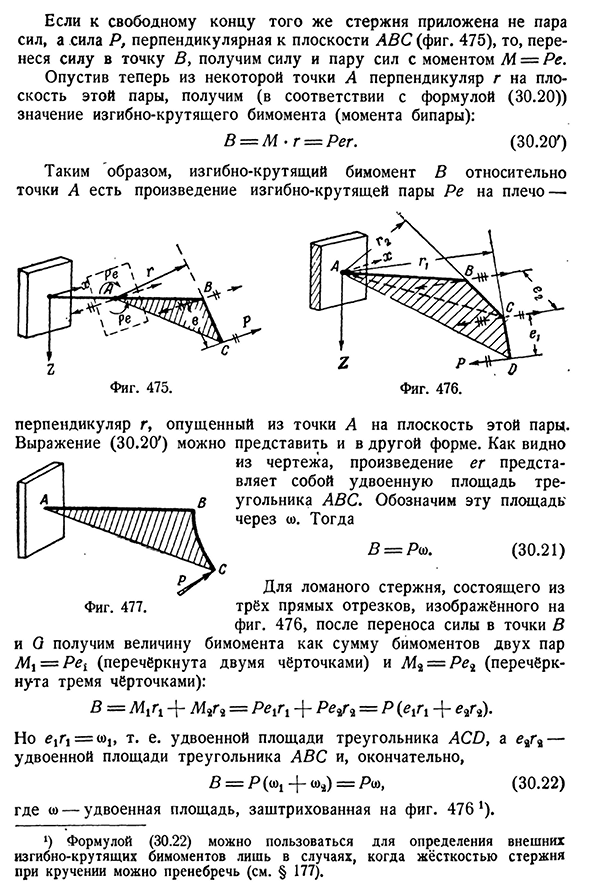
вариационный метод в строительной механике, ГТТИ, 1948.544 основа для расчета тонкостенных стержней[гл. XXX Если на свободный конец того же стержня приложена сила Р, перпендикулярная плоскости АВС, а не пара сил(рис. 475), то, если вы передадите силу в точку B, вы получите пару сила-сила в момент m=Re. Опуская перпендикуляр g из некоторой точки на плоскости этой пары, получаем величину изгибающего момента бимомента (бипара момент) (по формуле (30.20)): B=M-g=Reg. (30.20′) следовательно, бимомент изгиба-кручения B относительно точки A является произведением пары плеч изгиб-кручение PE — Фигура. 476. Перпендикуляры G падали из точки А в плоскость пары. Выражение (30.20′) может быть представлено в другой форме. Как видно из рисунков, произведением eg является площадь треугольника ABC в два раза. Эта область показана через o
). Затем 5=P (O. 30. 21) для сломанного стержня, состоящего из трех прямых сегментов, как показано на рисунке. 476, после передачи силы в точки B и G, мы получаем диморфное значение как сумму диморфных двух пар M x=PE±(пересеченных двумя черточками)и 2I2=RG2(три da (e ir I+e2g2). Но eghx=<oj, т. е. удвоенная площадь треугольника ACD, и удвоенная площадь восьмиугольного треугольника ABC, и, наконец, B=P (o) x4-<O2) = Ryu, (30.22) где») — 476 затененной области рисунка. да что с тобой такое? * ) Формула (30.22) может быть использована для определения внешних изгибных
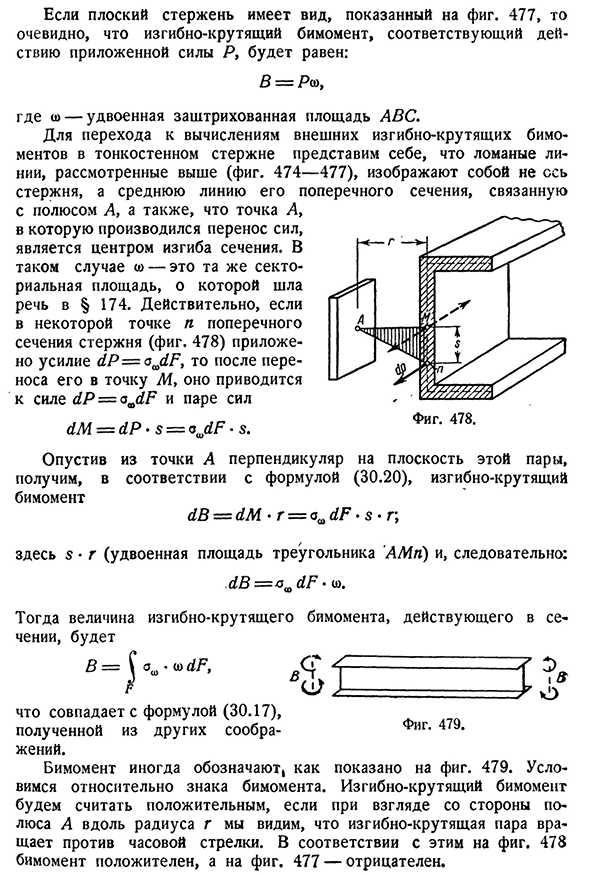
крутильных бимоментов только в том случае, если жесткостью на кручение стержня можно пренебречь (см.§ 177).§ 1751 сектор нормальное напряжение 545 Если плоский стержень имеет такую форму, как показано на рисунке. 477, очевидно, что бимомент изгиба-кручения равен приложенной силе, соответствующей действию Р: Б-Р® ) Где a) — заштрихованная область ABC. Чтобы перейти к расчету внешних изгибов-бимоментов кручения с тонкостенным стержнем, представим, что возможна ломаная линия в приведенном выше(рис. 474-477) представляет собой не ось стержня, а среднюю линию его поперечного сечения, соединенную с полюсом а, а также точку а, в которой осуществлялась передача сил, являющуюся центром изги
ба сечения. В этом случае W — та же площадь поперечного сечения, что и в пункте 174. Действительно, если в какой-то точке n поперечного сечения стержня(рис. 478) после приложения силы d P-s^dF и ее передачи в точку M она уменьшается до пары силы dP=aJiF и силы dM=dP-s-a JI•s. Фигура. 478. Опуская перпендикуляр к плоскости этой пары из точки А, получаем димер изгиба-кручения, согласно формуле (30.20 дБ-ДМ * Р=^ДФ•ы * г, Здесь s * g (удвоенная площадь треугольника усилителя) и, следовательно: d B-z^d F ’ io. Тогда стоит изгибать крутильные бимоменты, действующие
на поперечное сечение Это совпадает с формулой, полученной из других расчетов(30.17). Бимомент иногда появляется! Как использовать согласитесь на знаки 479 Bymoment. Бимомент изгиба кручения считается положительным, если видно, что пара изгиба кручения вращается против часовой стрелки при рассмотрении вдоль радиуса g от полюса A. согласно этому, 478bimoment является положительным и фиг. 477-отрицательно.
Смотрите также:

