С крепостной башни производят два выстрела, причем начальные скорости снарядов оказываются равными

Задача №47.

С крепостной башни производят два выстрела, причем начальные скорости снарядов оказываются равными по величине и лежат в одной и той же вертикальной плоскости. Эти начальные скорости направлены под углам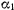и и 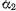к горизонту. Оба снаряда попадают в одну и ту же точку на поверхности Земли. Найти высоту башни, предполагая, что поверхность Земли вокруг башни горизонтальна и что сопротивление воздуха отсутствует.

Решение:

Уравнение траектории точки в общем случае движения под действием силы тяжести имеет вид

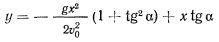
(ось 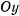предполагается направленной вертикально вверх). При разных значениях угла 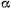по условиям задачи снаряды попадают в одну и ту же точку. Поэтому, исключая из двух уравнений траектории, получим

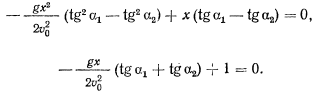
Тогда для 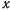будем иметь

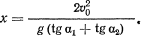
Здесь 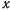— горизонтальная дальность до цели. Подставляя это значение в уравнение траектории, найдем высоту цели над башней

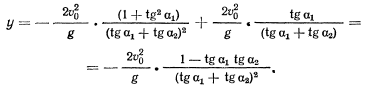
То есть высота башни равна

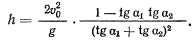
Задача взята со страницы подробного решения задач по всем темам теоретической механики:

Решение задач по теоретической механике

Возможно эти дополнительные задачи вам будут полезны:

Задача №44. Пусть ось направлена вертикально вверх. Будем предполагать, что на материальную точку действует только сила тяжести. Проекция силы тяжести на ось будет постоянна по величине и имеет отрицательное значение —. Поэтому движение материальной точки вдоль оси будет определяться дифференциальным уравнением.

Задача №45. Материальная точка массы притягивается неподвижным центром с силой , где — постоянный коэффициент пропорциональности, — расстояние точки от . В начальный момент расстояние , а скорость образует с направлением угол . Найти уравнения движения точки и ее траекторию, принимая прямую за ось .

Задача №49. Материальная точка массы описывает окружность радиуса , притягиваясь некоторой точкой этой окружности. Найти силу притяжения и скорость точки в зависимости от расстояния точки от .

Задача №48. Материальная точка описывает параболу под действием двух равных по величине сил, одна из которых направлена к фокусу параболы и обратно пропорциональна расстоянию точки от этого фокуса. Другая сила параллельна оси абсцисс и направлена в положительную сторону этой осн. Показать, что точка движется по параболе равномерно и определить величину скорости точки.