Оглавление:
Числовые ряды
Ряд
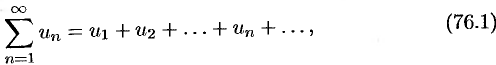
членами которого являются комплексные числа, называется числовым рядом (в комплексной области). Ряд (76.1) с комплексными членами 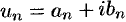 можно записать в виде
можно записать в виде
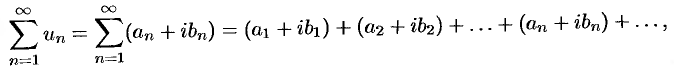
где 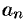 и
и 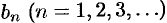 — действительные числа.
— действительные числа.
Сумма 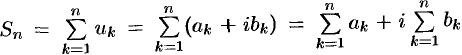 первых
первых  членов ряда (76.1) называется
членов ряда (76.1) называется  -й частичной суммой ряда.
-й частичной суммой ряда.
Если существует конечный предел  последовательности частичных сумм
последовательности частичных сумм 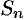 ряда:
ряда: 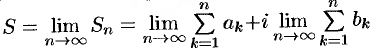 , то ряд (76.1) называется сходящимся, a
, то ряд (76.1) называется сходящимся, a  — суммой ряда; если
— суммой ряда; если 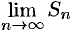 не существует, то ряд (76.1) называется расходящимся.
не существует, то ряд (76.1) называется расходящимся.
Очевидно, что ряд (76.1) сходится тогда и только тогда, когда сходится каждый из рядов
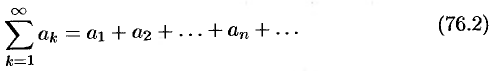
и
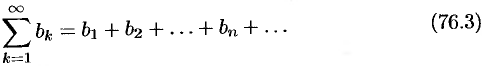
При этом 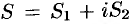 , где
, где 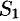 — сумма ряда (76.2), a
— сумма ряда (76.2), a 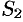 — сумма ряда (76.3). Это означает, что исследование сходимости ряда с комплексными членами сводится к исследованию сходимости рядов (76.2) и (76.3) с действительными членами.
— сумма ряда (76.3). Это означает, что исследование сходимости ряда с комплексными членами сводится к исследованию сходимости рядов (76.2) и (76.3) с действительными членами.
В теории рядов с комплексными членами основные определения, многие теоремы и их доказательства аналогичны соответствующим определениям и теоремам из теории рядов с действительными членами.
Приведем некоторые из них.
Остатком ряда (76.1) называется разность
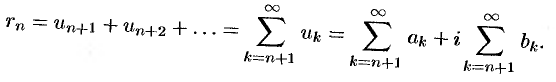
Теорема 76.1 (необходимый признак сходимости ряда). Если ряд (76.1) сходится, то его общий член 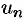 при
при 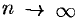 стремится к нулю:
стремится к нулю: 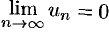 .
.
Ряд (76.1) называется абсолютно сходящимся, если сходится ряд
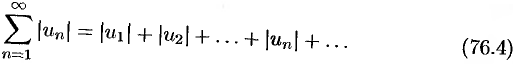
Теорема 76.2. Если сходится ряд (76.4), то абсолютно сходится ряд (76.1).
По условию ряд с общим членом 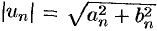 сходится. Тогда в силу очевидных неравенств
сходится. Тогда в силу очевидных неравенств 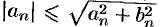 и
и  и на основании признака сравнения (теорема 60.1) сходятся ряды
и на основании признака сравнения (теорема 60.1) сходятся ряды 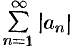 и
и 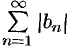 . Отсюда, следует сходимость рядов (76.2) и (76.3), а значит, и абсолютная сходимость ряда (76.1).
. Отсюда, следует сходимость рядов (76.2) и (76.3), а значит, и абсолютная сходимость ряда (76.1).
Если ряд абсолютно сходится и имеет сумму  , то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму
, то ряд, полученный из него перестановкой членов, также сходится и имеет ту же сумму  , что и исходный ряд.
, что и исходный ряд.
Абсолютно сходящиеся ряды можно почленно складывать и перемножать.
При исследовании на сходимость рядов с комплексными членами применимы все известные из действительного анализа признаки сходимости знакопостоянных рядов, в частности признак Даламбера: если существует 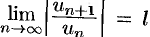 , то при
, то при 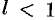 ряд (76.4) абсолютно сходится, а при
ряд (76.4) абсолютно сходится, а при 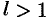 — расходится.
— расходится.
Степенные ряды
Степенным рядом в комплексной области называют ряд вида
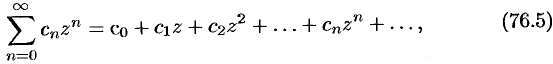
где 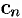 — комплексные числа (коэффициенты ряда),
— комплексные числа (коэффициенты ряда), 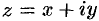 — комплексная переменная.
— комплексная переменная.
Рассматривают также и степенной ряд вида

который называют рядом по степеням разности 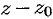 ,
,  — комплексное число. Подстановкой
— комплексное число. Подстановкой 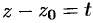 ряд (76.6) сводится к ряду (76.5).
ряд (76.6) сводится к ряду (76.5).
Ряд (76.5) при одних значениях аргумента  может сходиться, при
может сходиться, при
других — расходиться.
Совокупность всех значений  , при которых ряд (76.5) сходится, называется областью сходимости этого ряда.
, при которых ряд (76.5) сходится, называется областью сходимости этого ряда.
Основной теоремой теории степенных рядов является теорема Абеля, устанавливающая область сходимости степенного ряда.
Теорема 76.3 (Абель). Если степенной ряд (76.5) сходится при 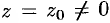 (в точке
(в точке  ), то он абсолютно сходится при всех значениях
), то он абсолютно сходится при всех значениях  , удовлетворяющих условию
, удовлетворяющих условию 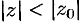 .
.
Доказательство теоремы аналогично доказательству теоремы Абеля в действительном анализе (теорема 63.1).
Следствие 76.1. Если ряд (76.5) расходится при 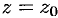 , то он расходится при всех значениях
, то он расходится при всех значениях  , удовлетворяющих условию
, удовлетворяющих условию 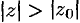 (т. е. вне круга радиуса
(т. е. вне круга радиуса 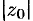 с центром в начале координат).
с центром в начале координат).
Из теоремы Абеля следует существование числа 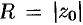 такого, что при всех значениях
такого, что при всех значениях  , удовлетворяющих неравенству
, удовлетворяющих неравенству 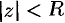 , степенной ряд (76.5) абсолютно сходится. Неравенству
, степенной ряд (76.5) абсолютно сходится. Неравенству 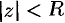 удовлетворяют точки комплексной области, лежащие внутри круга радиуса
удовлетворяют точки комплексной области, лежащие внутри круга радиуса 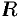 с центром в точке
с центром в точке 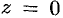 .
.
Величина 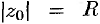 называется радиусом сходимости ряда (76.5), а круг
называется радиусом сходимости ряда (76.5), а круг 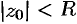 — кругом сходимости ряда. В круге
— кругом сходимости ряда. В круге 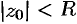 ряд (76.5) сходится, вне этого круга — расходится; на окружности
ряд (76.5) сходится, вне этого круга — расходится; на окружности 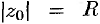 могут располагаться как точки сходимости, так и точки расходимости ряда.
могут располагаться как точки сходимости, так и точки расходимости ряда.
Принято считать, что 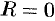 , когда ряд (76.5) сходится в одной точке
, когда ряд (76.5) сходится в одной точке 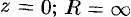 , когда ряд сходится на всей комплексной плоскости. Кругом сходимости ряда (76.6) является круг
, когда ряд сходится на всей комплексной плоскости. Кругом сходимости ряда (76.6) является круг 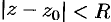 с центром в точке
с центром в точке 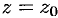 .
.
Радиус сходимости ряда (76.5) можно вычислить по формуле 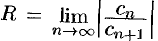 (или
(или 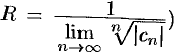 ), получаемой после применения признака Даламбера (или Коши) к ряду из модулей его членов исходного ряда.
), получаемой после применения признака Даламбера (или Коши) к ряду из модулей его членов исходного ряда.
Приведем (без доказательств) некоторые свойства степенного ряда.
- Сумма степенного ряда внутри круга его сходимости есть аналитическая функция.
- Степенной ряд внутри круга сходимости можно почленно дифференцировать и почленно интегрировать любое число раз. Полученный при этом ряд имеет тот же радиус сходимости, что и исходный ряд.
Пример №76.1.
Найти область сходимости ряда 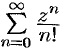 .
.
Решение: Здесь 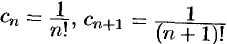 ,
,
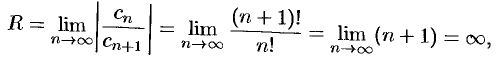
т. е. 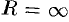 . Следовательно, областью сходимости является вся плоскость
. Следовательно, областью сходимости является вся плоскость  .
.
Пример №76.2.
Найти область сходимости ряда 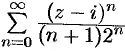 .
.
Решение:
Здесь 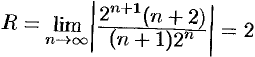 . Данный ряд сходится в области
. Данный ряд сходится в области 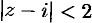 .
.
Дополнительный пример №76.3.
Ряд Тейлора
Теорема 76.4. Всякая аналитическая в круге 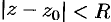 функция
функция  может быть единственным образом разложена в этом круге в степенной ряд
может быть единственным образом разложена в этом круге в степенной ряд
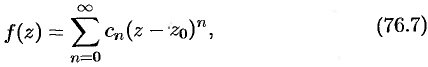
коэффициенты которого определяются формулами
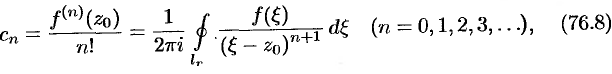
где 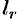 — произвольная окружность с центром в точке
— произвольная окружность с центром в точке  , лежащая внутри круга.
, лежащая внутри круга.
Степенной ряд (76.7) называется рядом Тейлора для функции  в рассматриваемом круге.
в рассматриваемом круге.
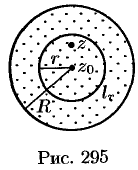
Возьмем произвольную точку  внутри данного круга и проведем окружность с центром в точке
внутри данного круга и проведем окружность с центром в точке  и радиусом
и радиусом 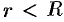 так, чтобы точка
так, чтобы точка  находилась внутри круга
находилась внутри круга 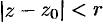 (см. рис. 295).
(см. рис. 295).
Так как функция  аналитична в круге
аналитична в круге 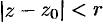 и на его границе
и на его границе 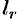 , то ее значение в точке
, то ее значение в точке  можно найти по формуле Коши (75.9):
можно найти по формуле Коши (75.9): 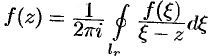 , где
, где 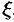 — точка на окружности
— точка на окружности 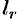 . Имеем:
. Имеем:
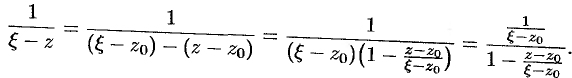
Так как 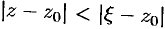 , то
, то 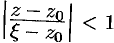 , следовательно, выражение
, следовательно, выражение 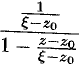 можно рассматривать как сумму членов бесконечно убывающей геометрической прогрессии с первым членом
можно рассматривать как сумму членов бесконечно убывающей геометрической прогрессии с первым членом 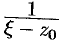 и знаменателем
и знаменателем 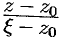 . Таким образом,
. Таким образом,
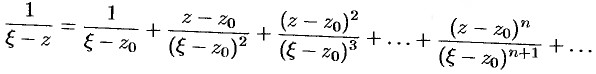
Умножим обе части этого равенства на величину 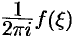 и проинтегрируем его почленно по контуру
и проинтегрируем его почленно по контуру 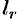 . Получим:
. Получим:
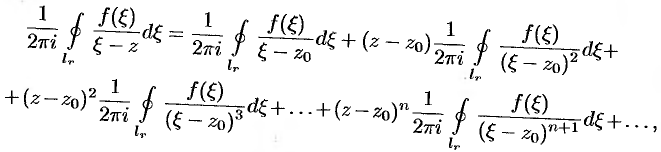
т. e. 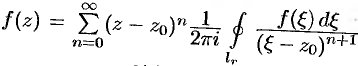 , или
, или 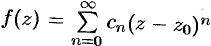 , где
, где 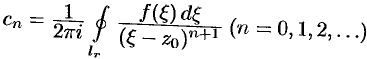 . Используя формулу (75.10), получим представление коэффициентов ряда через
. Используя формулу (75.10), получим представление коэффициентов ряда через  -е производные функции
-е производные функции  в точке
в точке  :
: 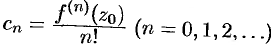 .
.
Таким образом, мы получили разложение функции  в степенной ряд (76.7), коэффициенты которого определяются по формулам (76.8).
в степенной ряд (76.7), коэффициенты которого определяются по формулам (76.8).
Докажем единственность этого разложения.
Допустим, что функция  в круге
в круге 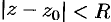 представлена другим степенным рядом
представлена другим степенным рядом
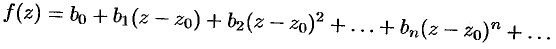
Последовательно дифференцируя почленно этот ряд бесконечное число раз, будем иметь:
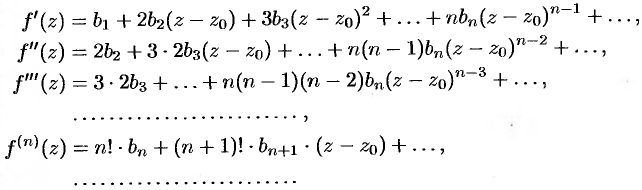
Полагая в этих равенствах, а также в исходном ряде 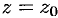 , получаем:
, получаем: 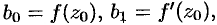
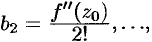
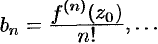 Сравнивая найденные коэффициенты
Сравнивая найденные коэффициенты 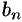 ряда с коэффициентами ряда (76.7), устанавливаем, что
ряда с коэффициентами ряда (76.7), устанавливаем, что  , а это означает, что указанные ряды совпадают.
, а это означает, что указанные ряды совпадают.
Функция  разлагается в степенной ряд единственным образом.
разлагается в степенной ряд единственным образом.
Приведем разложения некоторых элементарных функций в ряд Тейлора (Маклорена):
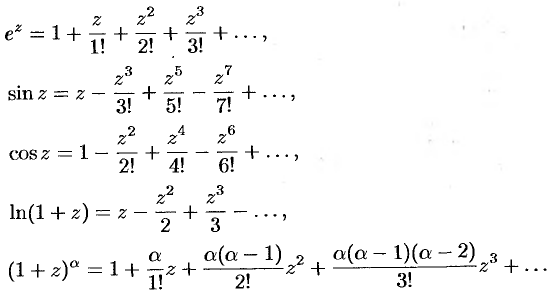
Первые три разложения справедливы во всех точках комплексной плоскости, последние два — в круге  .
.
Заменив  на
на 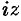 в разложении функции
в разложении функции 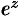 , получим:
, получим:
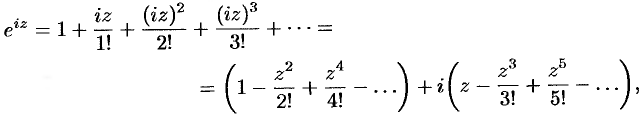
т. е. формулу Эйлера 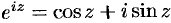 .
.
Дополнительная лекция: Нули аналитической функции
Ряд Лорана
Теорема 76.5. Всякая аналитическая в кольце 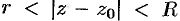
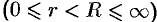 функция
функция  может быть разложена в этом кольце в ряд
может быть разложена в этом кольце в ряд
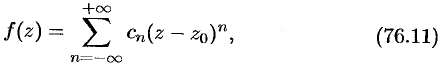
коэффициенты которого определяются формулой
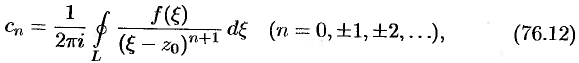
где  — произвольная окружность с центром в точке
— произвольная окружность с центром в точке  , лежащая внутри данного кольца.
, лежащая внутри данного кольца.
Рад (76.11) называется рядом Лорана для функции  в рассматриваемом кольце.
в рассматриваемом кольце.
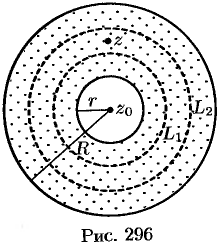
Возьмем произвольную точку  внутри кольца
внутри кольца 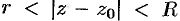 и проведем две окружности
и проведем две окружности 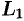 и
и 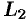 с центрами в точке
с центрами в точке  так, чтобы точка
так, чтобы точка  была между ними и каждая окружность находилась внутри данного кольца (см. рис. 296).
была между ними и каждая окружность находилась внутри данного кольца (см. рис. 296).
Функция  аналитична в кольце между окружностями
аналитична в кольце между окружностями 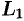 и
и 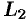 и на самих окружностях. Поэтому по формуле Коши для многосвязной области имеем:
и на самих окружностях. Поэтому по формуле Коши для многосвязной области имеем:
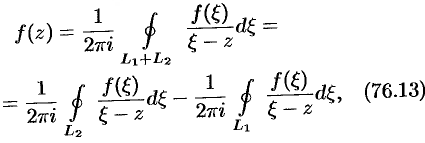
где обе окружности 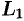 и
и 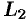 обходятся против часовой стрелки.
обходятся против часовой стрелки.
Преобразуем слагаемые, стоящие в правой части равенства (76.13), рассуждая, как и при выводе формулы Тейлора.
На окружности 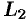 выполняется неравенство
выполняется неравенство 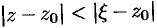 , или
, или 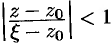 . Поэтому дробь
. Поэтому дробь 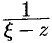 можно представить в виде
можно представить в виде
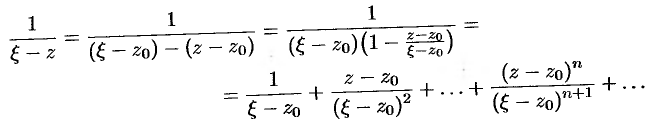
Тогда
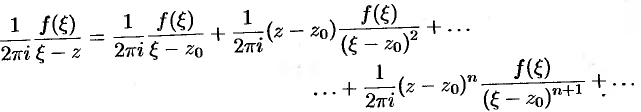
Проинтегрируем это равенство по контуру 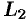 :
:
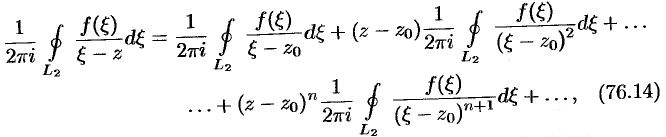
т.е. 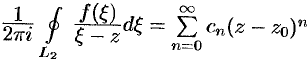 , где
, где
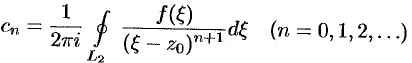
(здесь 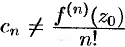 , так как функция
, так как функция  , возможно, не аналитична в точке
, возможно, не аналитична в точке  ).
).
На окружности 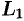 имеем
имеем 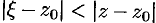 , т. е.
, т. е. 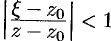 . Тогда
. Тогда
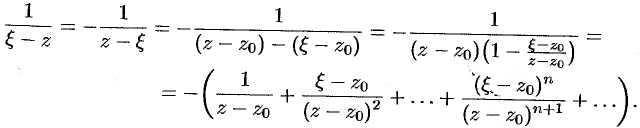
Значит,
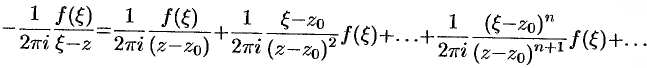
Проинтегрируем это равенство почленно по контуру 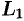 :
:
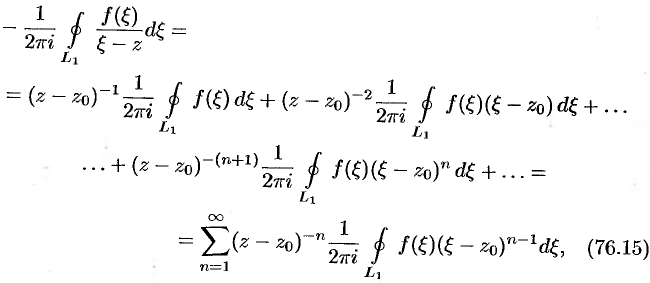
т.е. 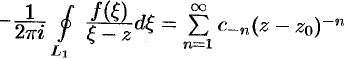 , где
, где
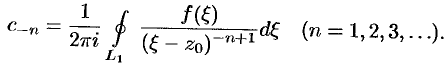
Подставив разложения (76.14) и (76.15) в равенство (76.13), получим
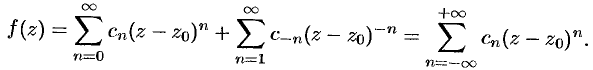
Формулы для коэффициентов 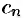 и
и 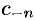 можно объединить, взяв вместо контура
можно объединить, взяв вместо контура 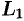 и
и 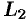 любую окружность
любую окружность  с центром в точке
с центром в точке  , лежащую в кольце между
, лежащую в кольце между 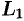 и
и 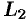 (следует из теоремы Коши для многосвязной области):
(следует из теоремы Коши для многосвязной области): 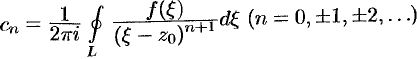 .
.
Можно доказать, что функция  , аналитическая в данном кольце
, аналитическая в данном кольце 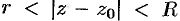 , разлагается в ряд Лорана (76.11) единственным образом.
, разлагается в ряд Лорана (76.11) единственным образом.
Ряд Лорана для функции
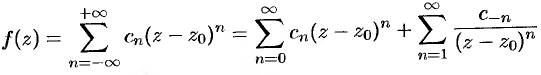
состоит из двух частей. Первая часть ряда Лорана, т. е. ряд
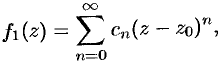
называется правильной частью ряда Лорана, этот ряд сходится к аналитической функции 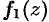 внутри круга
внутри круга 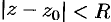 . Вторая часть ряда Лорана, т. е. ряд
. Вторая часть ряда Лорана, т. е. ряд
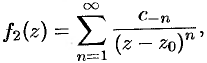
называется главной частью ряда Лорана; этот ряд сходится к аналитической функции 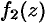 вне круга
вне круга 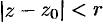 .
.
Внутри кольца 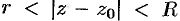 ряд
ряд 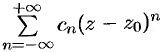 сходится к аналитической функции
сходится к аналитической функции 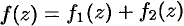 .
.
В частности, если функция  не имеет особых точек внутри круга
не имеет особых точек внутри круга 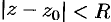 , то ее разложение в ряд Лорана обращается в ряд Тейлора.
, то ее разложение в ряд Лорана обращается в ряд Тейлора.
Замечание. На практике при разложении функции в ряд Лорана используют известные разложения основных элементарных функций; дробь вида 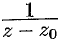 разлагается в ряд, являющийся рядом геометрической прогрессии; дробь вида
разлагается в ряд, являющийся рядом геометрической прогрессии; дробь вида 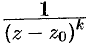 , где
, где 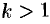 — целое, разлагается в ряд, который получается из ряда геометрической прогрессии последовательным дифференцированием
— целое, разлагается в ряд, который получается из ряда геометрической прогрессии последовательным дифференцированием 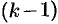 раз; сложная дробь представляется в виде суммы простейших дробей.
раз; сложная дробь представляется в виде суммы простейших дробей.
Пример №76.4.
Разложить в ряд Лорана функцию 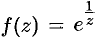 в окрестности точки
в окрестности точки 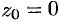 .
.
Решение:
Воспользуемся известным разложением
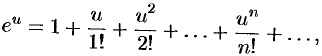
справедливым на всей комплексной плоскости. Положив 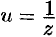 , получим
, получим
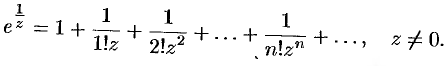
Дополнительный пример №76.5.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Предел и непрерывность функции комплексного переменного |
| Основные элементарные функции комплексного переменного |
| Понятие вычета и основная теорема о вычетах |
| Преобразование Лапласа |

