Оглавление:
Ряды Тейлора и Маклорена
Если функция 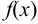 в некоторой окрестности точки
в некоторой окрестности точки 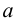 разлагается в степенной ряд
разлагается в степенной ряд
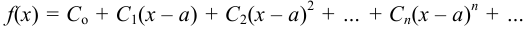
и имеет производные любых порядков, то коэффициенты этого ряда определяются по формулам:
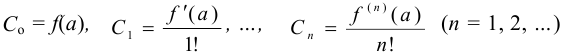
Степенной ряд
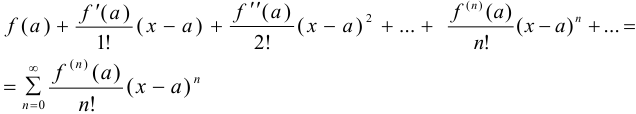
называется рядом Тейлора функции 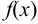 в точке
в точке 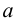 .
.
Если 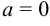 , то ряд
, то ряд
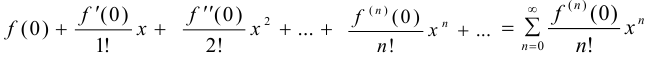
называется рядом Маклорена.
Достаточное условие разложения функции в ряд Тейлора
Теорема. Если функция 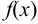 имеет производные любого порядка и они ограничены в окрестности точки
имеет производные любого порядка и они ограничены в окрестности точки 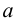 одним и тем же числом
одним и тем же числом 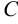 , т. е.
, т. е. 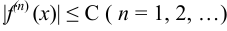 , то для любого
, то для любого 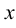 из этой окрестности выполняется равенство
из этой окрестности выполняется равенство
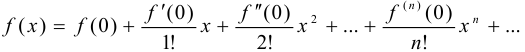
Рассмотрим разложение в степенной ряд (ряд Маклорена) некоторых элементарных функций:
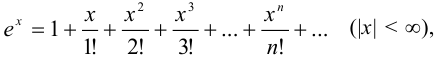
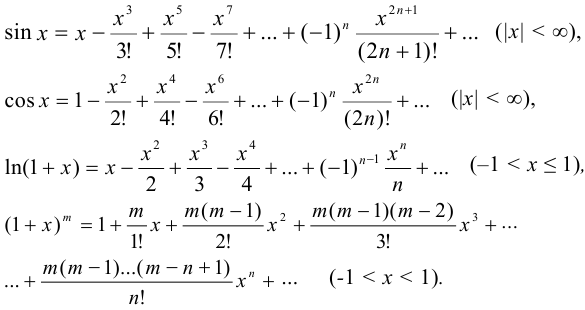
Задача №116.
Разложить в ряд Тейлора функцию 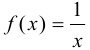 по степеням
по степеням 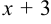
Решение:
Воспользуемся разложением
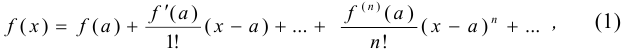
положив в нем 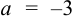 и вычислив значение производных этой функции при
и вычислив значение производных этой функции при 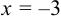 .
.
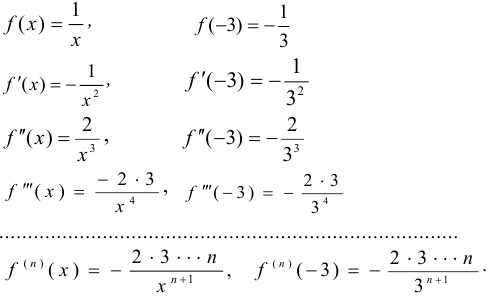
Подставим эти значения в формулу (1), получим
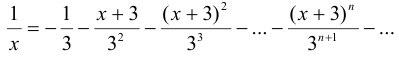
Этот ряд сходится, если 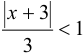 , т. е. при
, т. е. при 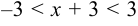 или
или 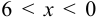 . Полученный степенной ряд является рядом Тейлора для функции
. Полученный степенной ряд является рядом Тейлора для функции 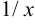 .
.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

