Оглавление:
В вопросах приложения теории рядов крайне важно уметь представлять данную функцию 
в виде суммы степенного ряда, т.е. разлагать функцию в степенной ряд.
Допустим, что функция разложена в степенной ряд в интервале сходимости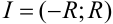 
: 
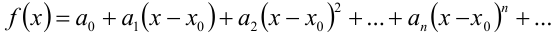
Выразим коэффициенты ряда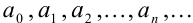 
через значения функции и её производных в точке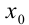 
.
Для этого, подставив в 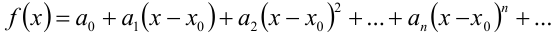вместо 
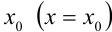, получим 
.
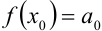По свойству степенных рядов (свойство 3 лекции 35), почленно продифференцируем наш ряд:
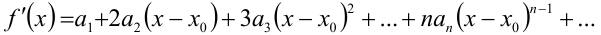
Подставив в это равенство вместо 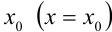, получим 
.
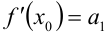Ещё раз применяя свойство степенных рядов, почленно продифференцируем ряд
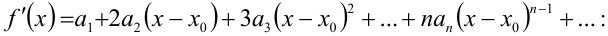
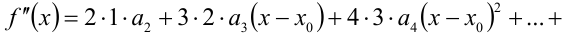
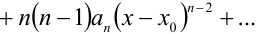
Подставив в это равенство вместо 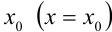, получим 
.
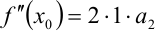Продолжая эти действия, будем иметь: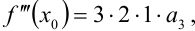 
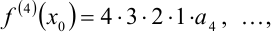
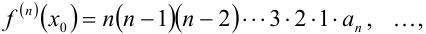или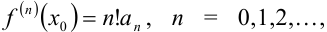 
где полагаем 
.
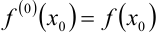Из данных формул определим значения коэффициентов 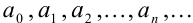ряда
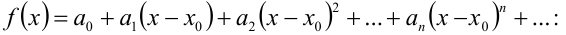
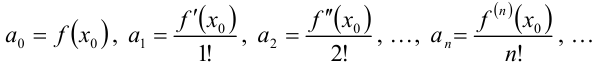
Подставив значения коэффициентов в наш ряд, получим:
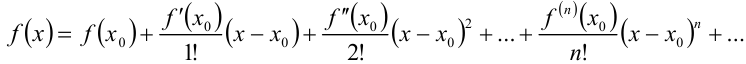
Ряд называется рядом Тейлора для функции в точке .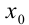
Ряд Тейлора для функции в точке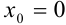 
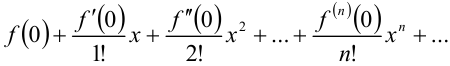называется рядом Макларена.
Если функция имеет в точке 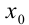производные любого порядка, то для неё можно составить ряд Тейлора или ряд Маклорена. При этом функция называется порождающей функцией для соответствующего ряда.
Пример №36.1.
Найдите третий член ряда Маклорена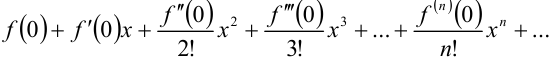 
для функции 
.
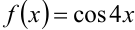Решение:
Третий член ряда Маклорена для функции имеет вид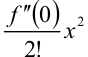 
. Для его нахождения вычислим вторую производную функции 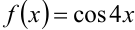в точке :
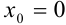1) найдём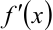 
: 
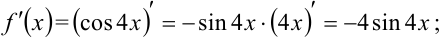
2) найдём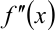 
:
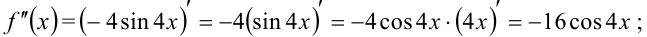
3) найдём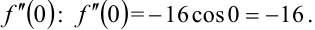 
Подставим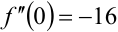 
в выражение 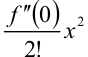, получим: 
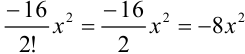. Таким образом, третий член ряда Маклорена для функции 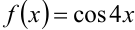равен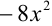 
.
Ответ: .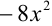
Пример №36.2.
Составьте ряд Маклорена для функции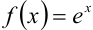 
.
Решение:
Ряд Маклорена для функции имеет вид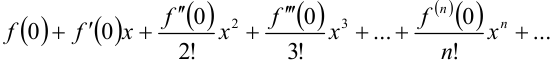 
Составим его для функции 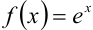. Для этого найдём значения функции 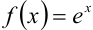и последовательно её производных в точке :
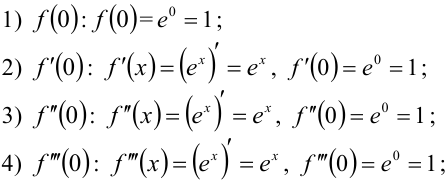
Поскольку для функции 
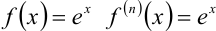, то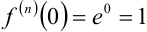 
.
Подставим найденные значения в формулу ряда Маклорена и получим:
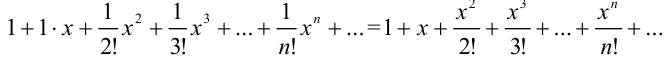
Таким образом, функция 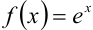порождает следующий ряд Маклорена
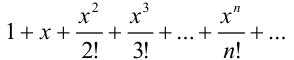
Ответ: функции 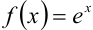сопоставляется ряд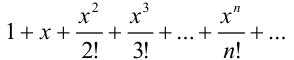
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Область сходимости степенного ряда. |
| Свойства степенных рядов. |
| Разложение элементарных функций в ряд. |
| Практическое применение разложений функций в ряд. |
