Оглавление:

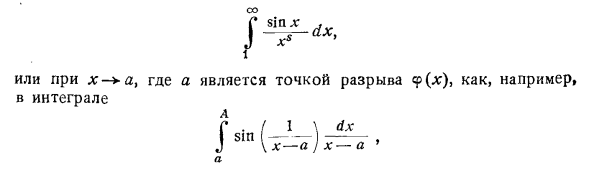
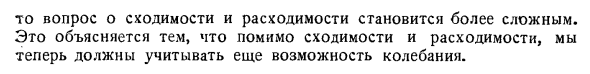
Ряды, содержащие положительные и отрицательные члены
- Строка, содержащая положительные и отрицательные элементы. Определение суммы бесконечных рядов и несоответствующих интегральных значений обоих типов 1 и 2 применимо к интегрированию в рядах, где члены могут иметь любой знак и функции, которые меняют знак в интервале интегрирования. Я могу Тем не менее, специальные признаки сходимости или расхождения, установленные в первой части этой главы, и примеры, которые их описывают, являются почти исключительными для рядов с только положительными или отрицательными членами и функциями, которые не меняют знак в интервале интегрирования.
При рассмотрении ряда мы всегда предполагаем, иногда предписываем это, а иногда подразумеваем, что условия, наложенные на s, могут не выполняться для конечного числа членов. Людмила Фирмаль
Примеры решения, формулы и задачи
| Решение задач | Лекции |
| Расчёт найти определения | Учебник методические указания |
- Это было связано в порядке. Вам нужно только начать с определенного термина и того, что такое условие (например, термин является положительным) выполнено. Аналогично, в случае неправильного интегрирования условие выполняется для всех значений x, превышающих значение π, или для всех значений x из определенного интервала (a, a -) — B, который включает в себя значение a Предполагалось, что Уменьшить).
Так, например, наши знаки можно применять к следующим сериям: n> -10 В случае n ^ 4, n1-10 ^> 0. От 1 / 3х-7. f 1-2 * л 7 1 Если x>, 3x-7> 0, если 0, 1-2x> 0 <n: <j. Но независимо от того, насколько велико n, то есть знак не меняется как в положительном, так и в отрицательном выражении Например, серия 1-3-4 ‘ Или φ (x) Или как x- + a, где a — разрыв (X), например, интегралПроблемы конвергенции и расхождения являются более сложными.
Это связано с тем, что в дополнение к сходимости и расхождению необходимо учитывать возможность вибрации. Людмила Фирмаль

