Оглавление:

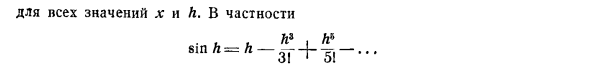




Ряд Тейлора
- Серия Тейлор. Предположим, что f (x) имеет производные всех порядков в интервале (a-m), a + ttj), содержащих точку * = a. Тогда, если h является абсолютным и меньше, чем tj, f (a + K) = f (a) + hf (a) + … + £ 2X) + ^ f / <«> (» + 0 „Л), Где 0 <^ Ol <1 для всех n. Или, л — 1 о Далее идет: f (a + h) -Sn = Rn. Также предположим, что po это O. тогда / (A + Λ) = ш $$, = / («) + * / ()) + — £ — / + …. Л — ОО Это разложение / (a + ‘0 известно под названием ряда Тейлора. Если a = 0, выражение принимает вид: / (A) = / (0) + hf (0) + -g- / ‘(0) + .. Так называемая серия Магслорена.
Читатель должен знать о ложном мнении о том, что существование всех производных функции / (а) является достаточным условием для справедливости расширения функции ряда Тейлора. Поведение Rn важно. (1) Линии знака и косинуса. f (*) = грех младший Тогда f (x) имеет производные всех порядков всех значений x. Кроме того, l / ^ ArJj-Cl для всех значений x и n. Так что в этом случае хн ^ «‘^ LU» стремится к 0 PR «l- ♦ (см. Пример XXVII.12), независимо от значения h. h * L5 h4 грех (x -f L) = грех x -f h, потому что x-sin x- ^ cosjr-j- ^ sin x -f -…
Функция Rn называется формой Лагранжа остаточного члена. Людмила Фирмаль
Для всех значений х и L. особенно Я » L3 I L * sin L = h s | N «5i ••• Для всех значений Л. Точно так же, La l3 cos (l: -f L) = cos l: -L sin l: — ^ cos x ^ sin l: 4 … и , La, L4 (2) Биноминальный ряд. Пусть f (x) = (1 + f) n. Где m — любое положительное или отрицательное рациональное число. тогда F (α) (-) = m (m-1) … (m ~ n + 1) (1 + x) ™ -и и ряды маклаурина (с заменой A на л;) Если m — положительное целое число, последовательность прерывается и получается известная биноминальная теорема с положительными целыми показателями.
Общий случай Hn = / / <«> (9n *) = («) Xy (1 + eХX) м, И чтобы показать, что ряд Маклаурина действительно представляет (I — \ — x) m в области со значением x, если m не является положительным целым числом, то Rn- для всех значений * этой области Должен показать ‘0. На самом деле это делается с -1 m и (^ j xn-0η-ω (например, xxvii.13), но -1 1, если n> m. Зная только 0 <0 „<1 1, нельзя подтвердить, что 1 не очень мало, (1 4-вялг) м-н очень большой. Чтобы доказать биномиальное разложение с помощью теоремы Тейлора, нам нужно использовать другое представление остаточного члена Rnt, рассмотренное ниже (раздел 167).
| Длины плоских кривых | Касание плоских кривых |
| Теоремы о среднем высших порядков | Касание n-го порядка |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Применение теоремы Тейлора. А. Высокий и низкий. Теорема Тейлора может быть использована для получения систем с полными и минимальными знаками, которые являются более полными, чем те, которые обсуждались в этом параграфе. 123 и 124. Однако эти результаты не очень практичны.
l. = $: Максимум i> ‘(5) = 0,9 «(S) <0; минимум 9’ (S) = 0, 9 * Очевидно, что эти символы не применяются в этом случае 9 ‘и 9 «(E) равны нулю. Предположим, что 9 (x) имеет n производных 9 «, » (), (*).
В предположении, что 9 (*) имеет первые два порядка производной, мы установили следующее достаточное условие, чтобы 9 (l) имело максимальное или минимальное значение Людмила Фирмаль
Из них все, кроме последнего, исчезает с x =%. Далее (2) с. Согласно 151, + =? <«> © + Oy> Выражение также должно иметь постоянный знак для максимального или минимального значения, когда положительное или отрицательное значение h достаточно мало. Это, очевидно, требует, чтобы n было четным. Если n — четное число, максимальное или минимальное значение получается в зависимости от того, является ли φ (n) (S) отрицательным или положительным.
Таким образом, получается следующее предложение: если cp (£) является максимальным или минимальным, минимальная производная, которая не исчезает при x =, должна быть четным числом, а если значение в этой точке является отрицательным, 9 (S ) Максимум, и если он положительный, 9 (5) — минимум. Пример. LVIL. 1. Проверьте справедливость теоремы для функции cos * —1, cos * —1 + ^ |» cos * l ~ f «2T if» *** ‘
Некоторые предельные расчеты. Если аргумент принимает определенное значение и обе функции исчезают, часто необходимо вычислить предел отношения двух функций. Предположим, что значение аргумента ^ равно 0. Существует несколько способов расчета таких пределов. (A) Предположим, что f (x) и 9 (.k) дифференцируемы при x = 0, а f (0) = 9 (0) = 0, 9 ‘(0) 0,0. / () = Xf (0) + o (x), 9 () = x9 ‘(0) + o (x) Таким образом, / () ./ ‘(0) )? ‘(0)’ В общем, если функция имеет x производных с x = 0, и первые n-1 производных каждой из этих функций инвертированы В этот момент он становится равным нулю, 9 (л) (0)> 0, а затем Sec. Согласно теореме 151, f (* > = / / ЛЛ) (°) + 0 < «> •.» <>: = £? (H) (°) + 0 ( «)

