Оглавление:
Ряд геометрической прогрессии
Исследуем сходимость ряда
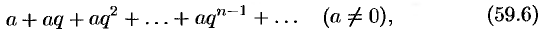
который называется рядом геометрической прогрессии. Ряд (59.6) часто используется при исследовании рядов на сходимость.
Как известно, сумма первых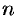 
членов прогрессии находится по формуле 
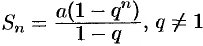. Найдем предел этой суммы:
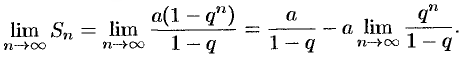
Рассмотрим следующие случаи в зависимости от величины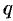 
:
- Если
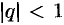, то 
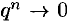при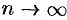 
. Поэтому 
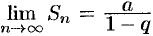, ряд (59.6) сходится, его сумма равна 
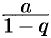. - Если
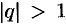, то 
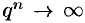при 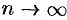. Поэтому 
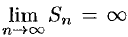, ряд (59.6) расходится; - Если
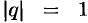, то при 
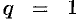ряд (59.6) принимает вид 
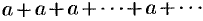, для него 
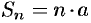и 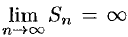, т. е. ряд (59.6) расходится; при 
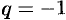ряд (59.6) принимает вид 
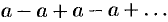— в этом случае 
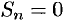при четном 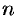и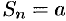 
при нечетном 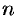. Следовательно, 
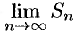не существует, ряд (59.6) расходится.
Итак, ряд геометрической прогрессии сходится при 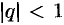и расходится при 
.
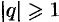Пример №59. 1.
Показать, что ряд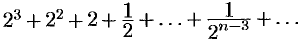 
сходится.
Решение:
Данный ряд можно переписать так:
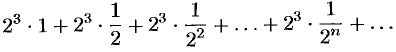
Как видно, он представляет собой ряд геометрической прогрессии с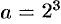 
и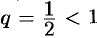 
. Этот ряд сходится согласно свойству 1 числовых рядов.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Метод вариации произвольных постоянных ЛНДУ |
| Интегрирование нормальных систем |
| Необходимый признак сходимости числового ряда |
| Достаточные признаки сходимости знакопостоянных рядов |
