Оглавление:
Разложение в ряд Фурье 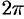 -Периодических функций
-Периодических функций
Теорема Дирихле
Выясним условия, при которых знак соответствия (~) можно заменить знаком равенства (=), т. е. условия, при которых ряд Фурье функции  сходится и имеет своей суммой как раз функцию
сходится и имеет своей суммой как раз функцию  .
.
Будем рассматривать функции  , имеющие период
, имеющие период 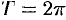 . Такие функции называют
. Такие функции называют 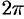 -периодическими.
-периодическими.
Сформулируем теорему, представляющую достаточное условие разложимости функции в ряд Фурье.
Теорема 67.1 (Дирихле). Пусть 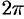 -периодическая функция
-периодическая функция  на отрезке
на отрезке 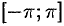 удовлетворяет двум условиям:
удовлетворяет двум условиям:
 кусочно-непрерывна, т. е. непрерывна или имеет конечное число точек разрыва I рода;
кусочно-непрерывна, т. е. непрерывна или имеет конечное число точек разрыва I рода; кусочно-монотонна, т. е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.
кусочно-монотонна, т. е. монотонна на всем отрезке, либо этот отрезок можно разбить на конечное число интервалов так, что на каждом из них функция монотонна.
Тогда соответствующий функции  ряд Фурье сходится на этом отрезке и при этом:
ряд Фурье сходится на этом отрезке и при этом:
- В точках непрерывности функции сумма ряда
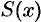 совпадает с самой функцией:
совпадает с самой функцией: 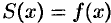 ;
; - В каждой точке
 разрыва функции сумма ряда равна
разрыва функции сумма ряда равна 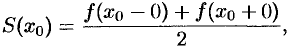
т. е. равна среднему арифметическому пределов функции справа и слева;
справа и слева; - В точках
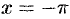 и
и 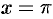 (на концах отрезка) сумма ряда равна
(на концах отрезка) сумма ряда равна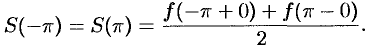
Таким образом, если функция  удовлетворяет условиям 1 и 2 теоремы (условия Дирихле), то на отрезке
удовлетворяет условиям 1 и 2 теоремы (условия Дирихле), то на отрезке 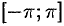 имеет место разложение (66.12):
имеет место разложение (66.12):
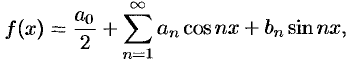
причем коэффициенты вычисляются по формулам (66.13) — (66.15). Это равенство может нарушиться только в точках разрыва функции  и на концах отрезка
и на концах отрезка 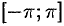 .
.
В силу периодичности исходной функции и суммы ряда Фурье может быть получено указанное разложение во всей области определения функции.
Замечания.
- Если функция
 с периодом
с периодом 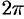 на отрезке
на отрезке 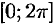 удовлетворяет условиям Дирихле, то для нее имеет место разложение (66.12), где коэффициенты вычисляются по формулам
удовлетворяет условиям Дирихле, то для нее имеет место разложение (66.12), где коэффициенты вычисляются по формулам 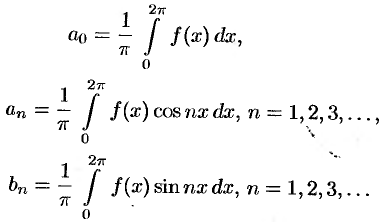
(Интегралы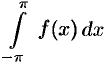 и
и 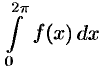 равны в силу свойства 3 периодической функции — см. п. 66.1.)
равны в силу свойства 3 периодической функции — см. п. 66.1.) - Условиям Дирихле удовлетворяют большинство функций, которые встречаются в математике и ее приложениях. Существуют функции, не удовлетворяющие условиям Дирихле, по при этом разложимые в ряд Фурье, т. е. теорема Дирихле дает лишь достаточное условие разложимости, но не необходимое.
Пример №67.1.
Разложить в ряд Фурье функцию  периода
периода 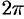 , заданную на отрезке
, заданную на отрезке 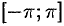 формулой
формулой
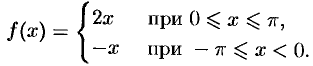
Решение:
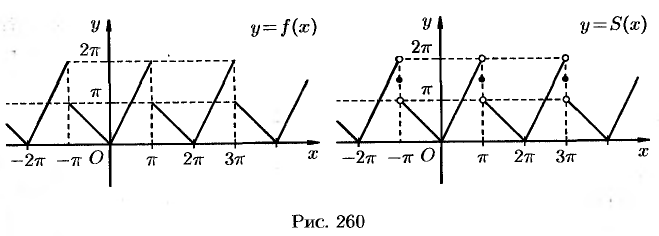
На рисунке 260 изображен график функции  . Эта функция удовлетворяет условиям Дирихле, значит, она разложима в ряд Фурье. Находим коэффициенты ряда:
. Эта функция удовлетворяет условиям Дирихле, значит, она разложима в ряд Фурье. Находим коэффициенты ряда:
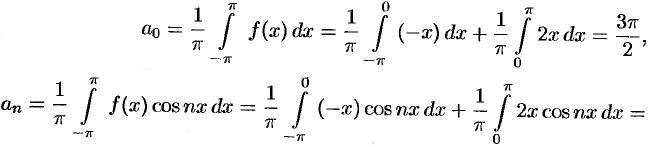
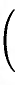 интегрируем по частям:
интегрируем по частям: 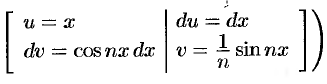
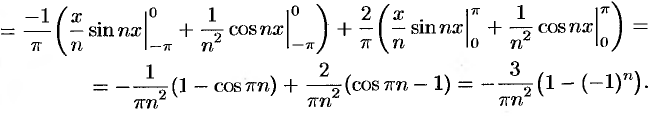
Аналогично находим
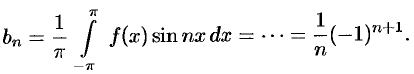
Исходной функции  соответствует ряд Фурье
соответствует ряд Фурье
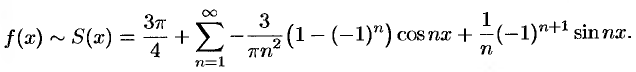
Функция  непрерывна во всех внутренних точкой отрезка
непрерывна во всех внутренних точкой отрезка 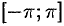 , поэтому, согласно теореме Дирихле, для всех этих точек имеем равенство
, поэтому, согласно теореме Дирихле, для всех этих точек имеем равенство 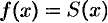 , т. е.
, т. е.
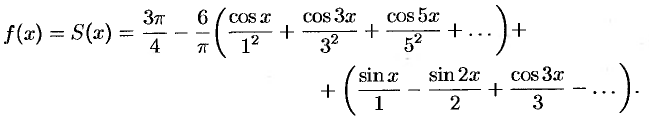
В точках 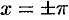 сумма
сумма 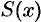 ряда равна
ряда равна
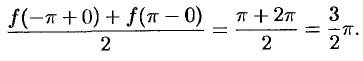
Графики функций  и
и 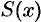 показаны на рис. 260.
показаны на рис. 260.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Ряды Тейлора и Маклорена |
| Периодические функции. Периодические процессы |
| Поверхности и линии уровня скалярного поля |
| Производная по направлению скалярного поля |

