Оглавление:






Роль поверхностного натяжения при образовании новой фазы. Зародыши
- Проблема фазового перехода обсуждалась ⧧ 36-40 без учета поверхностной энергии. Поэтому сделанные там выводы актуальны, если граница раздела фаз очень плоская (малая кривизна).Однако в большинстве случаев, поскольку происходит фазовый переход, 1 из фаз образуется в мелкодисперсной форме (образование жидкости из пара в виде мелких капелек тумана, осаждение мелких кристаллов из расплава, образование пузырьков при кипении жидкости и т. д.).
В системах мелкодисперсной формы отношение поверхности к объему очень велико, поэтому энергия поверхности может играть важную роль. Описывая его, можно объяснить многие явления, происходящие во время, например, конденсации паров, кристаллизации и др. Рассмотрим переход из парового состояния в жидкое, образование капель жидкости в этой паре жидкостей. Найти равновесное состояние размещенных капель(рис. 11).
От этой зависимости зависит термодинамика по потенциалу от радиуса падения получается следующий вывод. Людмила Фирмаль
Состояние системы определяется давлением temperature. To найдя равновесное состояние, необходимо изучить термодинамический потенциал Φ (p, T; p, v>, m.) (см. 5 36) и найти его минимальное значение с учетом свободной поверхности energy. In в этом случае термодинамический потенциал Это дается путем Ф= в + ПВ = + п «» я)+ как. (3.85> y,, v> — массовая и Удельная) и 2-я (парообразная) фазы соответственно. dav§ § 35-40, это считается внешним параметром. /,- /, (у»Г) и f,=Т) являются специфическими свободными энергиями. S — площадь поверхности капли. а-поверхностное натяжение на границе раздела фаз.
Поверхностное натяжение a является функцией T, которая, строго говоря, является функцией y и y₂.Однако он не учитывает зависимости a от y и yg. Капли будут сферическими. Это основано на равновесном состоянии, когда требуется минимальное значение условия, и когда форма капли изменяется на постоянную mₕy, у₂.Тогда только термин aS изменяется на in, и минимальное значение of соответствует сферическому shape. In в этом случае поверхность S минимизируется для заданного объема капли.
Здесь в качестве независимого внутреннего параметра задачи, который необходимо изменить при нахождении равновесия, можно предположить, что величины YY и m, остальные величины (масса 2-й фазы m, радиус капли H и ее поверхность S) связаны равенством: — m» 4L/ 3 = m «4L / 3», YL =5L = m. Для того чтобы описать условия равновесия, необходимо найти производные Φ для y, y и приравнять их к нулю. Различный г > с точки зрения Фи、 (3.86> (3.87> Это тривиальное следствие.
Давление пара равно давлению поршня. Различают фи по определенному объему капель. = 0. (3.88> Поэтому давление в капле р не равно р, а наоборот Р1 =товар итого+ (3.89} Вычислите 2-й член. dvJdR = 4л / t₁, так/ ДС \ нам 1 ДСМ 2ми ojm, ««» я 4la2, 9С А-Р Нед⁺’ ПЛ = П + ^- (3.90)) (3.91)) (3.92)) Последняя формула показывает, что на границе раздела 2 фаз (капель и паров) происходит скачок давления, равный 2a / H. Здесь мы оставляем P и V constant постоянными и изменяем m. это соответствует переходу жидкости из капли в пар или наоборот versa. It следует отметить, что этот процесс испарения и конденсации происходит с участием диффузии и значительно дольше, чем процесс выравнивания давления.
Если мы различаем Пхи-м、 «/1 + ПВИ-фут-pvₜ+ (3.93) граф ДС / дмэ. _ ds’Dr___________ как П、_ „М (ду ^ / д),^ — dR₄яД“ „я• Такой образ. (3.94)) (3.95) Удельный термодинамический потенциал жидкости будет введен Pa“ ’f, (p» G)=/,.(pTT)+ P. P,. ψ (ptt)= f,(pГT)+ pi> I. А затем… (3.96)) Кроме того, выполняются условия равновесия dF / d0,= 0 и dF / doc =» = 0、 (3.97) Для краткости опишите fDrc T), а не fDr.). Существует пересыщенный пар, p> p, (7′), а давление насыщенного пара p является условием φ (p.- FDr»)), то есть оно определяется равновесием на плоской границе раздела фаз.
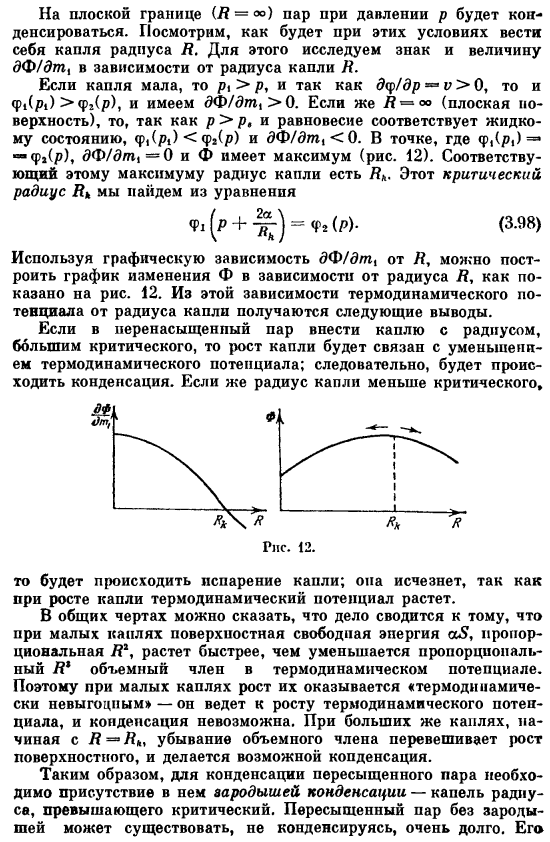
На плоской границе(H=») пар конденсируется под давлением p. посмотрим, как работает капля радиуса под этими conditions. To сделайте это, изучите знак и величину dF / dt, в зависимости от радиуса падения. Если капля маленькая, то п> р, д р / д-> 0, т. е. φ|(Р») > φ»(Р), ДФ / ДМ> 0. = = p> p, для = σ(плоскость), и 平 (β₁)φα (P) и DF / dm,0, поскольку равновесие соответствует жидкому состоянию. Др — — Ф (1 (p), DF / dm = 0 и в точке, где φ становится максимумом (рис.12).
- Радиус падения, соответствующий этому максимальному значению, равен I этот критический радиус выражения. Используя графическую зависимость dF / dt от, мы можем построить график изменения Φ в зависимости от радиуса, как показано на рисунке 5. 12. Если, кроме критического пара, к пересыщенному добавляются капли с радиусом, то эти капли связаны с уменьшением термодинамического потенциала. Следовательно, произойдет конденсация. Радиус падения меньше критического.
Потом капелька evaporates. As капли растут, их термодинамический потенциал увеличивается, в результате чего Опа исчезает. В общем виде задачу можно суммировать тем, что поверхностная свободная энергия as, пропорциональная H2, растет быстрее объемного члена, пропорционального термодинамическому потенциалу H *в малых drops. So, при малых каплях их рост «термодинамически невыгоден» -приводит к увеличению термодинамического потенциала, соосаждение невозможно.
Здесь возможно метастабильное состояние 1 фазы, а появление другой фазы требует наличия ядра, которое больше критического. Людмила Фирмаль
Для крупных капель, начинающихся при R = R, уменьшение объемного члена превышает рост поверхностного члена, и происходит конденсация. Итак, для конденсации пересыщенного пара в нем должно быть ядро конденсации-капли радиуса, превышающего критический. Пересыщенный пар без ядра может существовать очень долго без конденсации. Его (3.99) Состояние является примером метастабильного состояния.
Рассчитайте критический радиус падения. если p мало-p «Пи Р1)= Ф1 (Р)+ тят(Пи-П). И g p, / dr = p,, p, — p = 2aJR, так、 ₽я(Пи)= 4> (р) (3.100) Уравнение критического радиуса I можно записать в виде: 1 (п) — ФГ(П)=- (3.101) (3.102) Предположим, что перенасыщение мало, иpDp>) ’ ■ = Pi (p.) и подумайте、 Джей>ₜ(п) — пр(.p)=(v₂-1″|) (p, — p). В этом случае уравнение для R * принимает вид: (П * — » и) (п-п.)- (3.103) (3.104) Откуда? (3.105) Из этого уравнения видно, что критический радиус пропорционален поверхностному натяжению.
Знаменатель терминов(.р-п. А) указывает на то, что чем выше пересыщение пара, тем меньше а, и, соответственно, тем быстрее он начинает конденсироваться. Аналогичное условие справедливо для всех переходов 1-го порядка. При испарении жидкой массы, роль этих ядер играют пузырьки пара, а при кристаллизации из жидкости кристаллов. Качественно, в случае кристаллизации, ситуация такая же, как и в случае конденсации пара.
Для более точного решения, вообще говоря, следует учитывать, что энергия свободной поверхности равна месту, где существует суммирование, так как поверхностное натяжение Кристалла отличается в разных его сторонах Он обнаруживается вдоль всех граней кристалла(S-площадь i-й грани, а поверхност-поверхностное натяжение I-й грани). Отметим, что роль ядер в конденсации и кристаллизации могут играть не только капли или кристаллы определенных веществ, но и частицы посторонних частиц(пыль).
Они играют эту роль, если поверхностное натяжение границы между инородным телом и рассматриваемой жидкостью в случае конденсации значительно меньше, чем граница между жидкостью и ее поверхностью. vapor. In в свою очередь, такие частицы, покрытые лишь тонким слоем жидкости, ведут себя как капли жидкости одинакового размера, вызывая конденсацию.
Поэтому для того, чтобы получить переохлажденный пар или переохлажденную жидкость, необходимо освободить вещество от пыли и удалить пыль, которая попадает в сосуд посредством предварительной очистки и использования герметичных емкостей. С помощью этих мер предосторожности можно, например, переохлаждать воду или другие жидкости на десятки градусов, доводя их до очень вязкого стеклянного состояния.
Смотрите также:
| Критическая точка | Конденсация электрически заряженных капель |
| Поверхностная энергия и поверхностное натяжение | Фазовые переходы второго рода. Точка Кюри ферромагнетика |

