Оглавление:






Результаты аналитического решения
- На основе аналитического решения задачи можно найти температурное поле при нестационарном теплопередаче. Рассмотрим расчетную зависимость, полученную аналитическим методом, на примере плоской стенки, в которой размеры вдоль Y-и z-осей очень велики, а теплопередачей от торцов можно пренебречь. Предположим, что условия теплопередачи от обеих поверхностей одинаковы. В этом случае температурное поле симметрично середине стенки, поэтому его толщину удобно выразить в 26 (рис. 4.3).
Разность температур (приведенная к плоской стенке в предыдущей записи 4.1) 1-мерная задача, учитывающая принятые уравнения избыточности 1-го порядка На поверхности граничные условия (4.10)) Временное условие: при m = 0 0 = 0 ′. Эта проблема решается путем разделения переменных. Обозначим искомую функцию 0 в виде произведения переменной T (m) и X (x).Первая функция зависит только от времени, вторая — только от координат (4.12) Дифференцируя это уравнение、 • = * — =Т— * а * ⁹ Ах ДХ, ДХ Ах, dhgAh2. Если вы назначите выражение E1 gi выражению(4.10), вы получите: О, да.
Прежде чем заняться таким расчетом, необходимо вывести дифференциальное уравнение, описывающее энергетические зависимости в движущейся среде. Людмила Фирмаль
Где pa-константа разделения переменных. Из Формулы (4.13) получаем 2 дифференциальных уравнения. Эй!: ^ + ₽ ₽ ’Т = 0; (4.14) 5 + ₽ ^ =ок. (4.15)) Известное решение Т = Ле — „’ “ \(4.16) X = vs VSO5 ₽ х + szshrh. (4-17) (4.12) по этим формулам учитывается、 0 =(С, потому что ПВ ЦС 3 ПХ) Е〜 » Р \(4.18) Из-за симметрии температурного поля, x не может быть заменен на — — — x Значение 0 должно быть отражено. Это условие является、 C,= 0, поэтому решение уравнения (4.18) сводится к следующему виду: Tso5rh 0 = Ce_av ’. (4.19)) Значение константы разделения переменных r 13 G Личные требования.
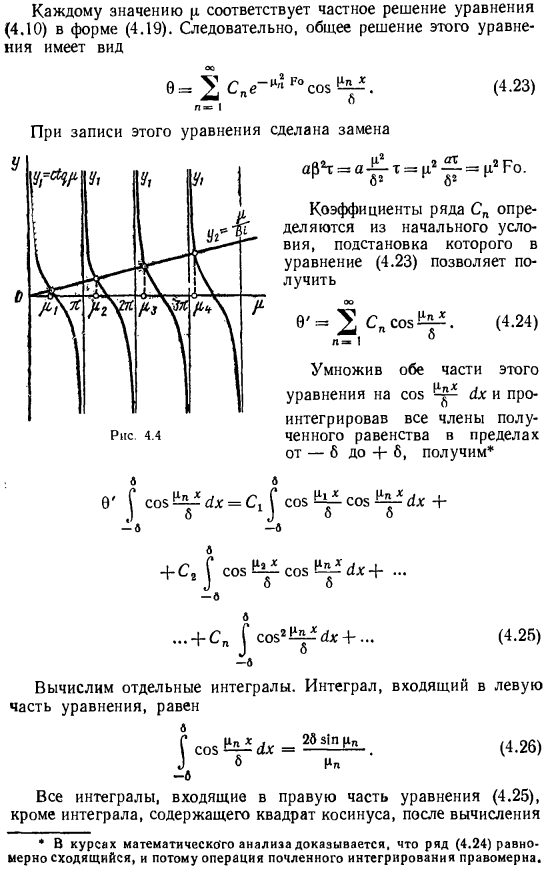
Вы можете легко найти его по формуле x =±6 (4.19) ’= 4.20) 0SH = Ce_oB не потому, что РБ. (4.21) Подставляя эти выражения в условие (4.11), получим: rz1prb = ^ sobrb (4.22) с-РБ; B1_ =А. На каждом значении числа B! Бесчисленные корни трансцендентального уравнения(4.22) (Ts1, pg, Tsa -.- ) Соответствует. Это уравнение обычно решается графически(рис. 4.4), и различные значения P В B1 суммируются в таблице.
Каждому значению Q соответствует определенное решение формулы вида (4.19) (4.10).Таким образом, общая форма решения этого уравнения является 9 = 2 Spe — » Roz Soz Vd2 (4.23) При написании этого уравнения производятся замены Коэффициенты ряда Cn определяются из начальных условий и присваиваются формуле (4.23).、 9 ’= 2 (⁴- 24) Умножим обе стороны этого уравнения на cos Bd ^ 4x и интегрируем все члены полученного уравнения в диапазоне от-b до 4-b, получим*. потому что б ^ 1, потому что bd2 в:4х + + С| / в COS Б ^ потому что б | 5 4×4— … +С «на соз» Е154х+ …(4.25 )) Вычислите индивидуальные интегралы.
Интеграл в левой части уравнения потому что 4х = 2 ^ «Б» ..в (4.26) Все интегралы в правой части уравнения(4.25), за исключением интегралов, содержащих квадрат вычисленного Косинуса •В процессе математического анализа доказано, что ряд (4.24) сходится равномерно, поэтому операция консолидации по термам обоснована. Получается ноль. Интегралы, содержащие квадрат Косинуса, определяются по формуле (4.27) Если мы подставим Интеграл (4.26) и (4.27) в уравнение (4.25)、 (4.28) Учитывая это уравнение, уравнение (4.23), отражающее распределение температуры в пластине, имеет вид、 (4.29) (4-30) Где x = x / 6. На рисунке показана форма температурного поля, соответствующая уравнению (4.30). 4.3.
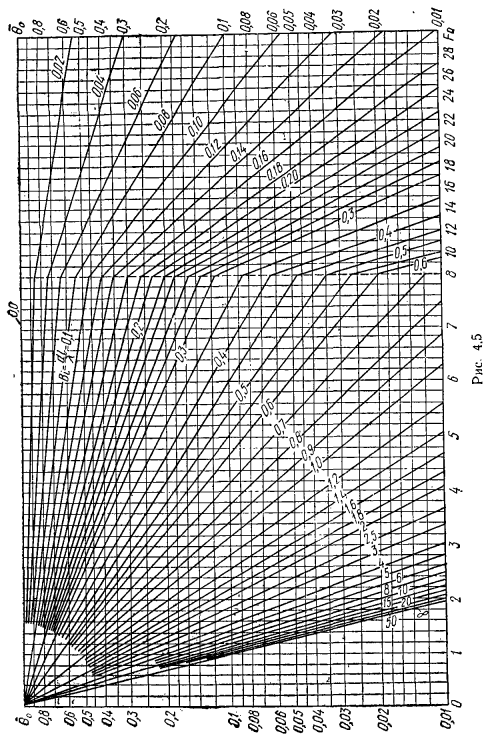
Использование полученных уравнений на практике связано с необходимостью выполнения трудоемких расчетов. Поэтому, используя эту формулу, строится график 6 = /(Ео, В1.*). (4.31) С его помощью вычисление будет очень простой операцией. Каждый график создается с помощью x = const. Наиболее широко используемые графики в библиографии-это графики x = 0 и x = 1. Каждый из них характеризует температуру плоскости симметрии и стороны стенки, но есть также график с x =■0.2. 0,4; 0,6; 0,8 [271.Рисунок 4.5 показывает это Зависимость при * = 0. Из рисунка 4.5 B 100 видно, что температура стенок перестает зависеть от условий теплообмена на границе тела.
- Это связано с тем, что в данном случае тепловое сопротивление внешней теплопередачи непропорционально мало по сравнению с внутренним сопротивлением. Поэтому температурное поле определяется условиями распространения тепла в теле. Количество тепла, которое получает или отдает стена, также определяется числом Eo и B’1.
Количество тепла, потерянного (или полученного)» (когда температура тела и температура среды равны), иТепло отдается в Т С другой стороны, если плотность материи равна p и стена теплая, вы можете написать: C) ’=26рс (г -/.) = 26рс0’、 (2X =26рс (г-1т) = 26ро (0 ′ — 0т)、 Где 1t-средняя температура стенки через определенный промежуток времени Если разделить терм на 2-е уравнение в терминах по первому уравнению, то получится: В каждый момент времени температурное поле стенок определяется числовыми значениями Eo и B|, поэтому средняя температура стенок зависит только от них figures. So … (4.32) График этой функции доступен в справочнике.
Оно поэтому может быть использовано для процессов теплообмена, в которых перепады температур таковы, что действительное изменение свойств невелико. Людмила Фирмаль
Иногда вместо этой функции приводится зависимость от средней безразмерной температуры стенки 0м = /(Ео, Б! это не. (4.33) Расчетное соотношение теплопроводности плоской стенки в нестационарных условиях получено при симметричных условиях теплообмена на обеих стенках. Эти соотношения могут быть использованы в обычных случаях несимметричных условий теплопередачи, когда одна из стен изолирована, а другая 1 участвует в теплопередаче transfer. In в этом случае расчетная толщина стенки b заменяется фиктивной стенкой толщиной 26(Рис. 4. 6), и все пропорции, полученные выше, применяются.
Температура в симметричной плоскости фиктивной стенки будет равна температуре адиабатической поверхности фактической стенки. Аналогичное решение задачи теплопередачи в температурном поле и нестационарных условиях теплопередачи, а также график, облегчающий их использование, доступно для бесконечно длинных цилиндров и шариков. Радиус выбирается как характерный размер этих тел. Аналитическое уравнение, определяющее температурное поле бесконечно длинного непрерывного цилиндра и непрерывного шара, имеет следующий вид: 0 = 2Р⁰ * ⁽3⁵⁾ Где Uo и — функции Бесселя нулевого и первого порядка типа 1. / ? = / ?// ?»• Значение P для цилиндра и шара определяется уравнением. И затем (4.36)) / xc1br = 1-Б1.
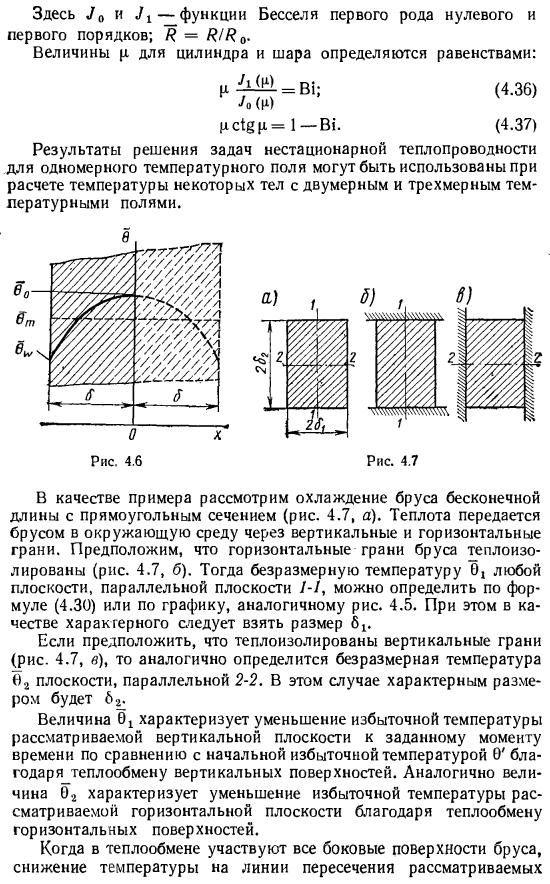
Результаты решения задачи нестационарной теплопроводности 1-мерного температурного поля можно использовать для расчета температуры некоторых 2D и 3D объектов. В качестве примера рассмотрим охлаждение балки бесконечной длины с прямоугольным поперечным сечением (рис.4.7, а).Тепло передается в окружающую среду через вертикальные и горизонтальные поверхности с помощью стержней. Предположим, что горизонтальный конец дерева изолирован (рис. 4.7, б).Тогда безразмерная температура 0°любой плоскости, параллельной плоскости 1-1, может быть определена с помощью графика, такого как формула (4.30) или Рисунок 3.
В то же время, размер 6p должен использоваться в качестве характеристики Если предположить, что вертикальная плоскость изолирована (рис. 4.7, в), то безразмерная температура δ плоскости, параллельной 2-2, определяется как well. In в этом случае характерный размер составит 6 г. Значение 0!По сравнению с начальной избыточной температурой 0 ′, обусловленной теплообменом вертикальной плоскости, она характеризуется снижением избыточной температуры рассматриваемой вертикальной плоскости до определенной точки. Аналогично, величина 0 g характеризует падение избыточной температуры рассматриваемой горизонтальной плоскости за счет теплообмена горизонтальной плоскости.
Понижение температуры на пересечении тепла, если все стороны древесины участвуют в теплопередаче Плоскость определяется одновременным воздействием теплопередачи на вертикальные и горизонтальные поверхности. Поэтому безразмерная температура этой линии равна произведению безразмерной температуры, которая определяется отдельно для теплообмена вертикальной и горизонтальной поверхностей. б =0₁ёё>>. (4.38) Таким образом, вы можете определить температуру в любой точке коробки-пересечение 3 planes. In в этом случае необходимо определить 3 безразмерные температуры, используя методику бесконечной плоской стенки, и безразмерная температура в рассматриваемой точке будет равна произведению.
При оценке температуры внутри цилиндра ограниченной длины безразмерная температура поверхности цилиндра заданного радиуса определяется по закону бесконечно длинных цилиндров и закону плоскости, параллельной дну цилиндра, по формуле температурного поля пластины, толщина которой равна длине цилиндра. Безразмерная температура на пересечении цилиндрической поверхности и плоскости равна произведению безразмерной температуры каждой из этих поверхностей. Приведенный выше метод известен как теорема умножения решения.
Смотрите также:

