Задача 1.47.
Решить модифицированным симплексным методом задачу 1.41, состоящую в определении максимального значения функции
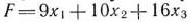
при условиях
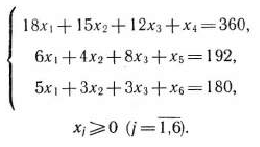
Решение:
Данная задача имеет опорный план
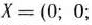
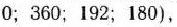
который определяется базисом, образованным векторами
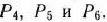
Компоненты этих векторов определяют единичную матрицу 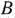 , обратная к которой
, обратная к которой 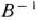 также является единичной.
также является единичной.
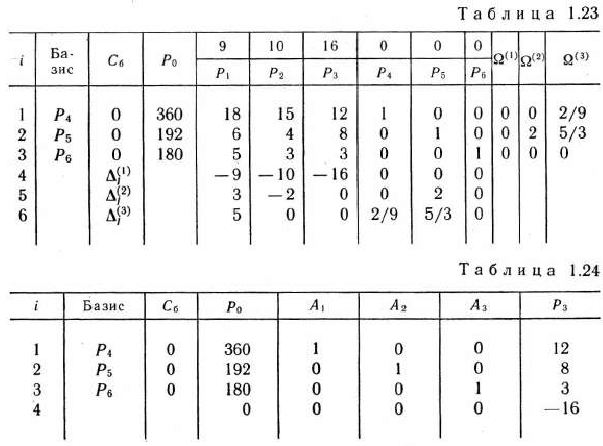
Составляем вспомогательную и основную таблицы (табл. 1.23 и 1.24). Сначала в табл. 1.23 на основе исходных данных заполняем первые три строки столбцов векторов 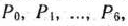 , а в табл. 1.24 —первые три строки столбцов векторов
, а в табл. 1.24 —первые три строки столбцов векторов 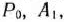
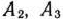 (элементы столбцов векторов
(элементы столбцов векторов 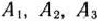 представляют собой соответствующие столбцы матрицы
представляют собой соответствующие столбцы матрицы 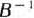 ). После этого находим вектор компоненты которого запишем в 4-й строке табл. 1.23. Эти числа определяем по формуле (38), т.е. получаем в результате скалярных произведений вектора
). После этого находим вектор компоненты которого запишем в 4-й строке табл. 1.23. Эти числа определяем по формуле (38), т.е. получаем в результате скалярных произведений вектора 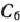 на соответствующие векторы
на соответствующие векторы 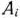 :
:
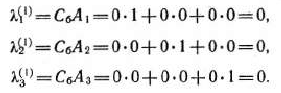
В 4-й строке табл. 1.24 в столбце вектора 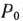 записано также значение целевой функции задачи при исходном опорном плане, которое получено как результат скалярного произведения вектора
записано также значение целевой функции задачи при исходном опорном плане, которое получено как результат скалярного произведения вектора 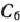 на вектор
на вектор 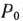 :
:
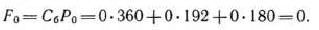
После заполнения 4-й строки табл. 1.24 найденные компоненты вектора 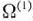 записываем в табл. 1.23, На основе данных этой таблицы по формуле (39) находим числа
записываем в табл. 1.23, На основе данных этой таблицы по формуле (39) находим числа 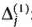 :
:
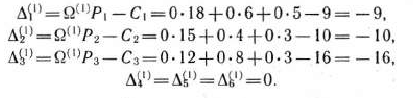
Так как среди чисел 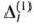 имеются отрицательные, то исходный опорный план не является оптимальным. Перейдем к новому опорному плану. Вектор, который при этом следует ввести в базис, определяют по наибольшей абсолютной величине отрицательных чисел
имеются отрицательные, то исходный опорный план не является оптимальным. Перейдем к новому опорному плану. Вектор, который при этом следует ввести в базис, определяют по наибольшей абсолютной величине отрицательных чисел 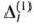 . В данном случае это число— 16, которое находится в столбце вектора
. В данном случае это число— 16, которое находится в столбце вектора 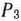 табл. 1.23. Поэтому последний столбец табл. 1.24 отводим для вектора
табл. 1.23. Поэтому последний столбец табл. 1.24 отводим для вектора 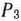 . В этом столбце записываем компоненты разложения вектора
. В этом столбце записываем компоненты разложения вектора 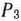 по векторам данного базиса. Они определяются в результате умножения матрицы
по векторам данного базиса. Они определяются в результате умножения матрицы 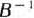 (записанной в табл. 1.24) на матрицу-столбец, элементами которой являются компоненты вектора
(записанной в табл. 1.24) на матрицу-столбец, элементами которой являются компоненты вектора 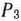 (записанные в табл. 1.23):
(записанные в табл. 1.23):
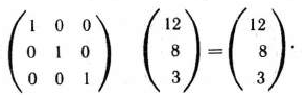
Если бы среди найденных чисел не было положительных, то задача не имела бы оптимального плана. Поскольку положительные числа имеются, переходим к новому опорному плану. Для этого введем в базис вектор 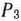 , а исключим из него вектор
, а исключим из него вектор 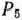 . Вывод из базиса вектора
. Вывод из базиса вектора 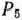 обусловлен тем, что
обусловлен тем, что
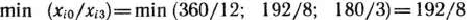
достигается при 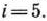
Считая теперь число 8 разрешающим элементом, а 2-ю строку и столбец вектора 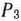 табл. 1.24 — направляющими, переходим к табл. 1.25, в которой элементы первых трех строк столб-
табл. 1.24 — направляющими, переходим к табл. 1.25, в которой элементы первых трех строк столб-
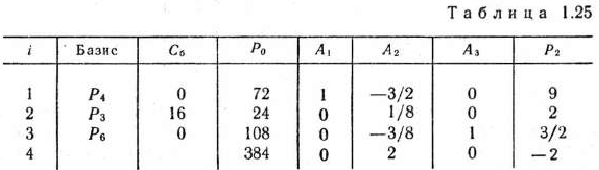
цов векторов 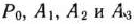 и найдены с помощью известных правил перехода от одной симплекс-таблицы к другой. После этого находим компоненты вектора
и найдены с помощью известных правил перехода от одной симплекс-таблицы к другой. После этого находим компоненты вектора 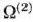 . Их значения получаются в результате скалярного произведения вектора
. Их значения получаются в результате скалярного произведения вектора 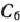 и соответствующих векторов
и соответствующих векторов 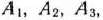 , компоненты которых записаны в табл. 1.25:
, компоненты которых записаны в табл. 1.25:

Полученные компоненты вектора 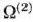 записываем в 4-й строке табл. 1.25 и в соответствующем столбце табл. 1.23. После этого находим числа
записываем в 4-й строке табл. 1.25 и в соответствующем столбце табл. 1.23. После этого находим числа 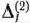 и записываем их в 5-й строке таблицы. Так как среди чисел есть отрицательное
и записываем их в 5-й строке таблицы. Так как среди чисел есть отрицательное 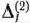 , то найденный опорный план
, то найденный опорный план
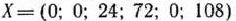
не является оптимальным. Поэтому в табл. 1.25 отводим последний столбец для вектора 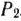 . Его компоненты в новом базисе определяются в результате умножения матрицы
. Его компоненты в новом базисе определяются в результате умножения матрицы 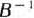 (элементами которой являются числа табл. 1.25, стоящие в столбцах векторов
(элементами которой являются числа табл. 1.25, стоящие в столбцах векторов 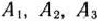 ) на матрицу-столбец, элементами которой являются компоненты вектора
) на матрицу-столбец, элементами которой являются компоненты вектора 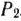 (записанные в табл. 1.23):
(записанные в табл. 1.23):
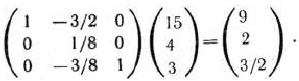
Найденные числа записываем в столбце вектора 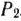 табл. 1.25. Так как среди этих чисел имеются положительные, то переходим к новому опорному плану (табл. 1.26). Это достигается введением в базис вектора
табл. 1.25. Так как среди этих чисел имеются положительные, то переходим к новому опорному плану (табл. 1.26). Это достигается введением в базис вектора 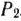 и исключением из него вектора
и исключением из него вектора 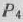 .
.

После заполнения первых трех строк табл. 1.26 вычисляем, как и выше, компоненты вектора 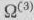 записываем их в 4-й строке табл. 1.26 и в соответствующем столбце табл. 1.23. Затем вычисляем числа
записываем их в 4-й строке табл. 1.26 и в соответствующем столбце табл. 1.23. Затем вычисляем числа 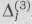 . Эти числа записаны в 6-й строке табл. 1.23. Так как среди них нет отрицательных,то найденный опорный план
. Эти числа записаны в 6-й строке табл. 1.23. Так как среди них нет отрицательных,то найденный опорный план
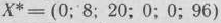
является оптимальным. При этом плане целевая функция задачи принимает свое максимальное значение

Эта задача взята со страницы решения задач по предмету «математическое программирование»:
Примеры решения задач по математическому программированию
Возможно эти страницы вам будут полезны:

