Оглавление:



Решения простейших уравнений теплопроводности для условий стационарного режима
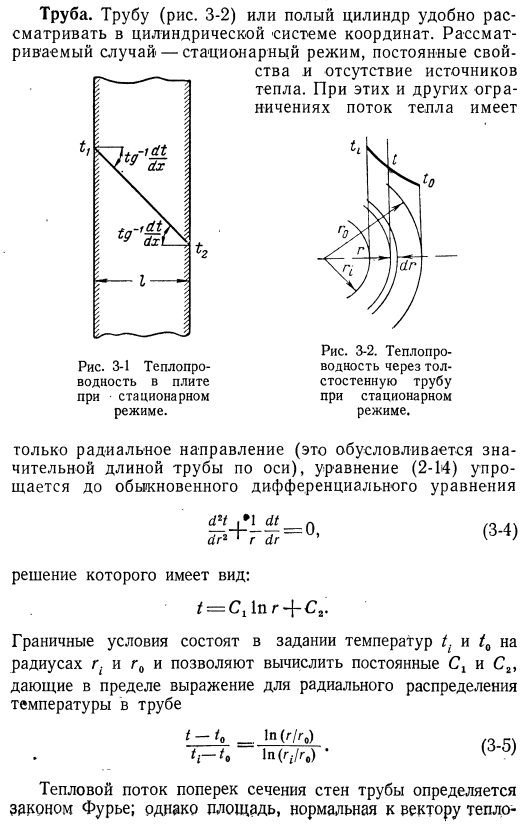
- Теплопроводность в стационарном состоянии Режим Для тел простой формы, таких как стенки, полые трубы и полые шары, уравнение теплопроводности значительно упрощается, если тепло постоянно распространяется в 1 измерении. * Плоские стенки (пластины); в плоской стенке(рис.3-1) с постоянной теплопроводностью толщиной I и бесконечной длиной другого измерения тепловой поток в этой области фактически равен 1 измерению.
Поэтому такие объекты удобно отображать в ортогональной системе координат. Если на стенке нет источника тепла, а тепловой поток стационарный и 1-мерный, то формула (2-13) принимает вид: (3-1) Решение: Т = Cₜx-C₂. Константы C и C₂ могут быть вычислены из граничных условий, определяющих температуры поверхности x = 0 и x = 1.Используйте эти условия для получения уравнения распределения температуры стенки. Тепловой поток через стенку можно получить из закона теплопроводности Фурье. Г_ _ Г ^ 2 / ЛЯ.• (3-3).
Энергия, которую получает или теряет тело в процессе теплообмена с окружающей средой, называется коли́чеством теплоты́ или просто теплотой. Людмила Фирмаль
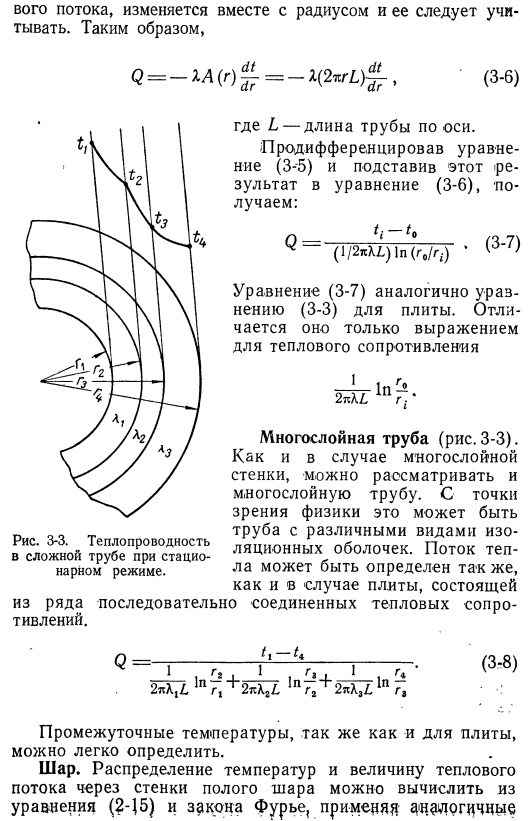
Поэтому и здесь уместно отметить совпадение в виде совпадения с обычным законом Ома (3-3). / Термин / LD соответствует электрическому сопротивлению, поэтому его называют термическим сопротивлением или термическим сопротивлением. The pipe. It удобно рассматривать полый цилиндр с трубой (рис. 3-2) или цилиндрическую систему координат. Рассматриваемый случай является стационарным режимом и является постоянным Рис. 3-1 * теплопроводность печи в стационарном режиме. уств и отсутствие источника тепла. При этих и других ограничениях тепловой поток составляет Рисунок 3-2.
- Теплопроводность толстостенных труб в стационарном режиме. Только в радиальном направлении(это зависит от важной длины трубы вдоль оси) формула (2-14) упрощается до обычных дифференциальных уравнений а Г2* /•доктор—» 1 (3-4) Форма его решения выглядит следующим образом: =₁₁1пг -} — ^ 2. Граничное условие находится в настройке температуры. Радиуса R и R/и пневмония Т-ТП(Фо) tᵢ-tlnln(РЗ / r₀) ’ Тепловой поток по сечению стенки трубы определяется законом Фурье. Однако площадь перпендикулярна теплу Поток, в зависимости от радиуса, должен быть учтен. Подобный этому М = — м (р) г.=- я(2wL)Дж Рисунок 3-3.
Теплопроводность сложной трубы в стационарном режиме. Где L — длина оси трубы. Если мы дифференцируем уравнение (3-5) и подставим этот результат в уравнение (3-6), то: ГВ (1/2 «Л1) 1П(г,/ г;) * ⁽3′ ⁷ ⁾ Формула (3-7) аналогична формуле плиты (3-3).Отличается только формула термического сопротивления Многослойные трубы(рис. 3-3); так же как и многослойные стенки, можно рассматривать многослойные трубы. С точки зрения физики, это будет труба с различными типами изолирующих оболочек. Тепловой поток можно определить так же, как и в случае с плитой От серии сопротивления жары соединенных последовательно.
Внутренняя энергия термодинамической системы может изменяться двумя способами: посредством совершения работы над системой и посредством теплообмена с окружающей средой. Людмила Фирмаль
Также, как плита, промежуточную температуру можно легко определить. Мяч. Можно ли рассчитать распределение температуры и величину теплового потока через стенку полого шара по уравнению (2-J5) и закону Фурье? Аналогичное приложение Такие предположения, как в случае с плитами и трубами. Распределение температуры получается таким образом Мы найдем тепловой поток отсюда. Н.—__ В. (1 / 4nL) [(1 / год)-(1 /год)] ’ (3-10) Формулу составного шара можно легко найти таким же образом, как из Формулы (3-10) в Формулу (3-8).
Смотрите также:
| Основной закон теплопроводности | Уравнение теплопроводности |
| Конвективный теплообмен граничных поверхностей | Критическая толщина изоляции |

