Оглавление:
Решение задачи на треугольник
Задача №18.
Даны координаты вершин 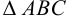 :
:  (1; 1),
(1; 1), 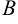 (7; 4),
(7; 4), 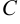 (4; 5). Найти: 1) длину стороны
(4; 5). Найти: 1) длину стороны  ; 2) уравнение стороны
; 2) уравнение стороны  ; 3) уравнение медианы
; 3) уравнение медианы  ; 4) внутренний угол
; 4) внутренний угол  ; 5) координаты точки пересечения высот. Сделать чертеж.
; 5) координаты точки пересечения высот. Сделать чертеж.
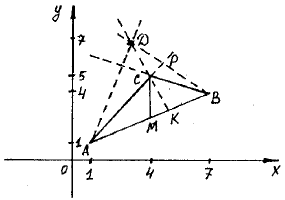
Решение:
1) Длину стороны  будем вычислять по формуле:
будем вычислять по формуле:
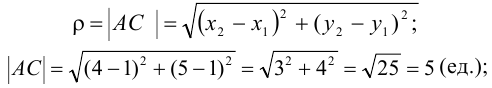
2) уравнение прямой, проходящей через две точки, имеет вид
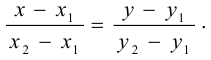
Подставив координаты точек  (1; 1) и
(1; 1) и 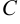 (4; 5) в уравнение, получим:
(4; 5) в уравнение, получим:
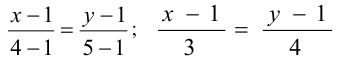
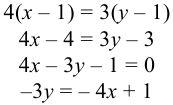
 — уравнение стороны
— уравнение стороны  ; угловой коэффициент
; угловой коэффициент  ;
;
3) так как медиана  делит сторону
делит сторону 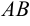 пополам, то координаты точки
пополам, то координаты точки 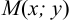 найдем по формуле:
найдем по формуле:
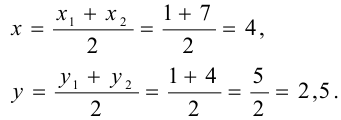
Значит, 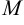 (4; 2,5).
(4; 2,5).
Уравнение медианы запишем в виде:
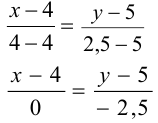
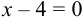 или
или
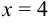 — уравнение медианы
— уравнение медианы  ;
;
4) внутренний угол 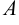 будем вычислять по формуле:
будем вычислять по формуле:
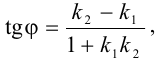
где 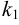 — угловой коэффициент стороны
— угловой коэффициент стороны 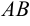 ;
; 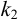 — угловой коэффициент стороны
— угловой коэффициент стороны  . Угловой коэффициент будем вычислять по формуле:
. Угловой коэффициент будем вычислять по формуле:
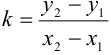 , где
, где  и
и 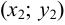 — координаты точек, через которые проходит прямая. Угловой коэффициент стороны
— координаты точек, через которые проходит прямая. Угловой коэффициент стороны 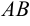 :
: 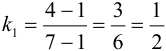 , а стороны
, а стороны  :
: 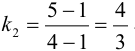 . Подставив эти данные в формулу, имеем:
. Подставив эти данные в формулу, имеем: 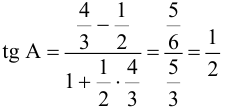 ,
,  ;
;
5) чтобы найти координаты точки пересечения всех высот треугольника, надо знать их уравнения. Так как три высоты пересекаются в одной точке, то достаточно найти уравнение двух высот, решить систему и найти координаты точки их пересечения.
Пусть 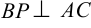 . Так как
. Так как 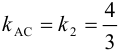 , то из условия перпендикулярности прямых имеем:
, то из условия перпендикулярности прямых имеем: 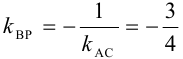 .
.
Высота  проходит через точку
проходит через точку 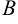 (Т; 4) и имеет угловой коэффициент
(Т; 4) и имеет угловой коэффициент 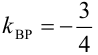 . Напишем уравнение высоты в виде уравнения пучка прямых
. Напишем уравнение высоты в виде уравнения пучка прямых 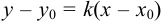 .
.
Имеем: 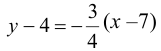
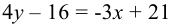
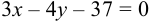 — уравнение
— уравнение  .
.
Аналогично найдем уравнение высоты 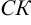 .
.
Пусть  . Так как
. Так как 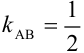 , то
, то 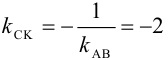 .
.
Подставляя в 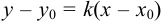 координаты точки
координаты точки 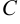 (4; 5) и
(4; 5) и 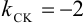 , имеем:
, имеем:
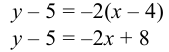
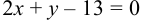 — уравнение высоты
— уравнение высоты 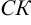 .
.
Координаты точки пересечения высот  находим, решая систему двух уравнений:
находим, решая систему двух уравнений:
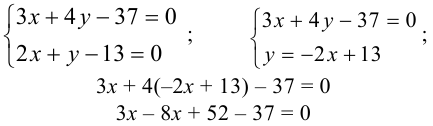
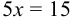 или
или 
т. е. точка  (3; 7) является точкой пересечения высот
(3; 7) является точкой пересечения высот 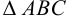 .
.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Угол между прямыми задача с решением |
| Расстояние от точки до прямой задача с решением |
| Векторы и операции над ними задачи с решением |
| Плоскость и прямая в пространстве задача с решением |

