Для связи в whatsapp +905441085890

Решение задач с помощью неравенств

Задачи, решаемые с помощью неравенств

Задача №128

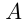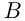Расстояние между станциями Решение задач с помощью неравенств и Решение задач с помощью неравенств равно 360 км. В одно и то же время из А и из В навстречу друг другу выезжают два поезда. Поезд из А прибывает в В не ранее, чем через 5 часов. Если бы его скорость была в 1,5 раза больше, чем на самом деле, то он встретил бы поезд из В раньше, чем через 2 часа после своего выхода из А. Скорость какого поезда больше?

Решение:

Пусть скорость поезда из 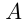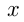Решение задач с помощью неравенств Решение задач с помощью неравенств, а скорость поезда из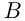 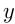Решение задач с помощью неравенств Решение задач с помощью неравенств км/ч. Запишем неравенства:

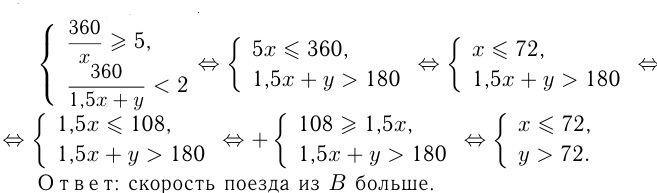
Решение задач с помощью неравенств

Задача №129

От пристани 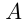Решение задач с помощью неравенств вниз по реке, скорость течения которой равна 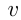Решение задач с помощью неравенств км/ч, отходит плот. Через час вслед за ним выходит катер, скорость которого в стоячей воде равна 10 км/ч. Догнав плот, катер возвращается обратно. Определить все те значения 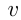Решение задач с помощью неравенств, при которых к моменту возвращения катера в 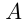Решение задач с помощью неравенств плот проходит более 15 км.

Решение:

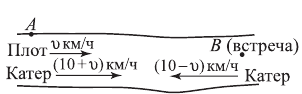
Решение задач с помощью неравенств

За 1 час плот проплыл 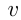Решение задач с помощью неравенств км, т. к. двигался со скоростью течения 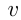Решение задач с помощью неравенств км/ч. Разница скоростей катера и плота при движении по течению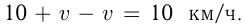 Решение задач с помощью неравенств

Время движения катера до встречи с плотом 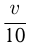Решение задач с помощью неравенств ч. После 1 часа движения плот проплыл еще 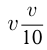Решение задач с помощью неравенств км, т.е. 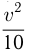Решение задач с помощью неравенств км. Таким образом, общий путь плота до встречи 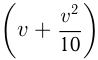Решение задач с помощью неравенств км. Этот же путь должен проделать катер при движении обратно к пристани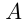 Решение задач с помощью неравенств

Время обратного движения катера равно 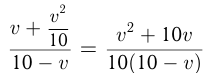Решение задач с помощью неравенствч., т.к. скорость катера против течения равна 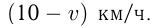Решение задач с помощью неравенств За это время плот уйдет на расстояние 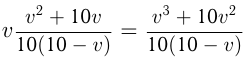Решение задач с помощью неравенств км.Общий путь плота

Решение задач с помощью неравенств

Задача №130

Три друга решили купить одну книгу. Первому не хватало для покупки книги 14 руб, второму — 37 руб., а третьему — 25 руб. Когда они сложили свои деньги вместе, то полученной суммы им также не хватило. Сколько стоит книга?

Решение:

Пусть книга стоит 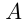Решение задач с помощью неравенств рублей; 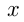Решение задач с помощью неравенств руб. было у 1-го друга, 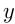Решение задач с помощью неравенств руб. — у 2-го и 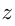Решение задач с помощью неравенств руб. у 3-го. Из условий получаем

Решение задач с помощью неравенств

Задача №131

В двух бригадах вместе более 27 человек. Число членов 1-й бригады более чем в 2 раза превышает число членов 2-й, уменьшенное на 12. Число членов 2-й бригады более чем в 9 раз превышает число членов 1-й, уменьшенное на 10. Сколько человек в каждой бригаде?

Решение:

Допустим, в 1-й бригаде 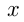Решение задач с помощью неравенств, а во 2-й — 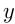Решение задач с помощью неравенств чел. Тогда

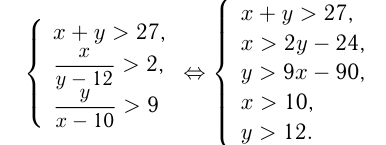
Решение задач с помощью неравенств

Известно, что можно складывать неравенства одного знака. Берем 2-е и 3-е неравенства.

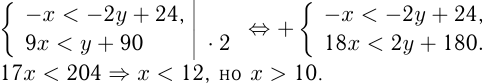
Решение задач с помощью неравенств

Т. к. 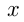Решение задач с помощью неравенств — целое число, то 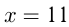Решение задач с помощью неравенств. Берем 1 -е и 2-е неравенства:

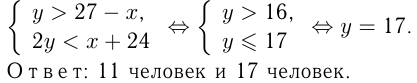
Решение задач с помощью неравенств

Задача №132

Двум бригадам общей численностью 18 человек было поручено организовать в течение 3 суток непрерывное дежурство по одному человеку. Первые двое суток дежурили члены 1-й бригады, распределив между собой это время поровну. Известно, что во 2-й бригаде 3 девушки, а остальные юноши, причем девушки дежурили по 1 часу, а все юноши распределили между собой остаток дежурства поровну. При подсчете оказалось, что общая продолжительность дежурства каждого юноши 2-й бригады и любого члена 1-й бригады меньше 9 часов. Сколько человек в каждой бригаде?

Решение:

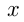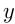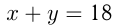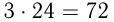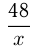Пусть в 1-й бригаде Решение задач с помощью неравенств, а во 2-й — Решение задач с помощью неравенств чел. Тогда получим Решение задач с помощью неравенств ; общее время дежурства Решение задач с помощью неравенств ч. Решение задач с помощью неравенствч — время дежурства одного человека 1-й бригады.

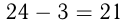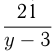Т. к. 3 девушки 2-й бригады дежурили 3 часа, то юноши 2-й бригады дежурили Решение задач с помощью неравенств ч. Решение задач с помощью неравенств ч — время дежурства одного юноши 2-й бригады.

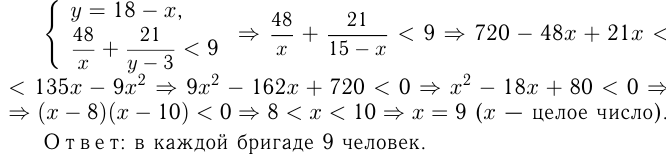
Решение задач с помощью неравенств

Задача №133

Груз вначале погрузили в вагоны вместимостью по 80 тонн, но один вагон оказался загружен неполностью. Тогда весь груз переложили в вагоны вместимостью по 60 тонн, однако понадобилось на 8 вагонов больше и при этом все равно один вагон оказался неполностью загруженным. Наконец, груз переложили в вагоны вместимостью по 50 тонн, однако понадобилось еще на 5 вагонов больше, при этом все такие вагоны были загружены полностью. Сколько тонн груза было?

Решение:

Пусть было 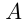Решение задач с помощью неравенств тонн груза их 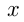Решение задач с помощью неравенств— первоначальное количество вагонов.

Из условий

Решение задач с помощью неравенств

Задача №133

В двух ящиках находится более 29 одинаковых деталей. Число деталей в 1-м ящике, уменьшенное на 2, более чем в 3 раза превышает число деталей во 2-м. Утроенное число деталей в 1-м ящике превышает удвоенное число деталей во 2-м, но менее чем на 60. Сколько деталей в каждом ящике?

Решение:

Если в 1-м ящике 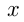Решение задач с помощью неравенств, а во 2-м 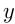Решение задач с помощью неравенств деталей, то

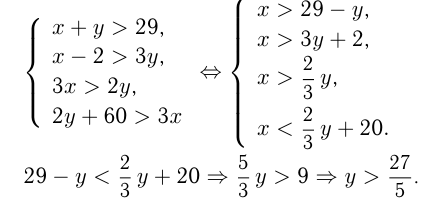
Решение задач с помощью неравенств
Решение задач с помощью неравенств

Задача №134

Группа людей построена в колонну по 8 человек в ряд, но один ряд неполный. Если эту группу перестроить по 7 человек в ряд, то все ряды будут полными, но их число увеличится на 2. Если эту группу построить по 5 человек в ряд, то рядов будет еще на 7 больше, и один ряд опять будет неполным. Сколько всего людей в группе?

Решение:

Пусть в группе 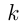Решение задач с помощью неравенств человек и первоначально было 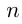Решение задач с помощью неравенств рядов. Тогда

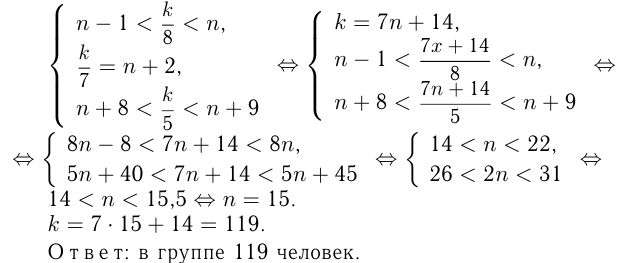
Решение задач с помощью неравенств

Этот материал взят со страницы решения задач по математике:

Решение задач по математике

Возможно вам будут полезны эти страницы:

Решение задач на числа по математике
Решение задач с целочисленными неизвестными по математике
Решение задач на прогрессии по математике
Решение задач на функции по математике