Оглавление:

Прежде чем изучать готовые решения задач по молекулярной физике, нужно знать теорию, поэтому для вас я подготовила краткую теорию по разделу «молекулярная физика», и примеры решения в которых подробно решены задачи.
Эта страница подготовлена для школьников и студентов.
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
Молекулярная физика и термодинамика. Основы молекулярно-кинетической теории. Определения, понятия и законы
Молекулярная физика — это раздел физики, изучающий строение и свойства вещества в различных агрегатных состояниях, исходя из молекулярно-кинетических представлений.
Основные положения молекулярно-кинетической теории и их опытное обоснование. Основные положения молекулярно-кинетической теории состоят в следующем:
- любое вещество состоит из молекул — наименьших устойчивых частиц данного вещества, обладающих всеми его химическими свойствами;
- все молекулы находятся в состоянии непрерывного хаотического движения, характер которого зависит от агрегатного состояния вещества;
- между молекулами действуют силы притяжения и отталкивания.
Множество прямых и косвенных доказательств реальности молекул позволяют считать молекулярно-кинетические представления о строении вещества абсолютно достоверными. Основные положения молекулярно-кинетической теории подтверждаются многочисленными опытами с использованием достижений современной экспериментальной техники. С помощью ионного проектора получают изображения кристаллов, по которым можно представить их строение. Электронные микроскопы позволили получить изображения кристаллов, по которым оказалось возможным определение расстояний между отдельными атомами и молекулами. Одним из важнейших прямых доказательств справедливости молекулярно-кинетической теории газов являются измерения значений скоростей молекул газов и сравнение этих результатов со значениями, полученными на основании теории.
Броуновское движение
Большое значение в обосновании молекулярно-кинетической теории имело в свое время открытие английского ботаника Р. Броуна. В 1827 году он обнаружил беспорядочное движение видимых в микроскоп частиц цветочной пыльцы, взвешенных в воде (названое впоследствии броуновским движением). Наблюдаемые частицы размером примерно в 1 мкм совершали неупорядоченные движения, описывая сложные зигзагообразные траектории. Многочисленные эксперименты, проведенные французским ученым Ж. Перреном, позволили установить основные закономерности броуновского движения: его интенсивность не зависит от времени, но возрастает с ростом температуры среды, уменьшением ее вязкости и размеров частиц.
Объяснить броуновское движение и его закономерности смогла лишь молекулярно-кинетическая теория. Причиной броуновского движения является тепловое движение молекул среды и отсутствие точной компенсации ударов, испытываемых частицей со стороны окружающих ее молекул. Импульс одной молекулы слишком мал, чтобы результат ее столкновения с броуновской частицей можно было увидеть под микроскопом. Но если с частицей сталкивается сразу большое число молекул, случайно движущихся в одном направлении, то они могут вызвать ее заметное смещение. Чем меньше размеры и масса частицы, тем более заметными становятся изменения ее импульса во времени.
Количественная теория броуновского движения была разработана А. Эйнштейном и М. Смолуховским в 1906 году. Она полностью объяснила все закономерности этого явления.
Масса и размер молекул
Современные приборы позволяют рассматривать отдельные атомы на поверхностях тел и измерять их размеры. Так, например, диаметр атома углерода, измеренный с помощью туннельного микроскопа, оказался равным 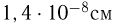 . Такой же порядок имеют размеры других атомов и большинства молекул. В частности, размер молекулы водорода составляет
. Такой же порядок имеют размеры других атомов и большинства молекул. В частности, размер молекулы водорода составляет 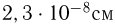 .
.
Зная размер молекулы какого-либо вещества, можно оценить ее массу. Например, диаметр молекулы воды примерно равен 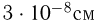 . Считая, что молекулы в воде упакованы плотно, т.е. пренебрегая межмолекулярными промежутками, легко получить для массы одной молекулы
. Считая, что молекулы в воде упакованы плотно, т.е. пренебрегая межмолекулярными промежутками, легко получить для массы одной молекулы 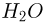 следующую оценку:
следующую оценку: 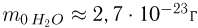 . Массы такого же порядка имеют молекулы других веществ (за исключением огромных молекул сложных органических соединений, содержащих тысячи атомов). Наиболее точно массы атомов и молекул измеряются с помощью современных масс-спектрометров.
. Массы такого же порядка имеют молекулы других веществ (за исключением огромных молекул сложных органических соединений, содержащих тысячи атомов). Наиболее точно массы атомов и молекул измеряются с помощью современных масс-спектрометров.
Так как массы молекул очень малы, удобно использовать на практике не абсолютные значения масс, а относительные. Относительной молекулярной (или атомной) массой вещества называют отношение массы молекулы (или атома) данного вещества к 1/12 массы атома углерода 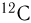 .
.
Моль вещества. Постоянная Авогадро
Количество вещества 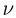 пропорционально числу структурных единиц (атомов или молекул), из которых оно состоит. Поскольку число таких единиц в макроскопических телах огромно, принято использовать в расчетах не абсолютное их число, а относительное. В системе СИ количество вещества выражают в молях.
пропорционально числу структурных единиц (атомов или молекул), из которых оно состоит. Поскольку число таких единиц в макроскопических телах огромно, принято использовать в расчетах не абсолютное их число, а относительное. В системе СИ количество вещества выражают в молях.
Один моль — это количество вещества, в котором содержится столько же структурных единиц (молекул или атомов), сколько атомов содержится в углероде 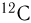 массой 12 г.
массой 12 г.
В одном моле любого вещества содержится одно и то же число структурных единиц, из которых оно состоит. Это число называют постоянной Авогадро 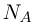 . Постоянная Авогадро равна
. Постоянная Авогадро равна 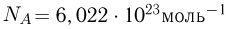 .
.
Молярной массой 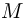 называется величина, равная отношению массы вещества
называется величина, равная отношению массы вещества 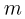 к количеству вещества
к количеству вещества 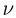 :
:
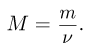
Иными словами, молярная масса — это масса вещества, взятого в количестве одного моля. Она измеряется в граммах на моль и численно равна относительной молекулярной (или атомной) массе вещества.
Характер теплового движения молекул в газах, жидкостях и твердых телах
Характер теплового движения в веществе зависит от его агрегатного состояния. Молекулы (атомы) в твердом теле совершают беспорядочные колебания относительно положений, в которых силы притяжения и отталкивания со стороны соседних молекул (атомов) уравновешены. В жидкости молекулы не только колеблются около положения равновесия, но и совершают перескоки из одного положения равновесия в соседнее. Эти перескоки являются причиной текучести жидкости, ее способности принимать форму сосуда. В газах расстояния между молекулами в среднем значительно больше размеров молекул. Силы отталкивания на больших расстояниях малы, поэтому газы легко сжимаются. Практически отсутствуют между молекулами газа и силы притяжения, поэтому газы обладают свойством неограниченно расширяться.
Тепловое равновесие
На основании многочисленных экспериментов установлено очень важное свойство тепловых явлений: тело или система тел при неизменных внешних условиях самопроизвольно переходит в состояние теплового равновесия. Тепловым, или термодинамическим равновесием называют такое состояние, при котором все макроскопические параметры системы сколь угодно долго остаются постоянными. Это означает, что не меняются объем и давление, не происходит теплообмен (передача энергии) между частями системы, отсутствуют взаимные превращения газов, жидкостей, твердых тел и т.д. Но микроскопические процессы (движение молекул, их столкновения, обмен скоростями) в системе не прекращаются и при тепловом равновесии.
Температура и ее физический смысл
Физический параметр, одинаковый во всех частях системы тел, находящихся в состоянии теплового равновесия, называется температурой. Если при контакте двух тел никакие их физические параметры не изменяются, то между телами нет теплообмена и температура тел одинакова.
Способы измерения температуры основываются на следующем утверждении, которое является обобщением многочисленных экспериментальных данных: Если тело 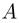 находится в тепловом равновесии с телом
находится в тепловом равновесии с телом 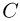 , а тело
, а тело 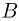 тоже находится в тепловом равновесии с телом
тоже находится в тепловом равновесии с телом 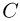 , то тела
, то тела 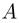 и
и 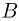 также находятся в состоянии теплового равновесия. Это дает возможность сравнивать состояния теплового равновесия тел, не приводя их в непосредственный контакт.
также находятся в состоянии теплового равновесия. Это дает возможность сравнивать состояния теплового равновесия тел, не приводя их в непосредственный контакт.
Шкала температур Цельсия
Для измерения температуры можно воспользоваться зависимостями любой макроскопической величины от температуры, а именно, объема, давления, электрического сопротивления и т.д. На практике чаще всего используют зависимость объема жидкости (ртути или спирта) от температуры. По шкале Цельсия за начало отсчета (0) принимают температуру тающего льда; второй постоянной точкой (100) считают температуру кипения воды при нормальном атмосферном давлении. Шкалу между точками 0 и 100 делят на 100 равных частей, называемых градусами (1 °C). Перемещение столбика жидкости на одно деление соответствует изменению температуры на 1 °C.
Идеальный газ
Для объяснения свойств вещества в газообразном состоянии используется модель идеального газа. В этой модели предполагается, что молекулы обладают пренебрежимо малым объемом по сравнению с объемом сосуда, между молекулами не действуют силы притяжения, при соударениях молекул друг с другом и со стенками сосуда действуют силы упругого отталкивания.
Основное уравнение молекулярно-кинетической теории идеального газ
Одним из самых важных успехов молекулярно-кинетической теории явилось количественное объяснение давления газа на стенки сосуда. Основное уравнение молекулярно-кинетической теории идеального газа было выведено в предположении, что молекулы газа при столкновениях со стенками сосуда взаимодействуют с ними по законам механики как упругие тела. Согласно этому уравнению,
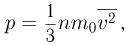
где 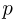 — давление газа,
— давление газа, 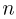 — концентрация молекул (число молекул в единице объема),
— концентрация молекул (число молекул в единице объема), 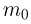 — масса молекулы
— масса молекулы 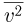 — среднее значение квадрата скорости молекул. Обозначив через
— среднее значение квадрата скорости молекул. Обозначив через 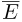 среднюю кинетическую энергию поступательного движения молекул газа
среднюю кинетическую энергию поступательного движения молекул газа
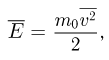
уравнение (2.1.2) можно записать в эквивалентной форме
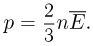
Средняя кинетическая энергия молекул и температура
Основное уравнение молекулярно-кинетической теории идеального газа устанавливает связь макроскопического параметра — давления — с микроскопическими параметрами газа — средней кинетической энергией и концентрацией молекул. Но, измерив только давление газа, мы не можем в отдельности узнать ни среднее значение кинетической энергии молекул, ни их концентрацию. Для нахождения микроскопических параметров газа нужны измерения еще одной физической величины, как-то связанной со средней кинетической энергией молекул. Такой величиной является температура.
Для установления этой связи используется известный из экспериментов факт, что для большинства разреженных газов, находящихся в состоянии теплового равновесия, отношение произведения давления газа на его объем к числу молекул является одинаковым:
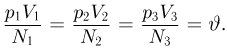
Этот опытный факт позволяет принять величину 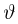 в качестве естественной меры температуры. Так как
в качестве естественной меры температуры. Так как 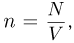 то с учетом (2.1.4) получим
то с учетом (2.1.4) получим
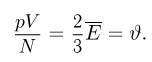
Следовательно, средняя кинетическая энергия молекул любых газов, находящихся в тепловом равновесии, одинакова. Величина 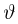 равна двум третям средней кинетической энергии теплового движения молекул газа и выражается в джоулях. В физике температуру выражают в градусах, принимая, что температура
равна двум третям средней кинетической энергии теплового движения молекул газа и выражается в джоулях. В физике температуру выражают в градусах, принимая, что температура 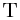 и величина
и величина 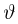 связаны уравнением
связаны уравнением
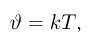
где 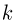 — коэффициент пропорциональности, зависящий от выбора единицы температуры. Окончательно получаем
— коэффициент пропорциональности, зависящий от выбора единицы температуры. Окончательно получаем
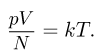
Абсолютная температурная шкала. Постоянная Больцмана
Последнее уравнение показывает, что имеется возможность выбрать температурную шкалу, не зависящую от природы газа, используемого в качестве рабочего тела. Такая шкала называется абсолютной температурной шкалой, или шкалой Кельвина. Единица температуры по абсолютной шкале, называемая кельвином (К), выбрана равной одному градусу по шкале Цельсия: 1 К = 1 °C.
При таком выборе единицы температуры коэффициент 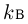 уравнении (2.1.8) принимает значение
уравнении (2.1.8) принимает значение 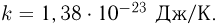 Он называется постоянной Больцмана. Постоянную Больцмана можно рассматривать как величину, связывающую температуру, выражаемую в энергетических единицах, с температурой, выраженной в градусах.
Он называется постоянной Больцмана. Постоянную Больцмана можно рассматривать как величину, связывающую температуру, выражаемую в энергетических единицах, с температурой, выраженной в градусах.
Абсолютная температура 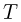 связана с температурой
связана с температурой 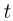 по шкале Цельсия соотношением
по шкале Цельсия соотношением
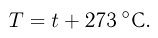
Из уравнений (2.1.6) и (2.1.8) следует, что
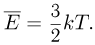
Средняя кинетическая энергия хаотического движения молекул газа пропорциональна абсолютной температуре. Из уравнений (2.1.4) и (2.1.10) можно получить, что
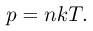
При одинаковых значениях температуры и концентрации молекул давление любых газов одинаково. Отсюда следует закон Авогадро: в равных объемах газов при одинаковых температурах и давлениях содержится одинаковое число молекул.
Используя уравнения (2.1.3) и (2.1.10), найдем средний квадрат скорости поступательного движения молекул:
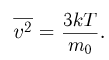
Квадратный корень из этой величины называется средней квадратичной скоростью:
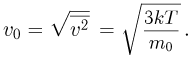
Уравнение Клапейрона-Менделеева (уравнение состояния идеального газа). Универсальная газовая постоянная
Каждая физически однородная система, состоящая из большого числа частиц (газ, жидкость или твердое тело) и находящаяся в состоянии теплового равновесия, характеризуется своим уравнением состояния, т.е. уравнением, связывающим давление, объем и абсолютную температуру: 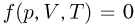 . Наиболее просто выглядит уравнение состояния идеального газа, хорошо известны различные приближенные уравнения, описывающие состояние реальных газов. В то же время, для жидкостей из-за их сложного строения до сих пор не удалось получить общего уравнения состояния. Нет универсального уравнения состояния и для твердых тел.
. Наиболее просто выглядит уравнение состояния идеального газа, хорошо известны различные приближенные уравнения, описывающие состояние реальных газов. В то же время, для жидкостей из-за их сложного строения до сих пор не удалось получить общего уравнения состояния. Нет универсального уравнения состояния и для твердых тел.
Уравнение, устанавливающее связь между давлением, объемом и температурой газов, было получено французским физиком Б. Клапейроном путем обобщения многочисленных экспериментальных данных. В наиболее удобной форме, используемой вплоть до настоящего времени, его впервые применил Д.И. Менделеев. Поэтому уравнение состояния идеального газа называется также уравнением Клапейрона-Менделеева. Оно имеет вид
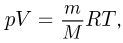
где 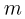 — масса газа,
— масса газа, 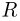 — универсальная газовая постоянная, равная произведению постоянной Авогадро
— универсальная газовая постоянная, равная произведению постоянной Авогадро 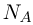 на постоянную Больцмана
на постоянную Больцмана 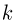 :
: 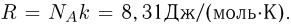 Используя выражение для плотности газа
Используя выражение для плотности газа 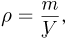 уравнение Клапейрона-Менделеева можно записать эквивалентной форме, более удобной в некоторых случаях:
уравнение Клапейрона-Менделеева можно записать эквивалентной форме, более удобной в некоторых случаях:
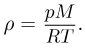
Изотермический, изохорный и изобарный процессы
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трех параметров — давление, объем или температура — остаются неизменными. Особую роль в физике и технике играют три процесса — изотермический, изохорный и изобарный.
Изотермическим процессом называется процесс, протекающий при постоянной температуре 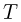 . Из уравнения состояния идеального газа следует, что в таком процессе произведение давления газа на его объем должно оставаться постоянным:
. Из уравнения состояния идеального газа следует, что в таком процессе произведение давления газа на его объем должно оставаться постоянным:
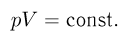
График изотермического процесса называется изотермой. На плоскости переменных объем — давление он представляет собой гиперболу.
Уравнение (2.1.16) было получено экспериментально английским физиком Р. Бойлем и французским физиком Э. Мариоттом задолго до создания молекулярно-кинетической теории. Это уравнение называют законом Бойля-Мариотта.
Процесс, протекающий при постоянном объеме, называется изохорным. Из уравнения (2.1.14) вытекает, что при 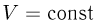
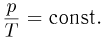
График изохорного процесса называется изохорой. На плоскости переменных температура — давление он представляет собой отрезок прямой, продолжение которого проходит через начало координат. Экспериментальным путем зависимость давления газа от температуры исследовал французский физик Ж. Шарль. Поэтому уравнение (2.1.17) называется законом Шарля.
Процесс изменения состояния газа при постоянном давлении называется изобарным. Его уравнение имеет вид
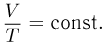
Этот закон был установлен экспериментально французским ученым Ж. Гей-Люссаком и носит название закона Гей-Люссака. График изобарного процесса называется изобарой. На плоскости переменных температура — объем он представляет собой отрезок прямой, продолжение которого проходит через начало координат.
Указания по решению задач
Решение задач по этой теме следует начинать с анализа тех состояний теплового равновесия, в которых по условию находится газ. Для каждого из таких состояний нужно записать все параметры газа: давление, объем, температуру и его массу, а также установить связь между ними.
Часто в задачах оказывается полезным использование закона парциальных давлений (закона Дальтона). Напомним, что парциальным называется давление, которое оказывал бы газ, входящий в состав газовой смеси, если бы он один занимал весь объем. Согласно закону Дальтона, давление смеси химически не взаимодействующих газов равно сумме их парциальных давлений. С точки зрения молекулярно-кинетической теории закон Дальтона означает, что действия на стенки сосуда молекул каждого из газов складываются. В частности, закон Дальтона применим и при добавлении в сосуд, в котором уже находится газ под давлением р, некоторого количества этого же газа. В этом случае парциальное давление добавленного газа можно рассчитывать так, как если бы сосуд был пустой. Результирующее давление складывается из этого парциального давления и давления р, которое было в сосуде первоначально.
Часто в задачах отдельные порции газа изолируются друг от друга подвижными поршнями. В этом случае давления газа по разные стороны поршня не независимы, а связаны между собой условием механического равновесия поршня. В частности, если неподвижный сосуд располагается вертикально, разность сил давления газа снизу и сверху от поршня равна его весу.
Примеры решения задач №1:
Задача №2.1.1.
Атмосферное давление на пике Ленина (высота 7134 м) 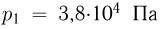 . Определить плотность воздуха
. Определить плотность воздуха 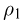 на вершине при температуре
на вершине при температуре 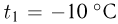 , если при нормальных условиях
, если при нормальных условиях 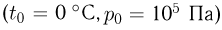 , плотность воздуха
, плотность воздуха 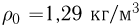 .
.
Решение:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева) можно записать в следующей форме: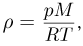
где 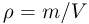 — плотность газа,
— плотность газа, 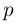 — давление,
— давление, 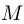 — молярная масса,
— молярная масса, 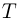 — абсолютная температура газа. Учитывая, что
— абсолютная температура газа. Учитывая, что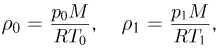
где 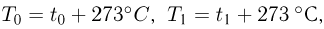 получаем ответ:
получаем ответ:
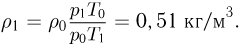
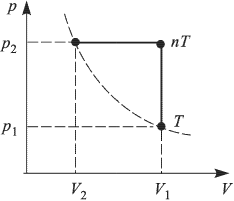
Задача №2.1.2.
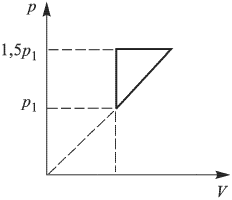
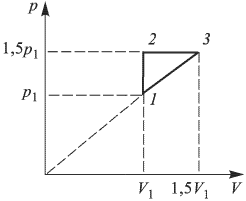
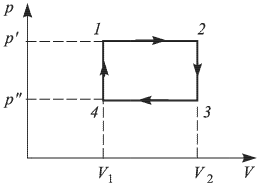
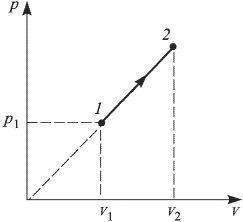
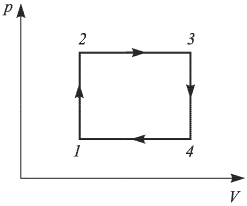
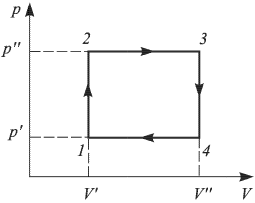
Найти отношение 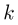 максимальной плотности идеального газа к его минимальной плотности, которые достигаются при циклическом процессе, показанном на рисунке.
максимальной плотности идеального газа к его минимальной плотности, которые достигаются при циклическом процессе, показанном на рисунке.
Решение:
Значения плотности газа в точках 1, 2 и 3 (см. рисунок) равны:
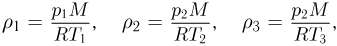
где 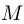 — молярная масса газа,
— молярная масса газа, 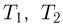 и
и
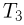 — температуры газа в этих точках. Поскольку объем газа в точках 1 и 2 один и тот же,
— температуры газа в этих точках. Поскольку объем газа в точках 1 и 2 один и тот же, 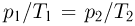 . Следовательно,
. Следовательно, 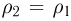 т.е. на участке 1 — 2 плотность газа не меняется. На участке 2 — 3, проходящем при постоянном давлении,
т.е. на участке 1 — 2 плотность газа не меняется. На участке 2 — 3, проходящем при постоянном давлении, 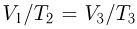 , откуда следует, что
, откуда следует, что 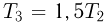 . Поэтому
. Поэтому 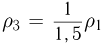 . Таким образом, максимальная плотность газа достигается в точках 1 и 2, а минимальная — в точке 3. Ответ:
. Таким образом, максимальная плотность газа достигается в точках 1 и 2, а минимальная — в точке 3. Ответ: 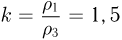 .
.
Задача №2.1.3.
С идеальным одноатомным газом проводят процесс 1 — 2, показанный на рисунке. Во сколько раз 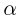 при этом изменится средняя кинетическая энергия молекулы газа?
при этом изменится средняя кинетическая энергия молекулы газа?
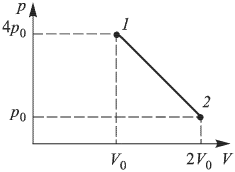
Решение:
Поскольку средняя кинетическая энергия молекулы одноатомного газа
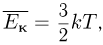
искомое отношение энергий равно отношению абсолютных температур газа в состояниях 2 и 1, т.е. 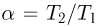 . Записывая уравнение Клапейрона-Менделеева для этих состояний, имеем:
. Записывая уравнение Клапейрона-Менделеева для этих состояний, имеем:
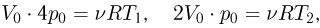
где 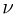 — количество молей газа,
— количество молей газа, 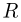 — универсальная газовая постоянная. Отсюда видно, что
— универсальная газовая постоянная. Отсюда видно, что 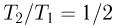 . Следовательно,
. Следовательно, 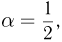 т.е. средняя кинетическая энергия молекулы газа в процессе 1 — 2 уменьшится в 2 раза.
т.е. средняя кинетическая энергия молекулы газа в процессе 1 — 2 уменьшится в 2 раза.
Задача №2.1.4.
Горизонтальный цилиндр с газом разделен на три камеры двумя неподвижными поршнями. Температура газа во всех камерах одинакова и равна 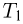 . Давление газа в первой камере
. Давление газа в первой камере 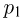 , объем
, объем 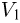 , во второй
, во второй 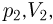 в третьей соответственно
в третьей соответственно 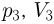 . Каково будет давление
. Каково будет давление 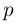 в камерах после того как, освободив поршни, дать им возможность свободно двигаться, а температуру газа сделать равной
в камерах после того как, освободив поршни, дать им возможность свободно двигаться, а температуру газа сделать равной 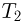 ?
?
Решение:
Запишем уравнения состояния для порций газа в камерах:
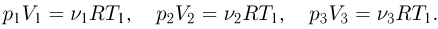
Отсюда найдем количества газа в каждой камере:
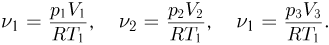
Когда поршни освободят, давление во всех камерах станет одинаковым и уравнение состояния газа примет вид:
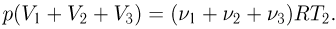
Подставляя сюда выше найденные количества газа, получаем ответ:
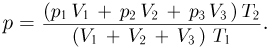
Задача №2.1.5.
Баллон, содержащий 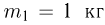 азота, при испытании на прочность взорвался при температуре
азота, при испытании на прочность взорвался при температуре 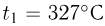 . Какую массу водорода
. Какую массу водорода 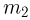 можно было бы хранить в таком баллоне при температуре
можно было бы хранить в таком баллоне при температуре 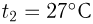 , имея пятикратный запас прочности? Молярная масса азота
, имея пятикратный запас прочности? Молярная масса азота 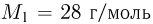 , водорода
, водорода 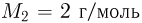 .
.
Решение:
Из уравнения состояния азота следует, что давление, при, котором взорвался баллон, 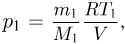 где
где 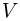 — объем баллона. По условию водород можно хранить при давлении
— объем баллона. По условию водород можно хранить при давлении 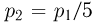 . Учитывая, что
. Учитывая, что 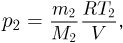 получаем ответ:
получаем ответ: 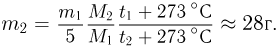
Задача №2.1.6.
В цилиндре с площадью основания 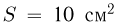 могут без трения скользить два поршня. Между поршнями находится идеальный газ, а справа и слева от них — вакуум. Поршни соединены со стенками сосуда пружинами жесткости
могут без трения скользить два поршня. Между поршнями находится идеальный газ, а справа и слева от них — вакуум. Поршни соединены со стенками сосуда пружинами жесткости 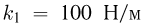 и
и 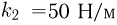 , как показано на рисунке. При температуре
, как показано на рисунке. При температуре 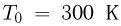 давление газа
давление газа 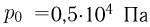 и расстояние между поршнями
и расстояние между поршнями 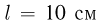 . Найти температуру газа
. Найти температуру газа 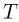 , при которой расстояние между поршнями увеличится до
, при которой расстояние между поршнями увеличится до 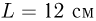 .
.

Решение:
Уравнения начального и конечного состояния газа имеют вид:
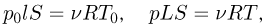
откуда 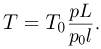
Из условия равновесия поршней имеем:
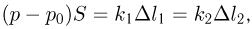
где 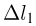 и
и 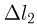 — смещения левого и правого поршней соответственно, причем
— смещения левого и правого поршней соответственно, причем 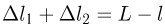 . Отсюда
. Отсюда 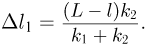 Объединяя записанные выражения, получаем ответ:
Объединяя записанные выражения, получаем ответ:
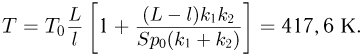
Задача №2.1.7.
Закрытый с обоих концов горизонтальный цилиндр заполнен идеальным газом при температуре 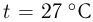 и разделен подвижным теплонепроницаемым поршнем на две равные части длиной
и разделен подвижным теплонепроницаемым поршнем на две равные части длиной 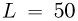 см каждая. На какую величину
см каждая. На какую величину 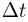 нужно повысить температуру газа в одной половине цилиндра, чтобы поршень сместился на расстояние
нужно повысить температуру газа в одной половине цилиндра, чтобы поршень сместился на расстояние 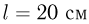 при неизменной температуре газа во второй половине цилиндра?
при неизменной температуре газа во второй половине цилиндра?
Решение:
Для части газа, имеющей постоянную температуру, справедлив закон Бойля-Мариотта, согласно которому
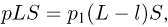
где 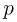 — первоначальное давление газа в цилиндре,
— первоначальное давление газа в цилиндре, 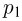 — давление в цилиндре после нагревания половины газа,
— давление в цилиндре после нагревания половины газа, 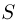 — площадь поршня. Уравнение состояния, записанное для газа в другой части цилиндра, дает нам соотношение
— площадь поршня. Уравнение состояния, записанное для газа в другой части цилиндра, дает нам соотношение
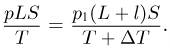
Исключая из этих равенств 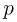 и
и 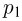 , получаем ответ:
, получаем ответ: 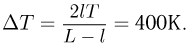
Задача №2.1.8.
Сосуд, содержащий идеальный газ при температуре 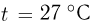 , снабжен клапаном, открывающимся при перепаде давлений
, снабжен клапаном, открывающимся при перепаде давлений 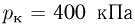 . Газ нагревают до температуры
. Газ нагревают до температуры 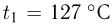 , при этом часть газа выходит из сосуда через клапан. Найти давление
, при этом часть газа выходит из сосуда через клапан. Найти давление 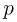 , которое установится в сосуде после охлаждения газа до начальной температуры
, которое установится в сосуде после охлаждения газа до начальной температуры 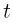 . Атмосферное давление
. Атмосферное давление 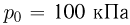 .
.
Решение:
При нагревании газа в сосуде его давление будет повышаться до величины 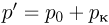 , после чего давление будет оставаться постоянным и равным
, после чего давление будет оставаться постоянным и равным 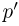 , а излишек газа будет выходить наружу. Из уравнения состояния газа в конце нагрева
, а излишек газа будет выходить наружу. Из уравнения состояния газа в конце нагрева
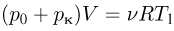
можно найти количество газа, оставшегося в сосуде:
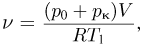
где 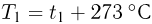 . Записывая уравнение состояния этого количества газа при температуре
. Записывая уравнение состояния этого количества газа при температуре 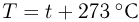 :
:
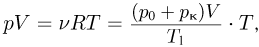
получаем ответ: 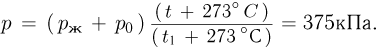
Задача №2.1.9.
Вертикально расположенный цилиндрический сосуд, закрытый подвижным поршнем массой 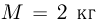 , содержит идеальный газ при температуре
, содержит идеальный газ при температуре 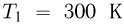 . На поршень помешают тело массой
. На поршень помешают тело массой 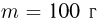 и нагревают газ так, чтобы поршень занял первоначальное положение. Найти температуру
и нагревают газ так, чтобы поршень занял первоначальное положение. Найти температуру 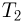 нагретого газа. Атмосферное давление не учитывать.
нагретого газа. Атмосферное давление не учитывать.
Решение:
Обозначив через 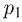 и
и 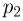 давления газа в начальном и конечном состояниях, имеем:
давления газа в начальном и конечном состояниях, имеем:
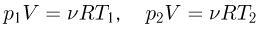
где 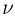 — количество газа,
— количество газа, 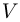 — его объем. Отсюда
— его объем. Отсюда 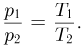 Учитывая, что
Учитывая, что 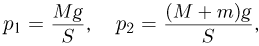
после несложных преобразований получаем ответ:
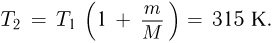
Задача №2.1.10.
В цилиндре под невесомым поршнем площадью 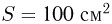 находится 1 моль идеального газа при температуре
находится 1 моль идеального газа при температуре 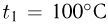 . К поршню через два блока на невесомой нерастяжимой нити подвешен груз массой
. К поршню через два блока на невесомой нерастяжимой нити подвешен груз массой 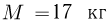 . На какую высоту
. На какую высоту 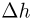 поднимется груз, если медленно охладить газ до температуры
поднимется груз, если медленно охладить газ до температуры 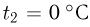 ? Атмосферное давление
? Атмосферное давление 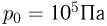 . Универсальная газовая постоянная
. Универсальная газовая постоянная 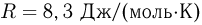 , ускорение свободного падения принять
, ускорение свободного падения принять 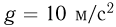 . Трением пренебречь.
. Трением пренебречь.
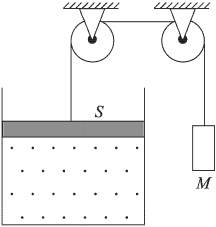
Решение:
Поршень находится под действием трех сил: силы натяжения нити 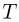 и силы давления газа в сосуде
и силы давления газа в сосуде 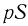 , направленных вверх, а также силы атмосферного давления
, направленных вверх, а также силы атмосферного давления 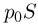 , направленной вниз. Поскольку процесс охлаждения газа является медленным, можно считать, что ускорение системы равно нулю и сила натяжения нити в каждый момент времени равна весу неподвижного груза, т.е.
, направленной вниз. Поскольку процесс охлаждения газа является медленным, можно считать, что ускорение системы равно нулю и сила натяжения нити в каждый момент времени равна весу неподвижного груза, т.е. 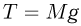 .
.
Следовательно, поршень находится в равновесии при выполнении условия:
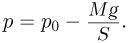
Как видно из этой формулы, давление газа 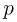 при изменении его объема постоянно. Записывая уравнение Клапейрона-Менделеева для начального и конечного состояний газа, получаем:
при изменении его объема постоянно. Записывая уравнение Клапейрона-Менделеева для начального и конечного состояний газа, получаем:
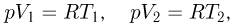
где 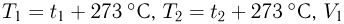 и
и 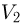 — начальный и конечный объемы газа, причем
— начальный и конечный объемы газа, причем 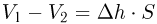 . Объединяя записанные соотношения, получаем ответ:
. Объединяя записанные соотношения, получаем ответ: 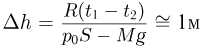 .
.
Задача №2.1.11.
В вертикально расположенном цилиндре находится кислород массой 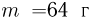 , отделенный от атмосферы поршнем, который соединен с дном цилиндра пружиной жесткостью
, отделенный от атмосферы поршнем, который соединен с дном цилиндра пружиной жесткостью 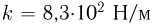 . При температуре
. При температуре 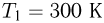 поршень располагается на расстоянии
поршень располагается на расстоянии 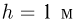 от дна цилиндра. До какой температуры
от дна цилиндра. До какой температуры 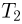 надо нагреть кислород, чтобы поршень расположился на высоте
надо нагреть кислород, чтобы поршень расположился на высоте 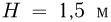 от дна цилиндра? Универсальная газовая постоянная
от дна цилиндра? Универсальная газовая постоянная 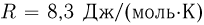 , молярная масса кислорода
, молярная масса кислорода 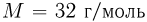 .
.
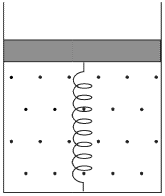
Решение:
Поскольку в условии задачи не сказано, что поршень невесом, будем полагать, что он обладает некоторой неизвестной массой, которую обозначим через 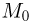 . Ничего не говорится также про атмосферное давление, поэтому будем считать, что оно действует и обозначим его через
. Ничего не говорится также про атмосферное давление, поэтому будем считать, что оно действует и обозначим его через 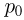 . Таким образом, на поршень действуют в общем случае четыре силы: сила тяжести
. Таким образом, на поршень действуют в общем случае четыре силы: сила тяжести 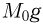 , сила упругости пружины
, сила упругости пружины 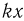 (
(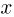 — удлинение пружины) и сила атмосферного давления
— удлинение пружины) и сила атмосферного давления 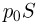 , направленные вниз, и сила давления газа в цилиндре
, направленные вниз, и сила давления газа в цилиндре 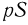 , направленная вверх. Условия равновесия поршня в начальном и конечном состояниях имеют вид:
, направленная вверх. Условия равновесия поршня в начальном и конечном состояниях имеют вид: 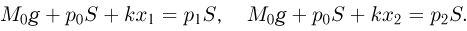
Здесь 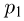 и
и 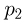 — давления газа в начальном и конечном состояниях. Вычитая из второго уравнения первое, получаем:
— давления газа в начальном и конечном состояниях. Вычитая из второго уравнения первое, получаем:
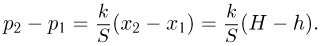
С другой стороны, из уравнения Клапейрона-Менделеева, записанного для начального и конечного состояний газа:
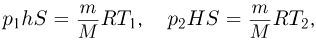 вытекает, что
вытекает, что
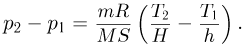
Приравнивая разности давлений газа, найденные этими двумя способами, после несложных преобразований получаем ответ:
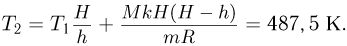
Видно, что наличие атмосферного давления и конечная масса поршня не влияют на ответ.
Задача №2.1.12.
Вертикальная цилиндрическая трубка с запаянными концами разделена на две части тонким горизонтальным поршнем, способным перемещаться вдоль нее без трения. Верхняя часть трубки заполнена неоном, а нижняя — гелием, причем массы газов одинаковы. При некоторой температуре поршень находится точно посередине трубки. После того, как трубку нагрели, поршень переместился вверх и стал делить объем трубки в отношении 1 : 3. Определить, во сколько раз 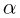 возросла абсолютная температура газов. Молярная масса неона
возросла абсолютная температура газов. Молярная масса неона 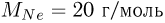 , молярная масса гелия
, молярная масса гелия 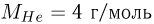 .
.
Решение:
Обозначим через 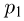 и
и 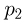 давления газов, находящихся в верхней и нижней частях трубки, соответственно. Поскольку количества газов в верхней и нижней частях трубки по условию задачи различны, а при одной и той же начальной температуре
давления газов, находящихся в верхней и нижней частях трубки, соответственно. Поскольку количества газов в верхней и нижней частях трубки по условию задачи различны, а при одной и той же начальной температуре 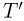 объемы этих частей одинаковы, равновесие поршня возможно только при условии, что он имеет некоторую конечную массу. Обозначив массу поршня через
объемы этих частей одинаковы, равновесие поршня возможно только при условии, что он имеет некоторую конечную массу. Обозначив массу поршня через 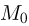 , а его площадь через
, а его площадь через 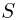 , запишем условие равновесия поршня в виде:
, запишем условие равновесия поршня в виде:
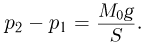
Используя уравнение Клапейрона-Менделееева для описания состояния гелия и неона при произвольной температуре 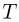 , получаем для разности их давлений следующее выражение:
, получаем для разности их давлений следующее выражение:
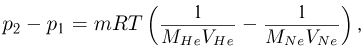
где 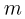 — масса каждого из газов,
— масса каждого из газов, 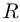 — универсальная газовая постоянная. Обозначим через
— универсальная газовая постоянная. Обозначим через 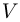 объем всей трубки. Тогда начальные объемы газов (при температуре
объем всей трубки. Тогда начальные объемы газов (при температуре 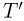 ):
): 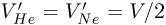 , а их конечные объемы (при температуре
, а их конечные объемы (при температуре 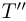 ):
): 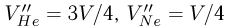 . Объединяя записанные равенства, приходим к соотношению:
. Объединяя записанные равенства, приходим к соотношению:
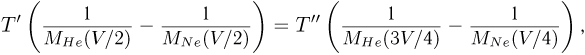 из которого после несложных преобразований получаем ответ:
из которого после несложных преобразований получаем ответ:
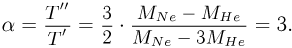
Задача №2.1.13.
Идеальный газ переводится из состояния 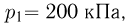 ,
, 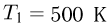 в состояние
в состояние 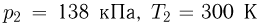 так, что объем газа меняется по закону
так, что объем газа меняется по закону 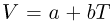 , где
, где 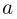 и
и 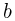 — постоянные,
— постоянные, 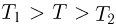 . Определить максимальную концентрацию
. Определить максимальную концентрацию 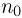 молекул газа в этом процессе. Постоянная Больцмана
молекул газа в этом процессе. Постоянная Больцмана 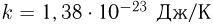 .
.
Решение:
Из уравнений начального и конечного состояний газа
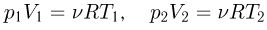
следует, что 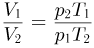 .
.
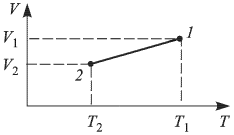
Подстановка численных значений дает: 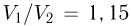 . Следовательно, зависимость
. Следовательно, зависимость  от
от 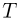 имеет вид, изображенный на рисунке, и минимальный объем в этом процессе, равный
имеет вид, изображенный на рисунке, и минимальный объем в этом процессе, равный 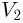 , достигается в состоянии 2. Записывая уравнение этого состояния в форме
, достигается в состоянии 2. Записывая уравнение этого состояния в форме 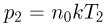 , получаем ответ:
, получаем ответ:
Элементы термодинамики. Определения, понятия и законы
Термодинамика — это наука о наиболее общих тепловых свойствах макроскопических тел. Термодинамический подход не требует каких-либо конкретных предположений о строении вещества, поэтому выводы термодинамики имеют универсальный характер. Законы термодинамики справедливы для всех тел независимо от их внутреннего строения.
Термодинамическая система — это совокупность макроскопических тел, которые могут взаимодействовать между собой и другими телами (внешней средой). Термодинамическая система состоит из настолько большого числа структурных частиц (атомов и молекул), чтобы ее состояние можно было характеризовать макроскопическими параметрами: плотностью, давлением, концентрацией веществ, образующих систему, и т.д.
Термодинамическая система находится в равновесии, если ее параметры не меняются во времени и в системе нет потоков энергии и вещества. Для равновесных термодинамических систем вводится понятие температуры как параметра состояния, имеющего одинаковое значение для всех макроскопических частей системы.
Термодинамические системы, не обменивающиеся с другими системами ни энергией, ни веществом, называются изолированными. Если система не изолирована, то ее состояние может меняться; изменение состояния системы называется термодинамическим процессом.
Внутренняя энергия системы
Все макроскопические тела наряду с механической энергией обладают также энергией, зависящей от внутреннего состояния тел. Эту энергию называют внутренней. С точки зрения молекулярно-кинетической теории внутренняя энергия макроскопического тела равна сумме кинетических энергий хаотического движения всех молекул (или атомов) и потенциальных энергий взаимодействия молекул друг с другом (но не с молекулами других тел.
Внутренняя энергия идеального газа равна кинетической энергии
хаотического движения молекул, поскольку потенциальная энергия взаимодействия молекул равна нулю. Наиболее просто рассчитывается внутренняя энергия одноатомных газов, состоящих из отдельных атомов, а не молекул. Одноатомными являются инертные газы: гелий, неон, аргон и др. С точки зрения механики одноатомный газ представляет собой систему частиц, которые совершают только поступательное движение. Молекулы двух- (и более) атомных газов могут совершать и другие виды движения — вращательное и колебательное, с которыми
тоже связана определенная энергия.
Поскольку средняя кинетическая энергия молекулы одноатомного газа равна 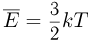 внутренняя энергия одного моля такого газа
внутренняя энергия одного моля такого газа
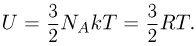
Для и 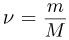 молей одноатомного идеального газа внутренняя энергия
молей одноатомного идеального газа внутренняя энергия
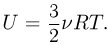
Внутренняя энергия данной массы идеального газа зависит только от температуры и не зависит ни от давления, ни от объема газа, (для неидеальных газов, а также других веществ, это, вообще говоря, неверно).
Количество теплоты и работа как меры изменения внутренней энергии. Расчет работы газа с помощью pV — диаграмм
Понятия об энергии и мере ее изменения — работе, введенные в механике, получают в термодинамике дальнейшее развитие.
Необходимым условием совершения телом (или системой тел) работы является перемещение тела под действием сил. О работе можно говорить только тогда, когда происходит изменение механического состояния тела (или системы), причем речь идет о перемещении макроскопических частей системы друг относительно друга.
Различаются работа 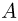 , которая совершается системой над внешними телами, и работа
, которая совершается системой над внешними телами, и работа 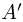 , которая совершается внешними телами над системой. Работа
, которая совершается внешними телами над системой. Работа 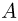 принимается положительной, работа
принимается положительной, работа 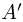 — отрицательной, причем
— отрицательной, причем 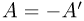 .
.
Рассмотрим работу расширения газа, т.е. работу, которую газ совершает против внешнего давления, создаваемого поршнем. Элементарная работа 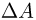 определяется формулой
определяется формулой
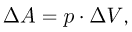
где 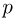 — внешнее давление,
— внешнее давление, 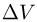 — приращение объема газа. Такой же формулой выражается элементарная работа, совершаемая не только газом, но и любым телом против внешнего давления.
— приращение объема газа. Такой же формулой выражается элементарная работа, совершаемая не только газом, но и любым телом против внешнего давления.
При расширении газ совершает положительную работу против внешних сил 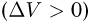 . При сжатии газа совершается отрицательная работа
. При сжатии газа совершается отрицательная работа 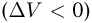 . Она совершается теми внешними телами, которые создали внешнее давление.
. Она совершается теми внешними телами, которые создали внешнее давление.
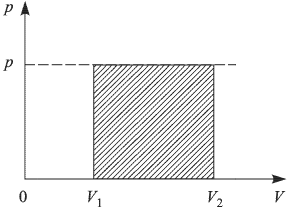
Работа расширения при изменении объема газа от 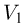 до
до 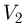 равна сумме элементарных работ. Например, в случае изобарного процесса, при котором
равна сумме элементарных работ. Например, в случае изобарного процесса, при котором 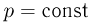 , работа расширения
, работа расширения
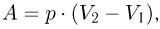
где 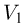 и
и 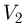 — начальный и конечный объемы газа. При изобарном расширении работа изображается на
— начальный и конечный объемы газа. При изобарном расширении работа изображается на 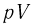 — диаграмме площадью прямоугольника (рис. 2.2.1).
— диаграмме площадью прямоугольника (рис. 2.2.1).
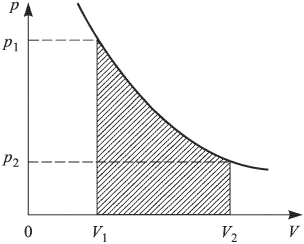
Работа расширения при любом процессе измеряется площадью на 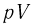 — диаграмме, ограниченной кривой процесса, осью абсцисс и вертикальными прямыми
— диаграмме, ограниченной кривой процесса, осью абсцисс и вертикальными прямыми 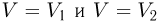 (рис. 2.2.2.).
(рис. 2.2.2.).
Работа, совершенная системой в том или ином процессе, является мерой изменения ее энергии в этом процессе. Если над телом совершается работа, то это может привести к увеличению любого вида энергии данного тела, как внутренней, так и энергии упорядоченного (поступательного) движения.
Существует также другая форма передачи энергии, при которой осуществляется непосредственный обмен энергией между хаотически движущимися частицами взаимодействующих тел. Процесс передачи энергии без совершения работы называется теплообменом. Мерой энергии, переданной в форме теплоты в процессе теплообмена, служит величина, называемая количеством теплоты.
Теплота, как и работа, является не видом энергии, а формой ее передачи. Теплота и работа обладают тем общим свойством, что они определены лишь в процессе передачи, и их численные значения зависят от вида этого процесса.
Теплоемкостью тела называется физическая величина, равная количеству теплоты 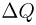 , которое необходимо сообщить телу для нагревания его на один градус:
, которое необходимо сообщить телу для нагревания его на один градус:
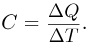
Теплоемкость тела зависит от его массы, химического состава, термодинамического состояния и вида того процесса, в котором телу передается энергия в форме теплоты.
Удельной теплоемкостью с называется теплоемкость единицы массы однородного вещества:
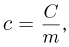
где 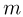 — масса вещества. Молярной теплоемкостью
— масса вещества. Молярной теплоемкостью 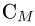 называется теплоемкость одного моля вещества:
называется теплоемкость одного моля вещества:
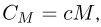
где 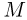 — молярная масса вещества. Удельная и молярная теплоемкости не являются постоянными величинами и в таблицах теплоемкостей указываются условия, при которых данные таблиц справедливы.
— молярная масса вещества. Удельная и молярная теплоемкости не являются постоянными величинами и в таблицах теплоемкостей указываются условия, при которых данные таблиц справедливы.
Понятие об адиабатическом процессе
Адиабатическим процессом называется термодинамический процесс, который осуществляется в системе без теплообмена ее с внешними телами. При адиабатическом процессе 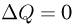 ; теплоемкость вещества в таком процессе равна нулю.
; теплоемкость вещества в таком процессе равна нулю.
Первый закон термодинамики — это закон сохранения энергии, обобщенный на тепловые явления. Согласно этому закону, количество теплоты, полученное системой, расходуется на изменение ее внутренней энергии и на совершение системой работы против внешних сил:
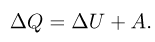
Применение первого закона термодинамики к изотермическому, изохорному и изобарному процессам. Теплоемкость одноатомного идеального газа при изохорном и изобарном процессах
Первый закон термодинамики применительно к изотермическому процессу в идеальном газе имеет вид 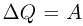 . Внутренняя энергия идеального газа при этом не меняется, поскольку
. Внутренняя энергия идеального газа при этом не меняется, поскольку 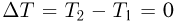 и
и 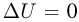 .
.
Вся подведенная теплота расходуется на работу газа против внешнего давления.
При изохорном процессе количество теплоты 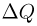 идет только на увеличение внутренней энергии газа:
идет только на увеличение внутренней энергии газа: 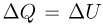 , поскольку работу газ не совершает. Теплоемкость газа в таком процессе называется теплоемкостью при постоянном объеме и обозначается
, поскольку работу газ не совершает. Теплоемкость газа в таком процессе называется теплоемкостью при постоянном объеме и обозначается 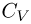 . Для одноатомного идеального газа
. Для одноатомного идеального газа
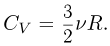
При изобарном процессе количество теплоты, подводимое к газу, расходуется и на увеличение внутренней энергии, и на работу расширения, которую совершает газ против внешнего давления. Поскольку 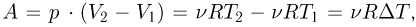 теплоемкость идеального газа в таком процессе, называемая теплоемкостью при постоянном давлении
теплоемкость идеального газа в таком процессе, называемая теплоемкостью при постоянном давлении 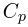 , равна:
, равна:
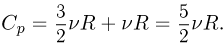
Теплоемкость газа в изобарном процессе превышает его теплоемкость в изохорном процессе на величину работы расширения. Для одного моля идеального газа разность этих теплоемкостей равна универсальной газовой постоянной 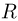 .
.
При адиабатическом процессе первый закон термодинамики принимает вид: 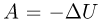 . В отсутствие теплообмена с внешней средой работа, которую совершает газ против внешнего давления, происходит за счет убыли его внутренней энергии. Адиабатически расширяющийся идеальный газ охлаждается.
. В отсутствие теплообмена с внешней средой работа, которую совершает газ против внешнего давления, происходит за счет убыли его внутренней энергии. Адиабатически расширяющийся идеальный газ охлаждается.
Необратимость процессов в природе
В термодинамике большую роль играет понятие обратимого процесса. Обратимым процессом называется такое изменение состояния термодинамической системы, которое, будучи проведено в обратном направлении, возвращает ее в исходное состояние так, чтобы система прошла через те же промежуточные состояния, что и в прямом процессе, но обратной последовательности, а состояние всех тел вне системы, с которыми она взаимодействовала, осталось в итоге неизменным. Важно, что при совершении обратимого процесса сначала в прямом, а затем в обратном направлении в исходное состояние возвращается не только система, но все внешние тела, взаимодействовавшие с системой. Необходимым и достаточным условием обратимости термодинамического процесса является его равновесность.
Равновесный процесс — это идеализированный процесс, при проведении которого в каждый момент не нарушается равновесие термодинамической системы. Он может быть представлен как непрерывная последовательность равновесных состояний. Это означает, что процесс должен быть медленным по сравнению с процессами установления термодинамического равновесия в системе. Строго говоря, только бесконечно медленные процессы являются равновесными.
Все реальные термодинамические процессы протекают с конечной скоростью и поэтому являются неравновесными. Они сопровождаются трением, диффузией и теплообменом с внешней средой при конечной разности температур системы и внешней среды. Следовательно, все реальные процессы необратимы.
Второй закон термодинамики
Многочисленные наблюдения позволили установить, что тепловым процессам присуща определенная направленность, которая не вытекает из первого закона термодинамики. Например, в результате теплообмена между по-разному нагретыми телами всегда происходит выравнивание их температур, хотя с точки зрения первого закона термодинамики одинаково возможен как переход теплоты от более нагретого тела к менее нагретому, так и обратный переход. Первый закон термодинамики формально допускает создание вечного двигателя второго рода. Так называется двигатель, в котором рабочее тело, совершая круговой процесс, получает энергию в форме теплоты от одного внешнего тела и целиком передает ее в форме работы другому внешнему телу.
Невозможность создания вечного двигателя второго рода является утверждением, вытекающим из обобщения многочисленных опытов. Оно называется вторым законом термодинамики и имеет несколько эквивалентных формулировок. Приведем одну из них:
Невозможен периодический процесс, единственным результатом которого является превращение всей теплоты, полученной от нагревателя, в эквивалентную ей работу.
Второй закон термодинамики указывает на необратимость процесса превращения работы в теплоту. В формулировке этого закона особое значение имеют слова «единственным результатом». Запреты, которые накладываются вторым законом термодинамики, снимаются, если процессы, о которых идет речь, не являются единственными. Например, передача тепла от менее нагретого тела более нагретому возможна, если при этом происходит как минимум еще один процесс (в холодильной установке).
Физические основы работы тепловых двигателей. КПД теплового двигателя и его максимальное значение
Тепловым двигателем называется устройство, которое превращает внутреннюю энергию топлива в механическую энергию. Энергия, которая выделяется при сгорании топлива, передается путем теплообмена рабочему телу (обычно газу). При расширении рабочего тела совершается работа против внешних сил и приводится в движение соответствующий механизм.
Основой тепловых двигателей являются круговые процессы. Круговым процессом, или циклом называется термодинамический процесс, в результате которого рабочее тело (возвращается в исходное состояние. На диаграммах состояния  — диаграммах) циклические процессы изображаются в виде замкнутых кривых.
— диаграммах) циклические процессы изображаются в виде замкнутых кривых.
Работа против внешнего давления, которую совершает рабочее тело в произвольном круговом процессе, измеряется площадью, ограниченной кривой этого процесса на 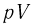 — диаграмме. Прямым циклом называется круговой процесс, в котором рабочее тело совершает положительную работу за счет сообщенной ему теплоты. На
— диаграмме. Прямым циклом называется круговой процесс, в котором рабочее тело совершает положительную работу за счет сообщенной ему теплоты. На 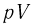 — диаграмме прямой цикл изображается замкнутой кривой, которая обходится по часовой стрелке. Обратным циклом называется круговой процесс, в котором над рабочим телом совершается работа и от него отводится эквивалентное количество теплоты. На
— диаграмме прямой цикл изображается замкнутой кривой, которая обходится по часовой стрелке. Обратным циклом называется круговой процесс, в котором над рабочим телом совершается работа и от него отводится эквивалентное количество теплоты. На 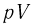 — диаграмме обратный цикл изображается замкнутой кривой, которая обходится против часовой стрелки.
— диаграмме обратный цикл изображается замкнутой кривой, которая обходится против часовой стрелки.
В тепловом двигателе рабочее тело совершает прямой цикл, а в холодильной установке — обратный.
Циклом Карно называется прямой обратимый круговой процесс (рис. 2.2.3), состоящий из двух изотерм 1 — 2 и 3 — 4 и двух адиабат 2 — 3 и 4—1. При изотермическом расширении 1 — 2 рабочее тело получает от нагревателя — источника энергии с постоянной температурой 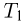 — количество теплоты
— количество теплоты 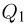 . При изотермическом сжатии 3 — 4 рабочее тело отдает холодильнику, имеющему постоянную температуру
. При изотермическом сжатии 3 — 4 рабочее тело отдает холодильнику, имеющему постоянную температуру 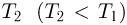 , количество теплоты
, количество теплоты 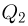 . При адиабатических расширении и сжатии энергия к рабочему телу извне не поступает и эти процессы происходят за счет изменения его внутренней энергии.
. При адиабатических расширении и сжатии энергия к рабочему телу извне не поступает и эти процессы происходят за счет изменения его внутренней энергии.
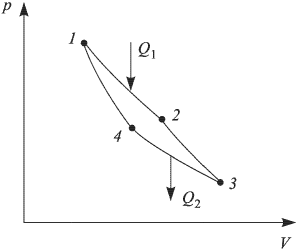
Коэффициентом полезного действия (КПД) произвольного цикла называется отношение работы 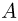 , совершенной рабочим телом в прямом цикле, к количеству теплоты
, совершенной рабочим телом в прямом цикле, к количеству теплоты 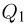 , сообщенному рабочему телу нагревателем:
, сообщенному рабочему телу нагревателем:
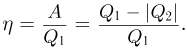
КПД обратимого цикла Карно не зависит от природы рабочего тела и определяется только температурами нагревателя 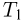 , и холодильника
, и холодильника 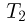 :
:
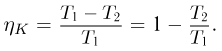
Согласно теореме Карно, КПД произвольного обратимого цикла не может превышать КПД обратимого цикла Карно, осуществленного с теми же температурами 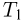 и
и 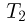 нагревателя и холодильника. КПД произвольного необратимого цикла всегда меньше КПД обратимого цикла Карно, проведенного между температурами
нагревателя и холодильника. КПД произвольного необратимого цикла всегда меньше КПД обратимого цикла Карно, проведенного между температурами 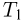 и
и 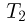 .
.
Любой тепловой двигатель, независимо от его конструктивных особенностей, состоит из трех основных частей: рабочего тела, нагревателя и холодильника (рис. 2.2.4). Рабочее тело — газ или пар — при расширении совершает работу, получая от нагревателя некоторое количество теплоты 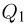 . Температура
. Температура 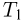 нагревателя остается при этом постоянной за счет сгорания топлива. При сжатии рабочее тело передает некоторое количество теплоты
нагревателя остается при этом постоянной за счет сгорания топлива. При сжатии рабочее тело передает некоторое количество теплоты 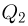 холодильнику — телу постоянной температуры
холодильнику — телу постоянной температуры 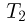 , меньшей, чем
, меньшей, чем 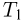 .
.
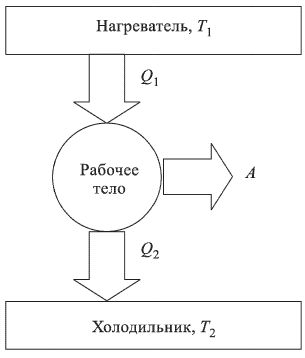
Давление газа при сжатии ниже, чем при расширении, что обеспечивает полезную работу двигателя.
Реальные тепловые двигатели работают по разомкнутому циклу: после расширения газ выбрасывается, и сжимается новая порция. Однако, тепловые процессы в рассмотренном выше замкнутом цикле, когда сжимается и расширяется одна и та же порция газа, являются хорошей аппроксимацией для процессов в реальном двигателе, и могут быть использованы для расчета его КПД.
Указания по решению задач
При решении задач важно иметь в виду, что количество теплоты, полученное или отданное газом в некотором процессе, зависит не только от начального и конечного состояний газа, но и от вида самого процесса, поскольку вид процесса определяет работу, совершенную газом. Поэтому часто говорят, что количество теплоты — это не функция состояния, а функция процесса. В то же время, внутренняя энергия однозначно определяется состоянием газа, поэтому ее изменение не зависит от вида процесса. В частности, в циклическом процессе полное изменение внутренней энергии равно нулю и работа, совершенная газом за цикл, равна алгебраической сумме всех количеств теплоты, полученных и отданных газом в этом процессе.
Примеры решения задач №2:
Задача №2.2.1.
В сосуде емкостью 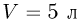 находится гелий под давлением
находится гелий под давлением 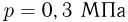 . Какова внутренняя энергия
. Какова внутренняя энергия 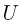 газа в сосуде?
газа в сосуде?
Решение: Из уравнения состояния газа 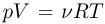 находим его температуру:
находим его температуру: 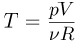 . Поскольку гелий — одноатомный газ, его внутренняя энергия
. Поскольку гелий — одноатомный газ, его внутренняя энергия 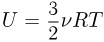 . Ответ:
. Ответ: 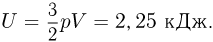
Задача №2.2.2.
Газ, взятый в количестве 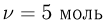 , сначала нагревают при постоянном объеме так, что абсолютная температура газа возрастает в
, сначала нагревают при постоянном объеме так, что абсолютная температура газа возрастает в 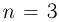 раза, а затем сжимают при постоянном давлении, доводя температуру до первоначальной
раза, а затем сжимают при постоянном давлении, доводя температуру до первоначальной 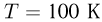 . Какая работа
. Какая работа 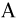 совершена при сжатии? Универсальная газовая постоянная
совершена при сжатии? Универсальная газовая постоянная 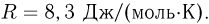
Решение:
График процесса изображен на рисунке. Поскольку величина работы, совершенной над газом, численно равна площади под кривой зависимости давления от объема, в нашем случае имеем:
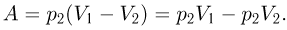
Из уравнения состояния газа следует, что
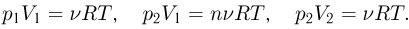
Объединяя записанные выражения, получаем ответ:
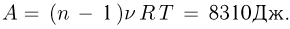
Задача №2.2.3.
С массой 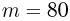 г идеального газа, молярная масса которого
г идеального газа, молярная масса которого 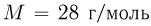 , совершается циклический процесс, изображенный на рисунке. Какую работу
, совершается циклический процесс, изображенный на рисунке. Какую работу 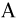 совершает такой двигатель за один цикл? Универсальную газовую постоянную принять
совершает такой двигатель за один цикл? Универсальную газовую постоянную принять 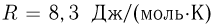 ,
, 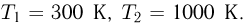 При нагревании на участке 4 — 1 давление газа увеличивается в 2 раза.
При нагревании на участке 4 — 1 давление газа увеличивается в 2 раза.
Решение:
Для вычисления работы газа удобно перерисовать график процесса в виде  — диаграммы (см. рисунок), откуда видно, что
— диаграммы (см. рисунок), откуда видно, что
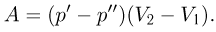
Используя уравнение состояния газа, запишем последнее равенство в виде: 
Поскольку объемы газа на участках 2 — 3 и 4 — 1 постоянны, имеем:
Отсюда  Подставляя найденные значения температуры в выражение для работы, получаем ответ:
Подставляя найденные значения температуры в выражение для работы, получаем ответ:
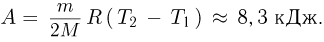
Задача №2.2.4.
Найти работу, совершенную идеальным газом за цикл (см. рисунок). Объем 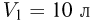 , давление
, давление 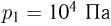 . Давление
. Давление 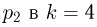 раза превышает
раза превышает 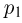 . Температура в точках 2 и 4 одинакова.
. Температура в точках 2 и 4 одинакова.
Решение:
Работа газа за цикл равна площади трапеции:
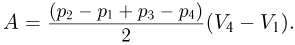
Из подобия треугольников следует, что
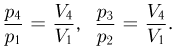
Поскольку точки 2 и 4 находятся на одной изотерме, 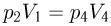 . Кроме того, по условию
. Кроме того, по условию 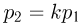 . Объединяя эти соотношения, получаем:
. Объединяя эти соотношения, получаем:
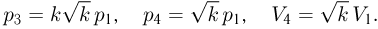
Подставляя эти выражения в формулу для работы, находим ответ:
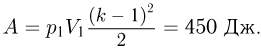
Задача №2.2.5.
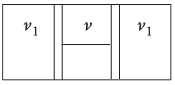
Горизонтально расположенный цилиндр разделен двумя подвижными поршнями, связанными нитью, на три равные части объемом 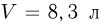 каждая. В центральной части находится
каждая. В центральной части находится 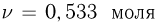 гелия, а в левой и правой частях — по
гелия, а в левой и правой частях — по 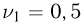 молей азота
молей азота 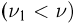 . Температура всех газов равна
. Температура всех газов равна 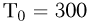 K. Когда гелию сообщили количество теплоты
K. Когда гелию сообщили количество теплоты 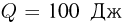 , поддерживая температуру азота постоянной, нить оборвалась. Найти максимальное натяжение
, поддерживая температуру азота постоянной, нить оборвалась. Найти максимальное натяжение 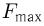 , которое выдерживает нить. Площади поршней
, которое выдерживает нить. Площади поршней 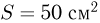 , универсальная газовая постоянная
, универсальная газовая постоянная 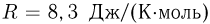 . Трение между поршнями и цилиндром пренебрежимо мало.
. Трение между поршнями и цилиндром пренебрежимо мало.
Решение:
Поскольку нагрев гелия происходит при постоянном объеме, сообщенное ему количество тепла идет на увеличение его внутренней энергии: 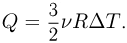 Следовательно, изменение его температуры
Следовательно, изменение его температуры
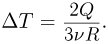
Давление азота 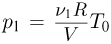 , давление гелия после нагревания р
, давление гелия после нагревания р 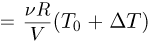 . Из условия равновесия поршней следует, что сила натяжения нити
. Из условия равновесия поршней следует, что сила натяжения нити 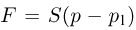 . Объединяя записанные выражения, получаем ответ:
. Объединяя записанные выражения, получаем ответ: 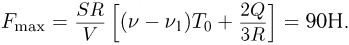
Задача №2.2.6.
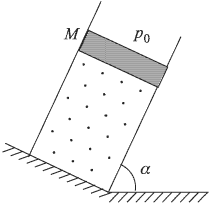
В закрепленном под углом 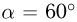 к горизонту цилиндре может без трения двигаться поршень массой
к горизонту цилиндре может без трения двигаться поршень массой 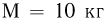 и площадью
и площадью 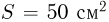 . Под поршнем находится одноатомный идеальный газ. Газ нагревают так, что поршень перемещается на расстояние
. Под поршнем находится одноатомный идеальный газ. Газ нагревают так, что поршень перемещается на расстояние 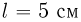 . Какое количество теплоты
. Какое количество теплоты 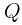 было сообщено газу? Атмосферное давление
было сообщено газу? Атмосферное давление 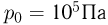 , ускорение свободного падения принять
, ускорение свободного падения принять 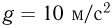 .
.
Решение:
При нагревании газ перемещает поршень, совершая изобарное расширение. Используя для молярной теплоемкости одноатомного идеального газа при постоянном давлении известное выражение:
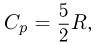
находим, что количество теплоты, сообщенное газу, равно
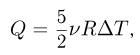
где  — число молей газа,
— число молей газа, 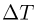 — изменение его температуры в рассматриваемом процессе. Записывая уравнения начального и конечного состояний газа, имеем
— изменение его температуры в рассматриваемом процессе. Записывая уравнения начального и конечного состояний газа, имеем
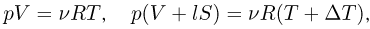
где 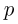 — давление газа,
— давление газа, 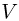 — начальный объем газа,
— начальный объем газа, 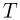 — его начальная температура. Отсюда
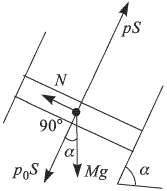
— его начальная температура. Отсюда 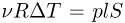 . Для определения давления газа воспользуемся условием механического равновесия поршня под действием сил, изображенных на рисунке:
. Для определения давления газа воспользуемся условием механического равновесия поршня под действием сил, изображенных на рисунке:
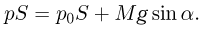
Объединяя записанные выражения, получаем ответ:
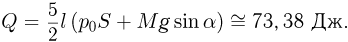
Задача №2.2.7.
Некоторое количество одноатомного идеального газа нужно перевести из состояния 1 в состояние 2, используя изохорный и изобарный процессы (см. рисунок). Во сколько раз 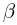 отличаются количества теплоты, которые требуются для перехода из исходного в конечное состояние по путям 1-3-2 и 1-4-2 соответственно?
отличаются количества теплоты, которые требуются для перехода из исходного в конечное состояние по путям 1-3-2 и 1-4-2 соответственно?
Решение:
Проведем расчет количеств теплоты на отдельных участках. С учетом уравнения состояния газа имеем:
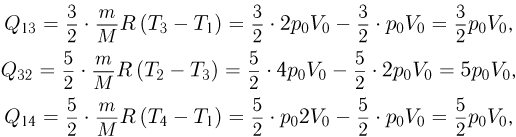
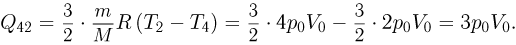
Отсюда
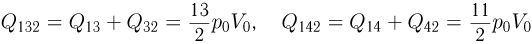
Ответ: 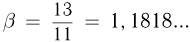
Задача №2.2.8.
Найти количество тепла 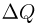 , переданное одноатомному газу при переводе его из состояния 1 в состояние 2 как показано на рисунке. При расчете принять
, переданное одноатомному газу при переводе его из состояния 1 в состояние 2 как показано на рисунке. При расчете принять 
Решение:
Изменение внутренней энергии в рассматриваемом процессе 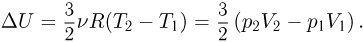
Учитывая, что продолжение прямой, изображающей график процесса, проходит через начало координат (давление в этом процессе пропорционально объему), имеем: 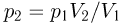 . Следовательно,
. Следовательно,
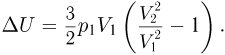
Работа газа в этом процессе численно равна площади трапеции:
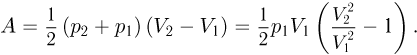
Количество тепла, полученное газом,
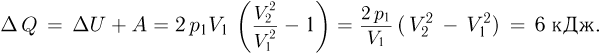
Задача №2.2.9.
Два сосуда содержат одноатомный идеальный газ. Масса газа в первом сосуде 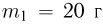 , его температура
, его температура 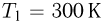 . Второй сосуд содержит такой же газ массой
. Второй сосуд содержит такой же газ массой 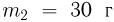 при температуре
при температуре 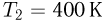 . Сосуды соединяют трубкой. Пренебрегая объемом трубки и теплообменом с окружающей средой, найти температуру газа
. Сосуды соединяют трубкой. Пренебрегая объемом трубки и теплообменом с окружающей средой, найти температуру газа 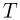 , установившуюся в сосудах.
, установившуюся в сосудах.
Решение:
Поскольку сосуды теплоизолированы и газ не совершает работу, внутренняя энергия газа в этом процессе остается постоянной. Следовательно,
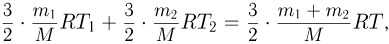
где 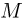 — молярная масса газа. Отсюда
— молярная масса газа. Отсюда 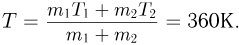
Задача №2.2.10.
В вертикально расположенном цилиндрическом сосуде, площадь сечения которого 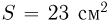 , под поршнем весом
, под поршнем весом 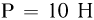 находится одноатомный газ. Расстояние между дном сосуда и поршнем
находится одноатомный газ. Расстояние между дном сосуда и поршнем 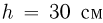 . На внутренней стенке сосуда имеется стопорное кольцо, не позволяющее расстоянию между дном сосуда и поршнем превысить величину
. На внутренней стенке сосуда имеется стопорное кольцо, не позволяющее расстоянию между дном сосуда и поршнем превысить величину 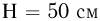 . Какое количество тепла
. Какое количество тепла 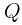 нужно сообщить газу, чтобы его давление увеличилось в
нужно сообщить газу, чтобы его давление увеличилось в 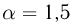 раза? Атмосферное давление
раза? Атмосферное давление 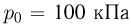 .
.
Решение:
До тех пор, пока поршень не достигнет стопорного кольца, расширение газа при нагревании будет происходить при постоянном давлении 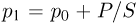 . Записывая уравнения состояния газа в начальный момент и в момент, когда поршень достигает стопорного кольца, имеем:
. Записывая уравнения состояния газа в начальный момент и в момент, когда поршень достигает стопорного кольца, имеем: 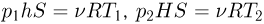 .
.
Отсюда, изменение температуры в этом процессе:
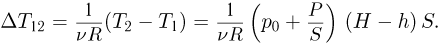
Соответственно, полученное в этом процессе газом тепло:
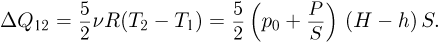
При дальнейшем нагревании объем газа не меняется, т.к. стопорное кольцо препятствует перемещению поршня. В конечном состоянии газа его давление 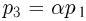 . Из уравнения этого состояния
. Из уравнения этого состояния 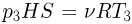 находим температуру
находим температуру
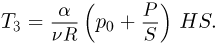
Количество тепла, полученное газом в этом процессе:
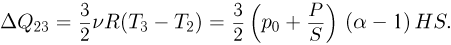
Учитывая, что 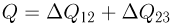 , получаем ответ:
, получаем ответ:
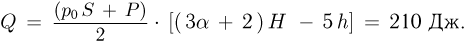
Задача №2.2.11.
С одним молем идеального газа проводят циклический процесс, состоящий из двух изохор и двух изобар. Найти работу 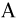 , совершаемую газом за цикл, если известно, что температура в состоянии 1
, совершаемую газом за цикл, если известно, что температура в состоянии 1
 , а в состояниях 2 и 4 температура одинакова и равна
, а в состояниях 2 и 4 температура одинакова и равна  . Универсальная газовая постоянная
. Универсальная газовая постоянная  .
.
Решение:
Работа газа в циклическом процессе численно равна площади, ограниченной графиком процесса на  — диаграмме. Вводя для
— диаграмме. Вводя для
давлений и объемов газа в характерных точках цикла обозначения, приведенные на рисунке, имеем
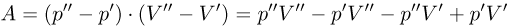
Используя для газа в состояниях 1, 2, 3, 4 уравнение Клапейрона-Менделеева и учитывая, что количество газа  , можно переписать выражение для работы газа в виде
, можно переписать выражение для работы газа в виде
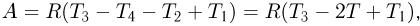
где 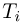 — температура газа в состоянии
— температура газа в состоянии 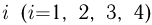 , причем по условию
, причем по условию 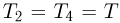 . Поскольку процессы 1 — 2 и 3 — 4 проводятся при постоянных объемах,
. Поскольку процессы 1 — 2 и 3 — 4 проводятся при постоянных объемах,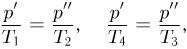
откуда следует, что 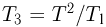 . Используя последнее выражение, получаем ответ:
. Используя последнее выражение, получаем ответ: 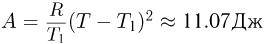 .
.
Задача №2.2.12.
В вертикально расположенном цилиндрическом сосуде под поршнем весом 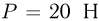 содержится идеальный одноатомный газ.Между поршнем и неподвижной опорой располагается пружина, жесткость которой
содержится идеальный одноатомный газ.Между поршнем и неподвижной опорой располагается пружина, жесткость которой 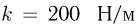 . Расстояние между поршнем и
. Расстояние между поршнем и
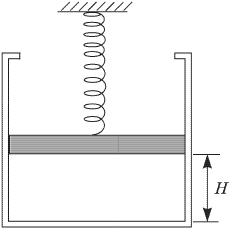
дном сосуда 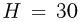 см, при этом пружина не деформирована. Какое количество тепла
см, при этом пружина не деформирована. Какое количество тепла 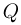 нужно сообщить газу, чтобы поршень переместился на расстояние
нужно сообщить газу, чтобы поршень переместился на расстояние 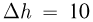 см? Атмосферное давление не учитывать.
см? Атмосферное давление не учитывать.
Решение:
При нагревании газ будет расширяться, совершая работу по подъему поршня и сжатию пружины:
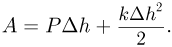
Одновременно будет повышаться температура газа, изменение которой в этом процессе легко найти из уравнений начального и конечного состояний газа. Учитывая, что давления газа в этих состояниях равны, соответственно 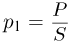 и
и 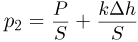 , имеем:
, имеем:
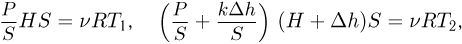
откуда
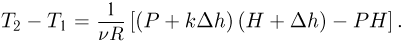
Поскольку 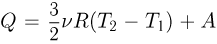 , после несложных преобразований получаем ответ
, после несложных преобразований получаем ответ 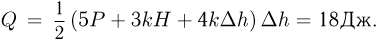
Задача №2.2.13.
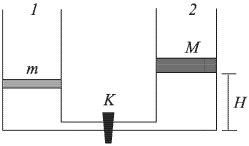
В цилиндрическом сосуде 1 под поршнем массой 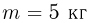 находится одноатомный идеальный газ. Сосуд 1 соединен трубкой, снабженной краном, с таким же сосудом 2, в котором под поршнем массой
находится одноатомный идеальный газ. Сосуд 1 соединен трубкой, снабженной краном, с таким же сосудом 2, в котором под поршнем массой 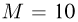 кг находится такой же газ. Сосуды и трубка теплоизолированы. В начальном состоянии кран
кг находится такой же газ. Сосуды и трубка теплоизолированы. В начальном состоянии кран 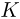 закрыт, температура газа в обоих сосудах одинакова, поршень в сосуде 2 расположен на высоте
закрыт, температура газа в обоих сосудах одинакова, поршень в сосуде 2 расположен на высоте 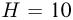 см от дна. На какое расстояние
см от дна. На какое расстояние 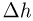 передвинется поршень в сосуде 1 после открывания крана? Объемом трубки с краном пренебречь, атмосферное давление не учитывать.
передвинется поршень в сосуде 1 после открывания крана? Объемом трубки с краном пренебречь, атмосферное давление не учитывать.
Решение:
При закрытом кране внутренние энергии газов в сосудах 1 и 2 равны, соответственно:
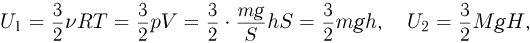 где
где 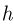 — первоначальная высота поршня в сосуде 1. После открывания крана более тяжелый поршень, находящийся в сосуде 2, опустится на дно, полностью вытеснив газ в сосуд 1. В результате этого поршень в сосуде 1 поднимется на высоту
— первоначальная высота поршня в сосуде 1. После открывания крана более тяжелый поршень, находящийся в сосуде 2, опустится на дно, полностью вытеснив газ в сосуд 1. В результате этого поршень в сосуде 1 поднимется на высоту 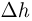 и внутренняя энергия газа в этом сосуде станет равной
и внутренняя энергия газа в этом сосуде станет равной 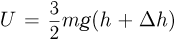 . Таким образом, изменение внутренней энергии в системе
. Таким образом, изменение внутренней энергии в системе
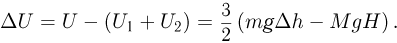
Работа, совершенная системой и над системой в сумме равна:
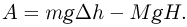
Поскольку система теплоизолирована, 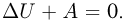 Объединяя записанные выражения, получаем ответ:
Объединяя записанные выражения, получаем ответ: 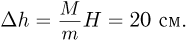
Задача №2.2.14.
С одним молем идеального газа проводят циклический процесс, состоящий из двух изохор и двух изобар. Найти коэффициент полезного действия цикла 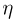 , если известно, что температура в состоянии
, если известно, что температура в состоянии 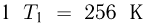 , в состоянии
, в состоянии 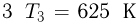 , а в состояниях 2 и 4 температура одинакова. Универсальная газовая постоянная
, а в состояниях 2 и 4 температура одинакова. Универсальная газовая постоянная 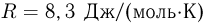 .
.
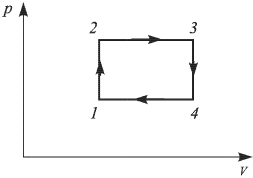
Решение:
Работа газа в циклическом процессе равна (см. обозначения, приведенные на рисунке):
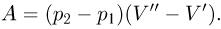
Обозначив через 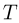 температуру газа в точках 2 и 4 и используя уравнение Клапейрона-Менделеева, преобразуем это выражение к виду:
температуру газа в точках 2 и 4 и используя уравнение Клапейрона-Менделеева, преобразуем это выражение к виду:
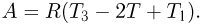
Поскольку отношения давлений в точках 1, 2 и 3, 4 одинаковы и процессы 1—2 и 3 — 4 проводятся при постоянных объемах, для
температур в этих точках справедливо равенство: 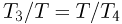 . Отсюда
. Отсюда 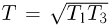 . Простой анализ показывает, что приращения тепла в данном циклическом процессе положительны на участках 1 — 2 и 2 — 3. Поэтому количество тепла, полученное газом в цикле, равно
. Простой анализ показывает, что приращения тепла в данном циклическом процессе положительны на участках 1 — 2 и 2 — 3. Поэтому количество тепла, полученное газом в цикле, равно
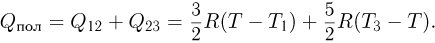
Учитывая, что КПД цикла 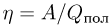 , после несложных преобразований получаем ответ:
, после несложных преобразований получаем ответ: 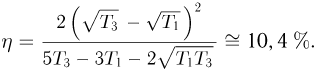
Изменение агрегатного состояния вещества. Определения, понятия и законы
В различных интервалах температур и давлений большинство веществ может находиться в разных состояниях — газообразном, жидком и твердом. Эти состояния вещества называются агрегатными. Молекулярно-кинетическая теория позволяет объяснить процесс перехода вещества из одного агрегатного состояния в другое.
Парообразование. Испарение. Насыщенный пар. Зависимость плотности и давления насыщенного пара от температуры
Взаимные превращения жидкостей и газов описываются процессами парообразования и конденсации. Парообразованием называется процесс перехода вещества из жидкого состояния в газообразное. Парообразование, происходящее при любой температуре со свободной поверхности жидкости, называется испарением. Совокупность молекул, вылетевших из жидкости при парообразовании, называется паром данной жидкости. Образование пара происходит не только у жидкостей, но и у твердых тел.
Из поверхностного слоя жидкости вылетают молекулы, которые обладают наибольшей скоростью и, следовательно, кинетической энергией теплового движения, поэтому в результате испарения жидкость охлаждается.
Если процесс парообразования происходит в закрытом сосуде, то по истечении некоторого времени количество жидкости перестает убывать, хотя молекулы жидкости, способные покинуть ее поверхность, продолжают переходить в пар. В этом случае, наряду с процессом парообразования, определяющую роль начинает играть компенсирующий его обратный процесс — конденсация, т.е. превращение пара в жидкость. Концентрация вещества в газообразном состоянии достигает такого значения, при котором число молекул, возвращающихся в жидкость, становится равным числу молекул, покидающих поверхность жидкости за то же время, иными словами, становятся равными скорости парообразования и конденсации. Устанавливается динамическое равновесие между процессами испарения и конденсации. Пар, находящийся в состоянии динамического равновесия со своей жидкостью, называется насыщенным паром. Пар, находящийся при давлении ниже давления насыщенного пара, является ненасыщенным.
Давление насыщенного пара 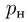 зависит только от его химического состава и температуры и не зависит от величины свободного от жидкости объема сосуда, в котором находится пар. Это объясняется тем, что при сжатии насыщенного пара концентрация молекул пара увеличивается, равновесие между процессами испарения и конденсации нарушается и часть пара превращается в жидкость. При расширении насыщенного пара наоборот часть жидкости превращается в пар.
зависит только от его химического состава и температуры и не зависит от величины свободного от жидкости объема сосуда, в котором находится пар. Это объясняется тем, что при сжатии насыщенного пара концентрация молекул пара увеличивается, равновесие между процессами испарения и конденсации нарушается и часть пара превращается в жидкость. При расширении насыщенного пара наоборот часть жидкости превращается в пар.
Интенсивность процесса испарения увеличивается с возрастанием температуры жидкости. Поэтому динамическое равновесие между испарением и конденсацией при повышении температуры устанавливается при больших концентрациях молекул пара, т.е. при больших его давлениях.
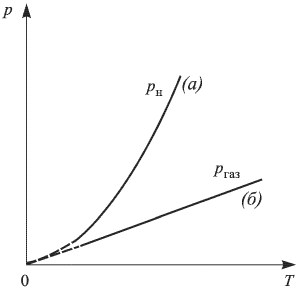
Давление идеального газа при постоянной концентрации молекул возрастает прямо пропорционально абсолютной температуре. Так как в насыщенном паре при возрастании температуры концентрация молекул увеличивается, давление насыщенного пара с повышением температуры возрастает быстрее, чем давление идеального газа с постоянной концентрацией молекул (рис. 2.3.1).
Кипение
Процесс парообразования может происходить не только с поверхности жидкости, но и внутри жидкости. Если давление насыщенного пара равно давлению в жидкости или превышает его, пузырьки пара внутри жидкости расширяются и всплывают на поверхность. Процесс интенсивного парообразования не только со свободной поверхности жидкости, но и по всему ее объему внутрь образующихся при этом пузырьков пара, называется кипением.
Зависимость температуры кипения от давления
Температурой (точкой)кипения называется температура жидкости, при которой давление ее насыщенного пара равно внешнему давлению. При понижении внешнего давления температура кипения жидкости понижается, при повышении давления — повышается. В частности, при температуре 100 °C давление насыщенного водяного пара равно нормальному атмосферному давлению и кипение воды происходит при 100 °C. Если давление над водой уменьшить до половины нормального атмосферного давления, вода закипит при 80 °C. При давлении, в 2 раза превышающем нормальное атмосферное давление, температура кипения воды равна 120 °C.
Удельная теплота парообразования
Если внешнее давление не изменяется, в процессе кипения температура жидкости остается постоянной. Теплота, которая извне подводится к жидкости, расходуется на парообразование. Количество теплоты г, необходимое для превращения в пар единицы массы жидкости, нагретой до температуры кипения, называется удельной теплотой парообразования. Из закона сохранения энергии следует, что при обратном процессе — конденсации пара в жидкость — выделяется то же количество теплоты.
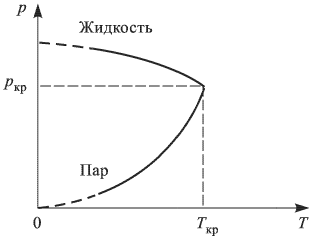
Критическая температура
При увеличении температуры жидкости увеличивается давление насыщенного пара и одновременно растет его плотность. Плотность жидкости, находящейся в равновесии со своим паром, уменьшается вследствие теплового расширения. Графики зависимости от температуры плотностей насыщенного пара и жидкости пересекаются в некоторой точке, называемой критической (рис. 2.3.2). В критической точке плотность жидкости равна плотности насыщенного пара, находящегося в равновесии с жидкостью. При критической температуре плотность и давление насыщенного пара становятся максимальными, а плотность жидкости, находящейся в равновесии с паром, минимальной. Критическая температура для воды 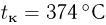 .
.
Особое значение критической температуры состоит в том, что при температуре выше критической газ нельзя превратить в жидкость ни при каких давлениях.
Влажность. Относительная влажность
Содержание водяного пара в воздухе можно характеризовать несколькими величинами. Абсолютной влажностью воздуха (или просто влажностью воздуха) р называют плотность водяных паров, содержащихся в воздухе при данных условиях. Обычно влажность выражают в 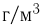 . Поскольку в атмосферном воздухе интенсивность испарения воды зависит от того, насколько близко давление паров воды к давлению насыщенных паров при данной температуре, важно также знать относительную влажность. Относительной влажностью воздуха
. Поскольку в атмосферном воздухе интенсивность испарения воды зависит от того, насколько близко давление паров воды к давлению насыщенных паров при данной температуре, важно также знать относительную влажность. Относительной влажностью воздуха 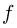 называется отношение парциального давления водяного пара
называется отношение парциального давления водяного пара 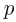 , содержащегося в воздухе при данной температуре, к давлению
, содержащегося в воздухе при данной температуре, к давлению 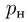 насыщенного водяного пара при той же температуре, выраженное в процентах:
насыщенного водяного пара при той же температуре, выраженное в процентах:
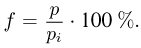
Так как давление насыщенного пара тем меньше, чем ниже температура, то при охлаждении воздуха находящийся в нем водяной пар при некоторой температуре становится насыщенным. Температура  , при которой находящийся в воздухе водяной пар становится насыщенным, называется точкой росы. При температуре воздуха, равной, или более низкой, чем точка росы, испарение воды прекращается.
, при которой находящийся в воздухе водяной пар становится насыщенным, называется точкой росы. При температуре воздуха, равной, или более низкой, чем точка росы, испарение воды прекращается.
Кристаллическое и аморфное состояния вещества. Твердые тела по своим свойствам и внутреннему строению делятся на кристаллические и аморфные.
Кристаллы — это твердые тела, атомы или молекулы которых занимают определенные, упорядоченные положения в пространстве. Кристаллические твердые тела обладают анизотропией — зависимостью физических свойств от направления внутри кристалла. К числу таких свойств относятся механическая прочность, коэффициент теплового расширения, электро- и теплопроводность, показатель преломления света и пр.
Различаются следующие четыре типа твердых кристаллов:
- Ионные кристаллы — большинство неорганических соединений, например соли (NaCl и др.), окиси металлов и т.д. В узлах кристаллических решеток ионных кристаллов размещаются правильно чередующиеся положительные и отрицательные ионы, между которыми действуют главным образом силы электростатического взаимодействия, осуществляющие ионную связь. В процессе кристаллизации одни атомы (например, Na) теряют электроны, которые присоединяются к другим атомам (например, Cl), и возникают два противоположно заряженных иона.
- Атомные (валентные) кристаллы — кристаллические решетки полупроводников (Те, Ge и др.), многие органические твердые тела. Типичными примерами таких кристаллов являются разновидности углерода — алмаз и графит. В узлах кристаллических решеток атомных кристаллов находятся электрически нейтральные атомы, чаще всего одинаковые, между которыми осуществляется особая ковалентная связь, имеющая квантовомеханическое происхождение.
- Молекулярные кристаллы —
 нафталин, парафин, многие твердые органические соединения. В узлах кристаллических решеток таких кристаллов находятся молекулы, сохраняющие свою «индивидуальность». Между этими молекулами действуют силы притяжения, характерные для взаимодействия молекул. Относительно малая устойчивость молекулярных кристаллов, их низкие температуры плавления объясняются тем, что силы притяжения между их молекулами меньше, чем у кристаллов других типов.
нафталин, парафин, многие твердые органические соединения. В узлах кристаллических решеток таких кристаллов находятся молекулы, сохраняющие свою «индивидуальность». Между этими молекулами действуют силы притяжения, характерные для взаимодействия молекул. Относительно малая устойчивость молекулярных кристаллов, их низкие температуры плавления объясняются тем, что силы притяжения между их молекулами меньше, чем у кристаллов других типов. - Металлические кристаллы (металлы). При кристаллизации металлов происходит отщепление от атомов внешних (валентных) электронов и образуются положительные ионы, которые располагаются в узлах кристаллической решетки. Валентные электроны становятся «коллективизированными» — они принадлежат всему кристаллу в целом, образуя электронный газ. Металлическая связь в кристаллической решетке металлов обеспечивается притяжением между положительно заряженными ионами, находящимися в узлах кристаллической решетки, и отрицательно заряженным электронным газом. Коллективизированные электроны металлов как бы «стягивают» положительные ионы, уравновешивая отталкивание между ними. При расстояниях между ионами, равных периоду кристаллической решетки, возникает устойчивая конфигурация ионов. Наличием электронного газа объясняется хорошая электропроводность металлов.
Кристаллические тела делятся на монокристаллы и поликристаллы. Монокристаллы часто обладают геометрически правильной внешней формой, но главный признак монокристалла — периодически повторяющаяся внутренняя структура во всем объеме. Поликристаллическое тело представляет собой совокупность сросшихся друг с другом хаотически ориентированных маленьких кристаллов. Каждый маленький монокристалл анизотропен, но поликристаллическое тело, как правило, изотропно.
Наряду с кристаллическими, в природе существуют также аморфные тела. У аморфных тел нет строгого порядка в расположении атомов. Все аморфные тела изотропны, т.е. их физические свойства одинаковы по всем направлениям. К аморфным телам относятся стекло, смола, канифоль, плавленый сахар и др. При внешних воздействиях аморфные тела обнаруживают одновременно упругие свойства, подобно кристаллам, и текучесть, подобно жидкости. Упругие свойства аморфных тел проявляются при низких температурах. При повышении температуры они постепенно размягчаются и по свойствам все более приближаются к жидкостям. Определенной температуры плавления у аморфных тел, в отличие от кристаллических, нет.
Удельная теплота плавления
Взаимные превращения кристаллических твердых тел и жидкостей описываются процессами плавления и кристаллизации (отвердевания). Плавлением твердых тел называется их переход из твердого состояния в жидкое. В результате плавления происходит разрушение кристаллической решетки твердого тела. Плавление происходит при определенной температуре, называемой температурой (точкой) плавления  . Как правило, плавление твердых тел сопровождается уменьшением плотности. Исключение составляют лед и висмут, у которых плавление сопровождается увеличением плотности.
. Как правило, плавление твердых тел сопровождается уменьшением плотности. Исключение составляют лед и висмут, у которых плавление сопровождается увеличением плотности.
В процессе плавления твердого тела оно существует одновременно и в твердом, и в жидком состояниях. Температура тела не изменяется при плавлении и остается все время равной 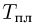 . Все количество теплоты, которое подводится к твердому телу, расходуется на разрушение кристаллической решетки. Количество теплоты, необходимое для перевода единицы массы твердого тела, находящегося при температуре плавления, в жидкое состояние называется удельной теплотой плавления
. Все количество теплоты, которое подводится к твердому телу, расходуется на разрушение кристаллической решетки. Количество теплоты, необходимое для перевода единицы массы твердого тела, находящегося при температуре плавления, в жидкое состояние называется удельной теплотой плавления 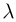 .
.
Переход вещества из жидкого в твердое кристаллическое состояние называется кристаллизацией (затвердеванием). Для любой химически чистой жидкости этот процесс идет при постоянной температуре кристаллизации, которая совпадает с температурой плавления 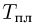 . Кристаллизация единицы массы жидкости сопровождается выделением некоторого количества теплоты — удельной теплоты кристаллизации, — равной удельной теплоте плавления.
. Кристаллизация единицы массы жидкости сопровождается выделением некоторого количества теплоты — удельной теплоты кристаллизации, — равной удельной теплоте плавления.
Уравнение теплового баланса
Если внутри теплоизолированной системы не совершается механической работы, то для нее справедливо уравнение теплового баланса:
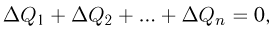
где 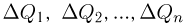 — количества теплоты, полученные (положительные) или отданные (отрицательные) телами системы. Эти количества теплоты рассчитываются по следующим формулам.
— количества теплоты, полученные (положительные) или отданные (отрицательные) телами системы. Эти количества теплоты рассчитываются по следующим формулам.
При изменении температуры тела массы т количество переданной ему теплоты
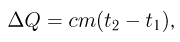
где 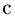 — удельная теплоемкость вещества,
— удельная теплоемкость вещества, 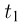 и
и 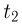 — начальная и конечная температуры.
— начальная и конечная температуры.
При превращении жидкости, находящейся при температуре кипения, в пар количество теплоты, переданной жидкости,
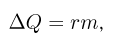
где 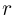 — удельная теплота парообразования. При конденсации пара выделяется такое же количество теплоты.
— удельная теплота парообразования. При конденсации пара выделяется такое же количество теплоты.
Плавление кристаллического тела, нагретого до температуры плавления, требует передачи ему количества теплоты
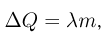
где 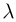 — удельная теплота плавления. При кристаллизации выделяется то же количество теплоты.
— удельная теплота плавления. При кристаллизации выделяется то же количество теплоты.
Указания по решению задач
При решении задач, в которых рассматривается влажность воздуха, следует иметь в виду, что ненасыщенный пар по своей природе ничем не отличается от обычного газа, поэтому для описания его состояния справедливо уравнение Клапейрона-Менделеева. Однако, в состояниях, близких к насыщению, это уравнение в обычной форме становится неприменимым. При рассмотрении процессов, происходящих с насыщенным паром, надо учитывать, что при изменении температуры, давления или объема изменяется также и масса пара. В частности, при изотермическом сжатии масса пара изменяется пропорционально его объему. Следовательно, плотность пара 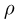 и его давление
и его давление 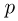 постоянны. Поэтому связь между плотностью и давлением, вытекающая из уравнения
постоянны. Поэтому связь между плотностью и давлением, вытекающая из уравнения 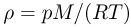 , справедлива и для насыщенного пара.
, справедлива и для насыщенного пара.
В задачах, связанных с изменением агрегатного состояния тел, находящихся в тепловом контакте, для правильной записи уравнения теплового баланса важно детально проследить, через какие промежуточные состояния проходят исходные вещества, прежде чем достигнут конечного состояния термодинамического равновесия. В связи с этим рекомендуется сначала численно оценить количества теплоты, которые могут выделиться ли поглотиться при всех возможных в данной задаче переходах из одного агрегатного состояния в другое, и определить на основании этого, в каких агрегатных состояниях будут находиться все вещества в конечном состоянии. Только после этого имеет смысл записывать уравнение теплового баланса.
Примеры решения задач №3:
Задача №2.3.1.
Относительная влажность воздуха в комнате объемом V = 40 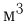 равна
равна 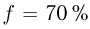 . Найти массу т водяных паров в комнате, если температура воздуха
. Найти массу т водяных паров в комнате, если температура воздуха 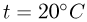 , а давление насыщенного пара при этой температуре
, а давление насыщенного пара при этой температуре 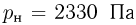 . Универсальная газовая постоянная
. Универсальная газовая постоянная 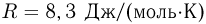 , молярная масса воды
, молярная масса воды 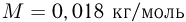 .
.
Решение:
Парциальное давление водяного пара  . Записывая для водяного пара уравнение Клапейрона-Менделева
. Записывая для водяного пара уравнение Клапейрона-Менделева
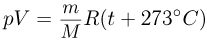 ,
,
получаем ответ: 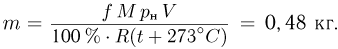
Задача №2.3.2.
В комнате при температуре 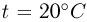 относительная влажность воздуха
относительная влажность воздуха 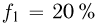 . Какую массу
. Какую массу  воды нужно испарить для увеличения влажности до величины
воды нужно испарить для увеличения влажности до величины 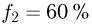 при той же температуре? Объем комнаты
при той же температуре? Объем комнаты 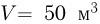 , плотность насыщенных паров воды при температуре
, плотность насыщенных паров воды при температуре 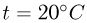 равна
равна 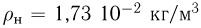 .
.
Решение:
Исходная масса водяных паров в комнате 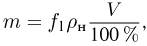 конечная масса
конечная масса 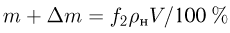 . Отсюда
. Отсюда
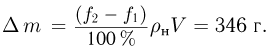
Задача №2.3.3.
Горизонтально расположенный цилиндр разделен подвижным поршнем массы 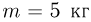 на две равные части объемом
на две равные части объемом 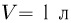 каждая. С одной стороны от поршня находится насыщенный водяной пар при температуре
каждая. С одной стороны от поршня находится насыщенный водяной пар при температуре 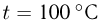 , с другой — воздух при той же температуре. Цилиндр поставили вертикально так, что снизу оказался пар. На какое расстояние х опустится поршень, если температуру в обеих частях цилиндра поддерживают неизменной? Площадь основания цилиндра
, с другой — воздух при той же температуре. Цилиндр поставили вертикально так, что снизу оказался пар. На какое расстояние х опустится поршень, если температуру в обеих частях цилиндра поддерживают неизменной? Площадь основания цилиндра 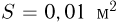 , давление насыщенного пара при температуре
, давление насыщенного пара при температуре 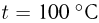 равно
равно 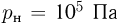 . Ускорение свободного падения принять
. Ускорение свободного падения принять 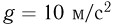 .
.
Решение:
Когда цилиндр расположен горизонтально, давление воздуха равно давлению насыщенного водяного пара 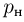 . Записывая уравнение состояния воздуха, имеем
. Записывая уравнение состояния воздуха, имеем
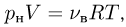
откуда количество молей воздуха 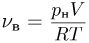 . Когда цилиндр поставили
. Когда цилиндр поставили
IX I
вертикально, давление водяного пара осталось прежним, а давление воздуха, как это следует из уравнения равновесия поршня, стало равным 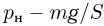 . При перемещении поршня на расстояние
. При перемещении поршня на расстояние  объем воздуха увеличился на
объем воздуха увеличился на  и уравнение состояния воздуха приняло вид:
и уравнение состояния воздуха приняло вид:
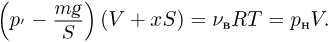
Из последнего соотношения легко найти величину  :
:
Анализ этого выражения показывает, что оно теряет смысл при  . Действительно, максимально возможное перемещение поршня (когда он опустится до дна сосуда, и весь пар сконденсируется) составляет
. Действительно, максимально возможное перемещение поршня (когда он опустится до дна сосуда, и весь пар сконденсируется) составляет 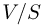 . При этом мы пренебрегаем объемом образовавшейся из пара воды, который, как показывает расчет, оказывается очень малым. В самом деле, подставляя в уравнение начального состояния пара числовые данные из условия, находим, что масса пара равна примерно 0,6 г. Следовательно, объем воды, образовавшейся при конденсации всего пара, составит около 0,06% от объема сосуда. Ответ к задаче следует сформулировать следующим образом:
. При этом мы пренебрегаем объемом образовавшейся из пара воды, который, как показывает расчет, оказывается очень малым. В самом деле, подставляя в уравнение начального состояния пара числовые данные из условия, находим, что масса пара равна примерно 0,6 г. Следовательно, объем воды, образовавшейся при конденсации всего пара, составит около 0,06% от объема сосуда. Ответ к задаче следует сформулировать следующим образом:
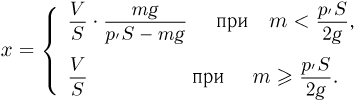
При данных из условия задачи  .
.
Задача №2.3.4.
Определить массу воды т, которую теряет человек за  = 1 час в процессе дыхания, исходя из следующих данных. Относительная влажность вдыхаемого воздуха
= 1 час в процессе дыхания, исходя из следующих данных. Относительная влажность вдыхаемого воздуха 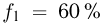 , относительная влажность выдыхаемого воздуха
, относительная влажность выдыхаемого воздуха 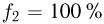 . Человек делает в среднем
. Человек делает в среднем 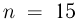 вдохов в минуту, вдыхая каждый раз
вдохов в минуту, вдыхая каждый раз 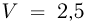 л воздуха. Температуру вдыхаемого и выдыхаемого воздуха принять
л воздуха. Температуру вдыхаемого и выдыхаемого воздуха принять 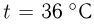 ; давление насыщенного водяного пара при этой температуре
; давление насыщенного водяного пара при этой температуре 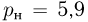 кПа. Молярная масса воды
кПа. Молярная масса воды 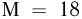 г/моль, универсальная газовая постоянная
г/моль, универсальная газовая постоянная 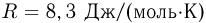 .
.
Решение:
Пусть 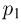 и
и 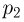 — парциальные давления водяного пара во вдыхаемом и выдыхаемом воздухе, соответственно. Для них справедливы выражения:
— парциальные давления водяного пара во вдыхаемом и выдыхаемом воздухе, соответственно. Для них справедливы выражения:
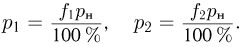
Обозначим через 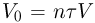 полный объем воздуха, вдыхаемого или выдыхаемого за время
полный объем воздуха, вдыхаемого или выдыхаемого за время 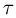 . Из уравнения Клапейрона-Менделеева, записанного для водяного пара, следует, что массы пара, содержащегося во всем объеме воздуха, который человек вдыхает и выдыхает за время
. Из уравнения Клапейрона-Менделеева, записанного для водяного пара, следует, что массы пара, содержащегося во всем объеме воздуха, который человек вдыхает и выдыхает за время 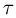 , соответственно равны:
, соответственно равны:
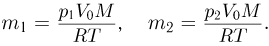
Масса теряемой человеком воды 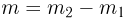 . Объединяя записанные выражения, получаем ответ:
. Объединяя записанные выражения, получаем ответ: 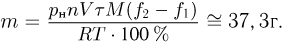
Задача №2.3.5.
В цилиндрическом сосуде под поршнем при температуре 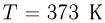 находится насыщенный водяной пар. При изотермическом сжатии пара выделилось количество тепла
находится насыщенный водяной пар. При изотермическом сжатии пара выделилось количество тепла 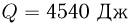 . Найти совершенную при сжатии работу
. Найти совершенную при сжатии работу 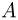 . Молярная масса воды
. Молярная масса воды 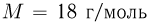 , удельная теплота парообразования воды
, удельная теплота парообразования воды 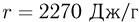 , универсальная газовая постоянная
, универсальная газовая постоянная 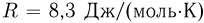 .
.
Решение:
При изотермическом сжатии пара часть его массой 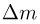 превращается в воду, за счет чего выделяется количество тепла
превращается в воду, за счет чего выделяется количество тепла 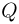 =
= 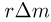 . Работа изобарного сжатия
. Работа изобарного сжатия 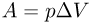 . Из уравнения состояния пара имеем:
. Из уравнения состояния пара имеем:
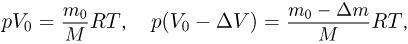
где 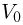 — начальный объем,
— начальный объем, 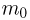 — начальная масса пара. Отсюда
— начальная масса пара. Отсюда
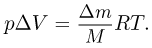
Объединяя записанные выражения, получаем ответ: 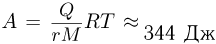 .
.
Задача №2.3.6.
В цилиндрическом сосуде под поршнем находится 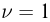 моль водяного пара при давлении
моль водяного пара при давлении 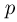 . Давление насыщенного водяного пара при этой температуре равно
. Давление насыщенного водяного пара при этой температуре равно 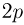 . Поршень вдвигают в цилиндр так, что объем под поршнем уменьшается в 4 раза при неизменной температуре. Найти массу
. Поршень вдвигают в цилиндр так, что объем под поршнем уменьшается в 4 раза при неизменной температуре. Найти массу 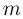 образовавшейся при этом воды. Молярная масса воды
образовавшейся при этом воды. Молярная масса воды 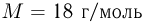 .
.
Решение:
При уменьшении объема пара в 2 раза его давление увеличивается от 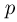 до
до 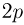 и пар становится насыщенным. Дальнейшее уменьшение объема происходит при постоянном давлении
и пар становится насыщенным. Дальнейшее уменьшение объема происходит при постоянном давлении 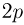 и часть пара конденсируется. Поскольку в процессе конденсации объем уменьшается в 2 раза, масса образовавшейся воды равна половине начальной массы пара. Ответ:
и часть пара конденсируется. Поскольку в процессе конденсации объем уменьшается в 2 раза, масса образовавшейся воды равна половине начальной массы пара. Ответ: 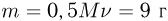 .
.
Задача №2.3.7.
Стакан объемом 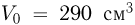 перевернули вверх дном и медленно погрузили в воду на глубину
перевернули вверх дном и медленно погрузили в воду на глубину 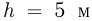 . При этом объем воздуха в стакане оказался равным
. При этом объем воздуха в стакане оказался равным 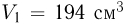 . Найти парциальное давление водяного пара, находящегося в стакане, считая его насыщенным. Относительная влажность атмосферного воздуха
. Найти парциальное давление водяного пара, находящегося в стакане, считая его насыщенным. Относительная влажность атмосферного воздуха 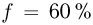 , атмосферное давление
, атмосферное давление 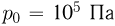 , плотность воды
, плотность воды 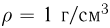 , ускорение свободного падения
, ускорение свободного падения 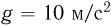 . Температуру воздуха в стакане считать постоянной. Размером стакана по сравнению с глубиной его погружения пренебречь.
. Температуру воздуха в стакане считать постоянной. Размером стакана по сравнению с глубиной его погружения пренебречь.
Решение:
До погружения в воду в стакане находилась смесь воздуха и водяного пара, причем давление этой смеси 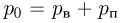 , где
, где
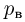 — парциальное давление воздуха,
— парциальное давление воздуха, 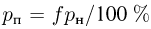 — парциальное давление пара. Отсюда
— парциальное давление пара. Отсюда 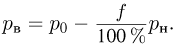
После медленного погружения стакана в воду пар в стакане достиг насыщения и давление газовой смеси в стакане стало равным 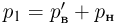 , где
, где 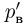 — парциальное давление воздуха,
— парциальное давление воздуха, 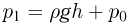 — давление воды на глубине
— давление воды на глубине 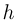 . Для парциального давления воздуха справедливо уравнение
. Для парциального давления воздуха справедливо уравнение
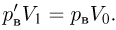
Объединяя записанные выражения, находим давление насыщенного водяного пара. Ответ:
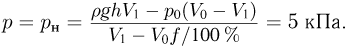
Задача №2.3.8.
В стеклянную банку объемом 1 л налили 0,5 л воды при температуре 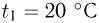 и герметично закрыли завинчивающейся крышкой. Затем банку нагрели до температуры
и герметично закрыли завинчивающейся крышкой. Затем банку нагрели до температуры 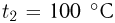 . Найти силу взаимодействия
. Найти силу взаимодействия 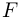 между банкой и крышкой при достижении этой температуры. Площадь крышки
между банкой и крышкой при достижении этой температуры. Площадь крышки 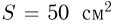 , атмосферное давление
, атмосферное давление 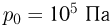 . Влажностью атмосферного воздуха, а также массой крышки пренебречь.
. Влажностью атмосферного воздуха, а также массой крышки пренебречь.
Решение:
В банке под крышкой находится воздух и насыщенный водяной пар. При температуре 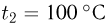 давление насыщенного пара равно атмосферному давлению:
давление насыщенного пара равно атмосферному давлению: 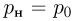 . Таким образом, парциальное давление водяного пара компенсирует атмосферное давление. Следовательно, сила, которая действует на крышку со стороны банки, равна по величине
. Таким образом, парциальное давление водяного пара компенсирует атмосферное давление. Следовательно, сила, которая действует на крышку со стороны банки, равна по величине 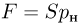 , где
, где  — парциальное давление воздуха в банке. Пренебрегая изменением объема воздуха, связанным с частичным испарением воды и ее тепловым расширением, для определения давления воздуха можно использовать закон Шарля, согласно которому
— парциальное давление воздуха в банке. Пренебрегая изменением объема воздуха, связанным с частичным испарением воды и ее тепловым расширением, для определения давления воздуха можно использовать закон Шарля, согласно которому
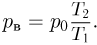
Ответ: 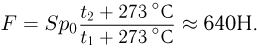
Задача №2.3.9.
В стеклянной банке объемом 1 л, закрытой завинчивающейся крышкой, находятся при температуре 100 °C 0,5 л воды и насыщенный водяной пар. Какой момент силы М нужно приложить к крышке, чтобы отвернуть ее после того, как банка остынет до температуры 20 °C? Давление насыщенного водяного пара при температуре 20 °C составляет 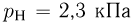 . Атмосферное давление
. Атмосферное давление 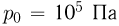 . Радиус крышки
. Радиус крышки 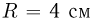 , коэффициент трения между плоскостью крышки и верхней частью банки
, коэффициент трения между плоскостью крышки и верхней частью банки 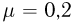 . Массой крышки и трением в резьбовом соединении крышки с банкой пренебречь.
. Массой крышки и трением в резьбовом соединении крышки с банкой пренебречь.
Решение:
После остывания банки в ней будет находиться вода и насыщенный пар при давлении 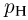 . Следовательно, сила, с которой крышка будет давить на банку,
. Следовательно, сила, с которой крышка будет давить на банку, 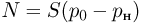 , где
, где 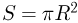 — площадь крышки. Сила трения между крышкой и банкой
— площадь крышки. Сила трения между крышкой и банкой 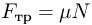 , момент этой силы
, момент этой силы 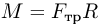 . Объединяя записанные выражения, получаем ответ:
. Объединяя записанные выражения, получаем ответ:
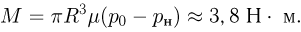
Задача №2.3.10.
В калориметре находилось  г воды при температуре
г воды при температуре 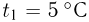 . К ней долили еще
. К ней долили еще  г воды при температуре
г воды при температуре 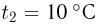 и положили
и положили  г льда при температуре
г льда при температуре 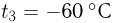 . Какая масса
. Какая масса  льда оказалась в калориметре после установления теплового равновесия? Удельные теплоемкости воды и льда, соответственно,
льда оказалась в калориметре после установления теплового равновесия? Удельные теплоемкости воды и льда, соответственно, 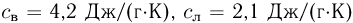 , удельная теплота плавления льда
, удельная теплота плавления льда 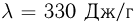 . Теплоемкостью калориметра пренебречь.
. Теплоемкостью калориметра пренебречь.
Решение:
Решение задач такого типа необходимо начинать с числовых оценок количеств тепла, которыми обмениваются различные компоненты системы при установлении теплового равновесия. Определим вначале количество тепла, которое может отдать вода при остывании до температуры плавления льда (0°С):
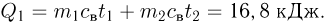
Количество тепла, требующееся для нагревания льда до температуры плавления, равно
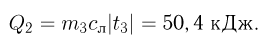
Сравнивая эти величины, видим, что тепла, отдаваемого водой при остывании, недостаточно для нагревания льда до 0°С. В то же время, количество тепла, которое может отдать вся вода при замерзании,
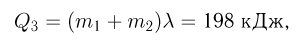
явно превышает количество тепла, требующееся для нагревания льда до температуры плавления. Следовательно, при установлении теплового равновесия в калориметре вода остынет до 0°С, часть ее замерзнет и весь лед будет иметь температуру плавления. Обозначив через 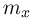 массу замерзшей воды, запишем уравнение теплового баланса:
массу замерзшей воды, запишем уравнение теплового баланса:
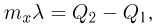 откуда
откуда 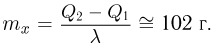
Таким образом, после установления теплового равновесия в калориметре образуется смесь воды и льда при нулевой температуре, причем масса льда 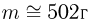 .
.
Задача №2.3.11.
В цилиндрическом сосуде с площадью основания S = 11  находится кубик льда массой
находится кубик льда массой 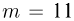 г при температуре
г при температуре 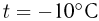 . Какое минимальное количество теплоты
. Какое минимальное количество теплоты  нужно сообщить льду для того, чтобы при дальнейшем нагревании уровень воды в сосуде не изменялся? Удельная теплоемкость льда
нужно сообщить льду для того, чтобы при дальнейшем нагревании уровень воды в сосуде не изменялся? Удельная теплоемкость льда 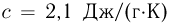 , удельная теплота плавления льда
, удельная теплота плавления льда  , плотность льда
, плотность льда 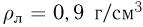 . При расчете принять, что при плавлении кусок льда сохраняет форму куба.
. При расчете принять, что при плавлении кусок льда сохраняет форму куба.
Решение:
Уровень воды в сосуде будет подниматься до момента всплытия льда. После этого, пока весь лед не растает, уровень воды будет находиться на одной и той же высоте 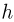 , которая определяется объемом воды, образовавшейся из всего растаявшего льда:
, которая определяется объемом воды, образовавшейся из всего растаявшего льда:
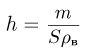
Здесь 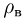 — плотность воды. С другой стороны, лед всплывет, когда глубина подводной части кубика станет равной
— плотность воды. С другой стороны, лед всплывет, когда глубина подводной части кубика станет равной 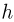 . Из условия плавания частично растаявшего кубика
. Из условия плавания частично растаявшего кубика
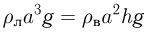
находим длину его ребра: 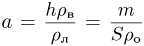 . Отсюда масса начавшего плавать кубика
. Отсюда масса начавшего плавать кубика
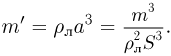
Таким образом, для того, чтобы кубик всплыл, нужно, чтобы растаяла масса льда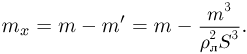
Для этого требуется количество тепла
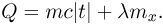
Объединяя записанные выражения, получаем ответ:
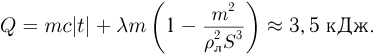
Задача №2.3.12.
В чайник налили воды при температуре 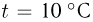 и поставили на электроплитку. Через время
и поставили на электроплитку. Через время 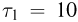 мин вода закипела. Через какое время
мин вода закипела. Через какое время 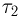 вода полностью выкипит? Удельная теплоемкость воды
вода полностью выкипит? Удельная теплоемкость воды 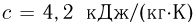 , удельная теплота парообразования
, удельная теплота парообразования 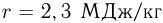 . Температура кипения воды
. Температура кипения воды 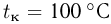 . Теплоемкостью чайника пренебречь.
. Теплоемкостью чайника пренебречь.
Решение:
Обозначив через  начальную массу воды в чайнике, найдем количества тепла
начальную массу воды в чайнике, найдем количества тепла 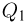 и
и 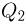 требующиеся, соответственно, для нагревания воды до температуры кипения и для превращения ее в пар:
требующиеся, соответственно, для нагревания воды до температуры кипения и для превращения ее в пар:
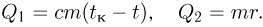
Пусть 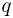 — мощность плитки; тогда
— мощность плитки; тогда
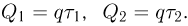
Объединяя эти выражения, получаем ответ:
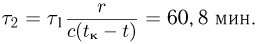
Задача №2.3.13.
В теплоизолированном сосуде в начальный момент находится одноатомный газ при температуре 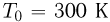 и кусочек железа массы
и кусочек железа массы 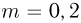 кг, нагретый до температуры
кг, нагретый до температуры 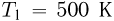 . Начальное давление газа
. Начальное давление газа 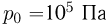 , его объем
, его объем 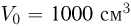 , удельная теплоемкость железа
, удельная теплоемкость железа 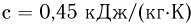 . Найти давление газа в равновесном состоянии, считая объем газа неизменным.
. Найти давление газа в равновесном состоянии, считая объем газа неизменным.
Решение:
Из уравнения теплового баланса имеем:
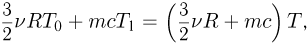
где 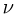 — число молей газа,
— число молей газа, 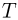 — установившаяся (равновесная) температура в сосуде. Число молей газа может быть легко найдено из уравнения его начального состояния:
— установившаяся (равновесная) температура в сосуде. Число молей газа может быть легко найдено из уравнения его начального состояния: 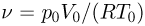 . Подставляя
. Подставляя  в первое соотношение, находим установившуюся температуру:
в первое соотношение, находим установившуюся температуру:
Поскольку объем газа постоянен, его давление в конечном состоянии 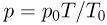 . Объединяя записанные выражения, получаем ответ:
. Объединяя записанные выражения, получаем ответ: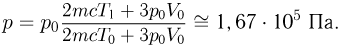
Поверхностное натяжение в жидкостях. Определения, понятия и законы
Сила поверхностного натяжения
Многочисленные наблюдения и опыты показывают, что любая жидкость стремится принять такую форму, при которой ее свободная поверхность имеет наименьшую площадь. С точки зрения молекулярно-кинетической теории причина этого явления заключается в наличии сил притяжения между молекулами жидкости, а также подвижностью молекул, т.е. возможностью свободного перемещения молекул жидкости друг относительно друга.
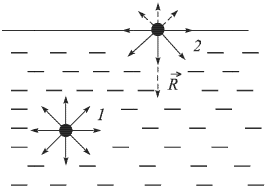
Равнодействующая  сил, действующая на молекулу в поверхностном слое.
сил, действующая на молекулу в поверхностном слое.
Внутри жидкости силы притяжения, действующие на отдельную молекулу 1 со стороны соседних с ней молекул, взаимно компенсируются (рис. 2.4.1). Любая молекула 2, находящаяся у свободной поверхности жидкости, испытывает меньшее притяжение вверх со стороны молекул пара и большее притяжение вниз со стороны молекул жидкости. В результате равнодействующая 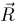 сил, действующих на любую молекулу, расположенную в поверхностном слое, направлена вниз. Под действием этих сил молекулы стремятся переместиться с поверхности вглубь жидкости. Число молекул, находящихся на поверхности, уменьшается до тех пор, пока площадь свободной поверхности жидкости не достигнет минимально возможного в данных условиях значения.
сил, действующих на любую молекулу, расположенную в поверхностном слое, направлена вниз. Под действием этих сил молекулы стремятся переместиться с поверхности вглубь жидкости. Число молекул, находящихся на поверхности, уменьшается до тех пор, пока площадь свободной поверхности жидкости не достигнет минимально возможного в данных условиях значения.
Молекулы поверхностного слоя находятся в среднем на больших расстояниях друг от друга, чем молекулы внутри жидкости. Жидкость в поверхностном слое находится в растянутом состоянии. Свойство сокращения свободной поверхности жидкости во многих явлениях выглядит таким образом, как будто жидкость покрыта растянутой эластичной пленкой, стремящейся к сокращению. Однако происхождение поверхностных сил иное, чем упругих сил растянутой эластичной пленки. При сокращении поверхности эластичной пленки силы упругости ослабевают, т. к. среднее расстояние между молекулами уменьшается. Напротив, силы поверхностного натяжения при сокращении свободной поверхности жидкости не изменяются, т. к. плотность жидкости, а следовательно, и среднее расстояние между молекулами на поверхности остаются постоянными.
Для перенесения молекулы из глубины объема жидкости в ее поверхностный слой необходимо совершить работу по преодолению силы 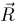 , показанной на рис. 2.4.1. Эта работа идет на увеличение поверхностной энергии, т. е. избыточной потенциальной энергии, которой обладают молекулы в поверхностном слое по сравнению с их потенциальной энергией внутри объема жидкости.
, показанной на рис. 2.4.1. Эта работа идет на увеличение поверхностной энергии, т. е. избыточной потенциальной энергии, которой обладают молекулы в поверхностном слое по сравнению с их потенциальной энергией внутри объема жидкости.
Поверхностная энергия прямо пропорциональна площади поверхности жидкости. Поэтому отношение поверхностной энергии 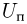 участка поверхности жидкости к площади
участка поверхности жидкости к площади 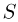 этого участка есть величина постоянная, не зависящая от площади
этого участка есть величина постоянная, не зависящая от площади 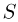 . Эту величину называют коэффициентом поверхностного натяжения или просто поверхностным натяжением
. Эту величину называют коэффициентом поверхностного натяжения или просто поверхностным натяжением 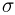 :
:
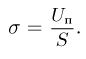
Поверхностное натяжение представляет собой удельную поверхностную энергию, т. е. энергию, приходящуюся на поверхность единичной площади. С термодинамической точки зрения поверхностная энергия — это один из видов внутренней энергии.
В СИ поверхностное натяжение измеряется в джоулях на квадратный метр ( ). Так как
). Так как  , то поверхностное натяжение можно также выражать в ньютонах на метр (Н/м).
, то поверхностное натяжение можно также выражать в ньютонах на метр (Н/м).
Силой поверхностного натяжения называют силу, которая действует вдоль поверхности жидкости перпендикулярно к линии, ограничивающей эту поверхность, и стремится сократить ее до минимума.
Для того, чтобы лучше понять, как проявляет себя сила поверхностного натяжения, рассмотрим следующий опыт (рис. 2.4.2). Возьмем прямоугольную проволочную рамку, одна из сторон которой (ЛВ) длиной 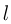 может без трения перемещаться в вертикальной плоскости. Погрузив рамку в мыльный раствор, получим на ней мыльную пленку. Как только мы вытащим рамку из мыльного раствора, проволока АВ придет в движение и мыльная пленка будет сокращать свою поверхность. Следовательно, на проволоку АВ действует сила поверхностного натяжения, направленная перпендикулярно проволоке в сторону мыльной пленки.
может без трения перемещаться в вертикальной плоскости. Погрузив рамку в мыльный раствор, получим на ней мыльную пленку. Как только мы вытащим рамку из мыльного раствора, проволока АВ придет в движение и мыльная пленка будет сокращать свою поверхность. Следовательно, на проволоку АВ действует сила поверхностного натяжения, направленная перпендикулярно проволоке в сторону мыльной пленки.
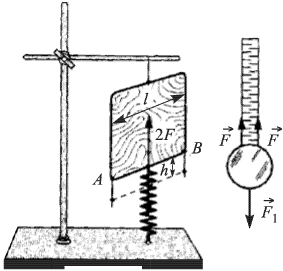
Чтобы измерить силу поверхностного натяжения, прикрепим к проволоке АВ мягкую пружину, закрепленную на основании штатива (рис. 2.4.2). Сила упругости пружины вместе с силой тяжести, действующей на проволоку АВ, в сумме составляют результирующую силу 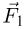 . Проволока будет находиться в равновесии, если
. Проволока будет находиться в равновесии, если 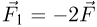 , где
, где  — сила поверхностного натяжения, действующая на подвижную проволоку со стороны одной из поверхностей пленки. Отсюда
— сила поверхностного натяжения, действующая на подвижную проволоку со стороны одной из поверхностей пленки. Отсюда  .
.
Приравнивая работу силы  изменению поверхностной энергии пленки, нетрудно получить следующее выражение для силы поверхностного натяжения:
изменению поверхностной энергии пленки, нетрудно получить следующее выражение для силы поверхностного натяжения:
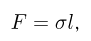
где  — длина границы поверхностного слоя.
— длина границы поверхностного слоя.
Явления смачивания и несмачивания. На границе жидкость — твердое тело необходимо учитывать силы притяжения между молекулами жидкости и молекулами твердого тела. Если силы притяжения между молекулами жидкости и твердого тела больше, чем силы притяжения между молекулами самой жидкости, то говорят, что жидкость смачивает твердое тело. Если силы притяжения между молекулами жидкости больше сил притяжения молекул твердого тела и молекул жидкости, то жидкость не смачивает твердое тело.
Характеристикой поведения жидкости на поверхности твердого тела служит краевой угол т.е. угол $, образованный касательной к поверхности жидкости и поверхностью твердого тела, отсчитываемый внутрь жидкости. Если жидкость смачивает твердое тело, то она растекается по его поверхности и краевой угол  является острым (рис. 2.4.3, а). Несмачивающая жидкость на поверхности твердого тела стягивается в каплю и краевой угол
является острым (рис. 2.4.3, а). Несмачивающая жидкость на поверхности твердого тела стягивается в каплю и краевой угол  тупой (рис. 2.4.3, б). В случае полного смачивания
тупой (рис. 2.4.3, б). В случае полного смачивания 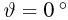 , а в случае полного несмачивания
, а в случае полного несмачивания 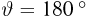 .
.

Взаимодействие молекул жидкости с молекулами твердого тела влияет и на форму поверхности жидкости, налитой в сосуд. Если большое количество жидкости налито в широкий сосуд, то форма ее поверхности определяется силой тяжести, которая обеспечивает плоскую и горизонтальную поверхность. Однако у самых стенок сосуда поверхность жидкости искривлена, т. е. образуется мениск, вогнутый у смачивающих жидкостей (рис. 2.4.4, а) и выпуклый у несмачивающих (рис. 2.4.4, б). Если сближать противоположные стенки (брать более узкий сосуд), то горизонтальная часть свободной поверхности жидкости будет сокращаться, пока не исчезнет совсем. В узких трубках при полном смачивании (или несмачивании) мениск представляет собой полусферу, радиус которой равен радиусу канала трубки.
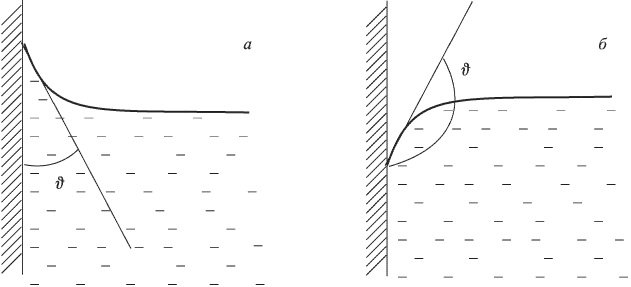
Давление под искривленной поверхностью жидкости
Если поверхность жидкости искривлена, то в зависимости от знака кривизны поверхности давление внутри жидкости может быть как больше, так и меньше внешнего давления.
Пусть 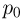 — внешнее давление над поверхностью жидкости (например, атмосферное давление). Если поверхность жидкости плоская (рис. 2.4.5, а), то непосредственно под ней давление в жидкости равно внешнему:
— внешнее давление над поверхностью жидкости (например, атмосферное давление). Если поверхность жидкости плоская (рис. 2.4.5, а), то непосредственно под ней давление в жидкости равно внешнему:
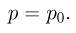
Будем считать, что искривленная поверхность жидкости имеет форму части сферы радиусом 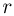 . Давление под выпуклой поверхностью (рис. 2.4.5, б) больше внешнего и равно
. Давление под выпуклой поверхностью (рис. 2.4.5, б) больше внешнего и равно
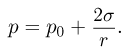
Давление под вогнутой поверхностью (рис. 2.4.6, в) меньше внешнего и равно
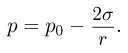
Капиллярные явления
Особенности взаимодействия жидкостей со смачиваемыми и несмачиваемыми поверхностями твердых тел являются причиной капиллярных явлений. Под капиллярными явлениями понимают подъем или опускание жидкости в тонких трубках — капиллярах — по сравнению с уровнем жидкости в широких сосудах.
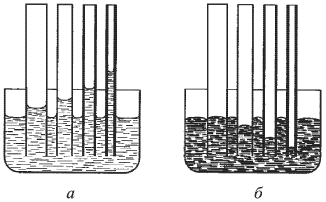
Смачивающая жидкость (например, вода в стеклянной трубке) поднимается по капилляру. При этом, чем меньше радиус трубки, тем на большую высоту поднимается в ней жидкость (рис. 2.4.6, а). Жидкость, не смачивающая стен-ки капилляра (например, ртуть в стеклянной трубке), опускается ниже уровня жидкости в широком сосуде (рис. 2.4.6, б.)
При полном смачивании жидкостью внутренней поверхности трубки сила поверхностного натяжения направлена вдоль поверхности трубки и перпендикулярно границе соприкосновения жидкости со стенкой трубки. Подъем жидкости вдоль смачиваемой поверхности продолжается до тех пор, пока сила тяжести, действующая на столб жидкости в капилляре, не станет равной по величине силе поверхностного натяжения. Из условия равновесия столбика жидкости легко найти, что высота подъема жидкости в капилляре равна
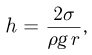
где  — плотность жидкости,
— плотность жидкости, 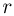 — внутренний радиус капилляра,
— внутренний радиус капилляра, 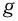 — ускорение свободного падения.
— ускорение свободного падения.
Глубина 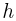 , на которую опускается в капилляре несмачивающая жидкость, также вычисляется по формуле (2.4.6).
, на которую опускается в капилляре несмачивающая жидкость, также вычисляется по формуле (2.4.6).
Примеры решения задач №4:
Задача №2.4.1.
Какова масса 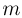 капли воды, вытекающей из стеклянной трубки диаметром
капли воды, вытекающей из стеклянной трубки диаметром 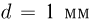 , если считать, что диаметр шейки капли в момент отрыва равен внутреннему диаметру трубки (см. рисунок)? Поверхностное натяжение воды
, если считать, что диаметр шейки капли в момент отрыва равен внутреннему диаметру трубки (см. рисунок)? Поверхностное натяжение воды 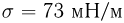 . Ускорение свободного падения принять
. Ускорение свободного падения принять 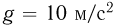 .
.
Решение:
Процесс образования капли, вытекающей из трубки, схематично изображен на рисунке а. Перед отрывом капли образуется шейка, диаметр которой, вообще говоря, несколько меньше внутреннего диаметра трубки. Сила поверхностного натяжения воды, действующая перпендикулярно окружности этой шейки (рисунок б, удерживает каплю от падения. Отрыв капли происходит при выполнении условия
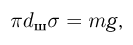
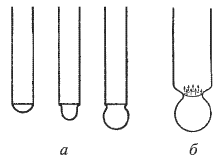
где 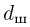 — диаметр шейки. Полагая приближенно, что диаметр шейки равен внутреннему диаметру трубки, получаем ответ:
— диаметр шейки. Полагая приближенно, что диаметр шейки равен внутреннему диаметру трубки, получаем ответ:
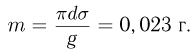
Задача №2.4.2.
Для изготовления ртутного барометра взяли стеклянную трубку диаметром 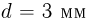 . Какую поправку
. Какую поправку  нужно вносить в показания барометра, если учесть поверхностное натяжение ртути? Ртуть не смачивает стекло. Поверхностное натяжение ртути
нужно вносить в показания барометра, если учесть поверхностное натяжение ртути? Ртуть не смачивает стекло. Поверхностное натяжение ртути 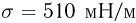 , плотность ртути
, плотность ртути 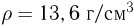 . Ускорение свободного падения принять
. Ускорение свободного падения принять 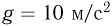 .
.
Решение:
В отсутствие капиллярных эффектов равновесие ртути в трубке достигается при выполнении равенства
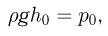
где 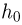 — высота столба ртути,
— высота столба ртути, 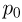 — атмосферное давление. Поскольку ртуть не смачивает стекло, поверхность ртути в трубке образует выпуклый мениск. Полагая, что радиус мениска
— атмосферное давление. Поскольку ртуть не смачивает стекло, поверхность ртути в трубке образует выпуклый мениск. Полагая, что радиус мениска 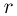 совпадает с радиусом трубки, находим, что давление ртути в трубке непосредственно под искривленной поверхностью равно
совпадает с радиусом трубки, находим, что давление ртути в трубке непосредственно под искривленной поверхностью равно 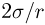 . Следовательно, с учетом капиллярных явлений условие равновесия ртути принимает вид:
. Следовательно, с учетом капиллярных явлений условие равновесия ртути принимает вид:
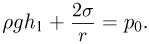
Влияние поверхностного натяжения ртути сводится к тому, что высота столба ртути в трубке при неизменном атмосферном давлении уменьшается на величину  Поэтому для правильного измерения атмосферного давления нужно прибавлять к показаниям барометра
Поэтому для правильного измерения атмосферного давления нужно прибавлять к показаниям барометра 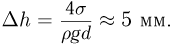
Задача №2.4.3.
В дне чайника имеется круглое отверстие диаметром d = 1 мм. До какой высоты 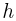 можно налить воду в чайник, чтобы она не выливалась через отверстие? Поверхностное натяжение воды
можно налить воду в чайник, чтобы она не выливалась через отверстие? Поверхностное натяжение воды 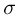 = 73 мН/м, плотность воды
= 73 мН/м, плотность воды 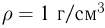 . Ускорение свободного падения принять
. Ускорение свободного падения принять 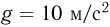 .
.
Решение:
Выделим мысленно вертикальный столбик воды сечением 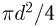 , расположенный над отверстием. Этот столбик ограничен снизу сферической поверхностью воды, образующей мениск радиусом
, расположенный над отверстием. Этот столбик ограничен снизу сферической поверхностью воды, образующей мениск радиусом 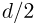 . Избыточное давление, создаваемое искривленной поверхностью воды в нижней точке рассматриваемого столбика, равно
. Избыточное давление, создаваемое искривленной поверхностью воды в нижней точке рассматриваемого столбика, равно 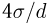 . Столбик находится в равновесии, если выполнено условие
. Столбик находится в равновесии, если выполнено условие
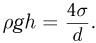
Отсюда легко найти ответ: 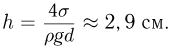
Задача №2.4.4.
На какую величину  давление воздуха внутри мыльного пузыря больше атмосферного давления, если диаметр пузыря
давление воздуха внутри мыльного пузыря больше атмосферного давления, если диаметр пузыря  ? Какую работу
? Какую работу 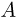 нужно совершить, чтобы выдуть такой пузырь? Поверхностное натяжение мыльного раствора
нужно совершить, чтобы выдуть такой пузырь? Поверхностное натяжение мыльного раствора 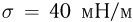 . Толщину мыльной пленки, образующей пузырь, считать пренебрежимо малой.
. Толщину мыльной пленки, образующей пузырь, считать пренебрежимо малой.
Решение:
Мыльная пленка образует две поверхности: внешнюю и внутреннюю. Сечение пленки изображено на рисунке, где через  обозначена ее толщина. Давления в толще пленки и внутри пузыря определяются формулами:
обозначена ее толщина. Давления в толще пленки и внутри пузыря определяются формулами:
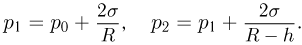
Пренебрегая толщиной пленки, получаем для разности давлений внутри и снаружи пузыря следующее выражение: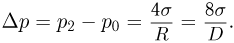
Таким образом, избыточное давление внутри пузыря создается двумя поверхностями мыльной пленки. Работа по выдуванию пузыря равна изменению поверхностной энергии пленки 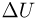 . Считая, что площадь сечения трубки, из которой выдувают пузырь, мала, находим:
. Считая, что площадь сечения трубки, из которой выдувают пузырь, мала, находим:
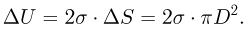
Ответ: 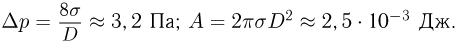
Тепловое расширение твердых тел и жидкостей. Определения, понятия и законы
Тепловым расширением называется увеличение линейных размеров и объемов тел, происходящее при повышении их температуры. Причину этого явления можно объяснить, анализируя зависимость потенциальной энергии взаимодействия молекул 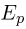 от расстояния
от расстояния 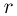 между ними (рис. 2.5.1). Как видно из рисунка, кривая потенциальной энергии несимметрична относительно точки
между ними (рис. 2.5.1). Как видно из рисунка, кривая потенциальной энергии несимметрична относительно точки 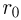 , в которой потенциальная энергия минимальна. В точке
, в которой потенциальная энергия минимальна. В точке  силы взаимодействия между
силы взаимодействия между
молекулами обращаются в нуль. При 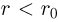 между молекулами возникают силы отталкивания, и потенциальная энергия очень быстро нарастает с уменьшением
между молекулами возникают силы отталкивания, и потенциальная энергия очень быстро нарастает с уменьшением  . При
. При 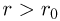 между молекулами действуют силы притяжения, и потенциальная энергия сравнительно медленно растет с увеличением
между молекулами действуют силы притяжения, и потенциальная энергия сравнительно медленно растет с увеличением 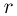 .
.
Рассмотрим движение какой-либо молекулы в силовом поле другой молекулы, которую примем за неподвижную. В зависимости от величины полной энергии движущейся молекулы 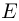 она совершает колебания с различной амплитудой. Так, при энергии
она совершает колебания с различной амплитудой. Так, при энергии 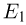 молекула колеблется между точками
молекула колеблется между точками 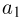 и
и 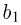 , при энергии
, при энергии 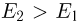 — между точками
— между точками 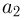 и
и 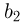 , при энергии
, при энергии 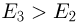 — между точками
— между точками 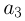 и
и 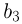 и т. д. (см. рис. 2.5.1), причем положение равновесия при каждом значении энергии
и т. д. (см. рис. 2.5.1), причем положение равновесия при каждом значении энергии 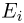 , находится примерно посередине между соответствующими точками
, находится примерно посередине между соответствующими точками 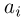 , и
, и 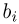 . Из рисунка видно, что с ростом энергии молекулы положение равновесия смещается в сторону больших значений
. Из рисунка видно, что с ростом энергии молекулы положение равновесия смещается в сторону больших значений 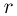 . Поскольку энергия теплового движения пропорциональна температуре, отсюда следует, что при нагревании тела средние расстояния между молекулами возрастают и размеры тела увеличиваются. Важно отметить, что если бы кривая потенциальной энергии была симметричной, то среднее положение молекулы при любой энергии соответствовало бы расстоянию
. Поскольку энергия теплового движения пропорциональна температуре, отсюда следует, что при нагревании тела средние расстояния между молекулами возрастают и размеры тела увеличиваются. Важно отметить, что если бы кривая потенциальной энергии была симметричной, то среднее положение молекулы при любой энергии соответствовало бы расстоянию 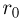 . В этом случае не менялись бы средние расстояния между молекулами при нагревании, т. е. не наблюдалось бы тепловое расширение.
. В этом случае не менялись бы средние расстояния между молекулами при нагревании, т. е. не наблюдалось бы тепловое расширение.
Тепловое линейное расширение
Опыт показывает, что в некотором температурном диапазоне изменение линейных размеров твердых тел прямо пропорционально изменению температуры. Для количественного описания теплового линейного расширения удобно использовать относительное удлинение тела, т. е. отношение абсолютного удлинения 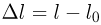 к первоначальной длине
к первоначальной длине 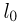 . В соответствии с законом теплового линейного расширения относительное удлинение тела
. В соответствии с законом теплового линейного расширения относительное удлинение тела 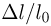 пропорционально изменению температуры
пропорционально изменению температуры 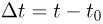 :
:
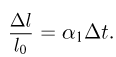
Коэффициент пропорциональности  называют температурным коэффициентом линейного расширения. Этот коэффициент показывает, на какую долю своего первоначального значения изменяются линейные размеры тела при его нагревании на 1 К. Коэффициент линейного расширения зависит от вещества, из которого состоит тело, а также от температуры. Если температура меняется в небольших пределах, зависимостью
называют температурным коэффициентом линейного расширения. Этот коэффициент показывает, на какую долю своего первоначального значения изменяются линейные размеры тела при его нагревании на 1 К. Коэффициент линейного расширения зависит от вещества, из которого состоит тело, а также от температуры. Если температура меняется в небольших пределах, зависимостью  от температуры можно пренебречь и считать температурный коэффициент линейного расширения величиной постоянной для данного вещества.
от температуры можно пренебречь и считать температурный коэффициент линейного расширения величиной постоянной для данного вещества.
Линейные размеры тела, как вытекает их формулы (2.5.1), зависят от изменения температуры следующим образом:
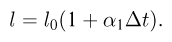
Поскольку при равномерном нагревании (или охлаждении) твердого тела все его линейные размеры меняются по одному и тому же закону, форма твердого тела с изменением температуры не меняется. Так, у круглого стержня при нагревании увеличивается диаметр, притом во столько же раз, во сколько увеличивается длина стержня. У пластинки в одно и то же число раз увеличиваются длина, ширина и толщина. Если начертить на пластинке какую-либо линию, то длина этой линии при нагревании увеличится в такое же число раз. При нагревании пластинки, имеющей, например, круглое отверстие, диаметр отверстия также увеличится, причем в такое же число раз, что и размеры пластинки. Расширение пластинки с отверстием происходит так же, как если бы она была сплошной.
Тепловое объемное расширение
Увеличение линейных размеров твердого тела при нагревании приводит к увеличению его объема. При изучении теплового объемного расширения, как и в случае линейного расширения, удобно рассматривать относительное изменение объема 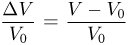 . Измерения показывают, что в пределах не очень большого интервала температур относительное изменение объема пропорционально изменению температуры
. Измерения показывают, что в пределах не очень большого интервала температур относительное изменение объема пропорционально изменению температуры 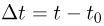 :
:
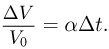
Коэффициент пропорциональности 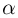 называют температурным коэффициентом объемного расширения. Этот коэффициент показывает, на какую долю своего первоначального значения изменяется объем тела при изменении температуры на 1 К. Коэффициент объемного расширения, как и коэффициент линейного расширения, зависит от вещества, из которого состоит тело, и от температуры. Зависимость
называют температурным коэффициентом объемного расширения. Этот коэффициент показывает, на какую долю своего первоначального значения изменяется объем тела при изменении температуры на 1 К. Коэффициент объемного расширения, как и коэффициент линейного расширения, зависит от вещества, из которого состоит тело, и от температуры. Зависимость 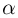 от температуры незначительно и ею можно пренебречь, если интервал изменения температуры невелик.
от температуры незначительно и ею можно пренебречь, если интервал изменения температуры невелик.
Из формулы (2.5.3) можно найти выражение для объема тела при любой температуре:
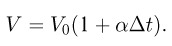
Объем полого твердого тела (сосуда) при равномерном нагревании увеличивается так, как если бы это тело было сплошным. Объем полости в сосуде при его нагревании увеличивается так, как увеличился бы объем тела, изготовленного из того же вещества, что и сосуд, и имеющего форму и размер полости.
Коэффициент линейного расширения  и коэффициент объемного расширения
и коэффициент объемного расширения 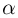 связаны между собой. Эта связь наиболее проста, если изменения температуры малы:
связаны между собой. Эта связь наиболее проста, если изменения температуры малы:
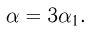
Температурный коэффициент объемного расширения равен утроенному температурному коэффициенту линейного расширения. По этой причине в справочной литературе для твердых тел приводятся только температурные коэффициенты линейного расширения.
С изменением температуры тел изменяется их плотность. Если при температуре  плотность тела равна
плотность тела равна  , то при температуре
, то при температуре 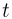 плотность тела равна
плотность тела равна
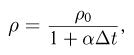
где 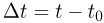 . Для приближенных расчетов в небольших температурных интервалах можно использовать для плотности также формулу
. Для приближенных расчетов в небольших температурных интервалах можно использовать для плотности также формулу
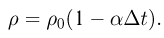
Тепловое расширение жидкостей
Поскольку жидкости всегда принимают форму сосуда, в котором они находится, для них имеет смысл только коэффициент объемного расширения. Из-за того, что связи между молекулами в жидкостях слабее, чем связи между молекулами в твердых телах, при одинаковом нагревании жидкости расширяются в большей степени, чем твердые тела. Температурный коэффициент объемного расширения большинства жидкостей на один — два порядка превышает коэффициент объемного расширения большинства твердых тел.
Изменение объема жидкости при нагревании подчиняется формулам (2.5.3), (2.5.4), для вычисления плотности жидкости при заданной температуре справедливы формулы (2.5.6), (2.5.7).
Особенности теплового расширения воды
Вода обладает особыми свойствами, отличающими ее от других жидкостей. При нагревании от О до 4 °C объем воды не увеличивается, а уменьшается. Лишь начиная с 4 °C объем воды при нагревании начинает возрастать. Таким образом, при 4 °C объем воды минимален, а плотность максимальна.
Это свойство воды оказывает большое влияние на характер теплообмена в водоемах. При понижении температуры воздуха верхние слои воды охлаждаются, их плотность понижается и они опускаются вниз. В результате такого перемешивания вода охлаждается по всей глубине водоема. Но после достижения температуры воздуха 4 °C дальнейшее охлаждение воды уже уменьшает ее плотность, и холодные слои воды остаются на поверхности. Перемешивание воды прекращается. Когда температура воздуха становится отрицательной, на поверхности воды образуется лед, который обладает весьма малой теплопроводностью.
Поэтому достаточно глубокие водоемы не промерзают до дна. Даже при сильных морозах вода вблизи дна в них имеет температуру около 4 °C.
Примеры решения задач №5:
Задача №2.5.1.
Диаметр стеклянной пробки, застрявшей в горлышке флакона, 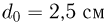 . Чтобы вынуть пробку, горлышко нагрели до температуры
. Чтобы вынуть пробку, горлышко нагрели до температуры 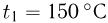 . Сама пробка успела при этом нагреться до температуры
. Сама пробка успела при этом нагреться до температуры 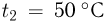 . Какой зазор
. Какой зазор 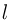 между горлышком и пробкой образовался при этом? Температурный коэффициент линейного расширения стекла
между горлышком и пробкой образовался при этом? Температурный коэффициент линейного расширения стекла 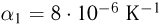 .
.
Решение:
Пусть  — начальная температура флакона и пробки. В соответствии с законом теплового линейного расширения диаметры горлышка флакона
— начальная температура флакона и пробки. В соответствии с законом теплового линейного расширения диаметры горлышка флакона  и пробки
и пробки  при нагревании станут равными:
при нагревании станут равными:
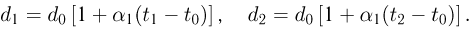
Зазор между горлышком и пробкой определяется как 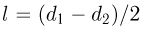 . Ответ:
. Ответ: 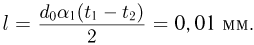
Задача №2.5.2.
Сообщающиеся сосуды заполнены жидкостью, имеющей температуру 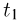 . При нагревании жидкости в одном из сосудов до температуры
. При нагревании жидкости в одном из сосудов до температуры 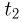 уровень жидкости в этом сосуде установился на высоте
уровень жидкости в этом сосуде установился на высоте 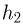 , а в другом сосуде — на высоте
, а в другом сосуде — на высоте 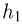 . Найти температурный коэффициент объемного расширения жидкости
. Найти температурный коэффициент объемного расширения жидкости 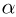 . Тепловым расширением сосудов пренебречь.
. Тепловым расширением сосудов пренебречь.
Решение:
Равновесие жидкости достигается при равенстве гидростатических давлений у дна сосудов, т.е. при выполнении условия:
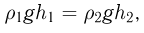
где  и
и  — плотности жидкости при температурах
— плотности жидкости при температурах  и
и 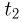 соответственно. В соответствии с законом теплового объемного расширения
соответственно. В соответствии с законом теплового объемного расширения
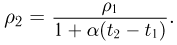
Объединяя записанные соотношения, получаем ответ: 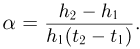
Задача №2.5.3.
Определите объем 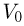 шарика ртутного термометра, если известно, что при температуре
шарика ртутного термометра, если известно, что при температуре 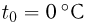 ртуть заполняет только шарик, а объем трубки термометра между делениями, соответствующими температурам
ртуть заполняет только шарик, а объем трубки термометра между делениями, соответствующими температурам 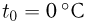 и
и 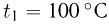 , равен
, равен 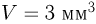 . Температурный коэффициент объемного расширения ртути
. Температурный коэффициент объемного расширения ртути 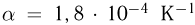 , температурный коэффициент линейного расширения стекла
, температурный коэффициент линейного расширения стекла 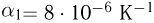 .
.
Решение:
По условию  — объем шарика термометра при температуре
— объем шарика термометра при температуре 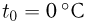 . При температуре
. При температуре 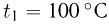 объем шарика и трубки составляет величину
объем шарика и трубки составляет величину
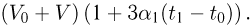
Этот объем равен объему ртути
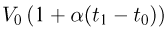
при той же температуре. Из равенства
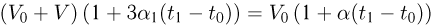 получаем ответ:
получаем ответ: 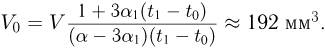
Возможно эти дополнительные страницы вам будут полезны:
- Предмет физика
- Готовые задачи по физике
- Решение задач по физической механике
- Заказать работу по физике
- Помощь по физике
- Решение задач по электростатике и электродинамике
- Постоянный ток задачи с решением
- Магнетизм задачи с решением
- Электромагнитные колебания задачи с решением
- Задачи по оптике с решением
- Атом и атомное ядро решение задач

