Оглавление:
Более сложны задачи на смеси, процентное содержание и концентрации. Смесь или сплав состоит из нескольких веществ (компонентов). Отношение объема (веса, массы) одного из компонентов ко всему объему (весу, массе) смеси называется концентрацией этого компонента. О какой концентрации (объемной, весовой, массовой) идет речь в конкретной задаче, всегда ясно из ее условия. Концентрации — это безразмерные величины, выражающиеся либо в долях, либо в процентах. Очевидно, что сумма концентраций всех веществ, составляющих смесь, равна 1, если концентрации измеряются в долях, и равна 100%, если концентрации измеряются в процентах.
Задача №4
Смешали 30%-й раствор соляной кислоты с 10%-м и получили 600 г 15%-ного раствора. Сколько граммов каждого раствора взяли?
Решение:
Пусть взяли х г 30%-ного раствора и у г 10%-ного раствора. Тогда можно написать два уравнения:
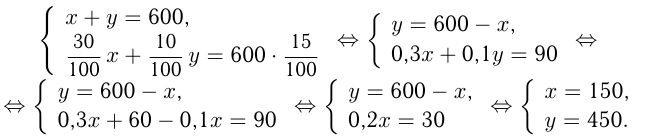
Ответ: взяли 150 г 30%-ного раствора соляной кислоты и 450 г 10%-ного раствора.
Задача №5
Кусок сплава меди и цинка массой 36 кг содержит 45% меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди?
Решение:
В 36 кг сплава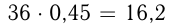 
кг меди. Если добавить х кг меди, то в сплаве меди будет 
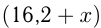кг, а масса всего сплава будет 
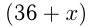кг. По условию
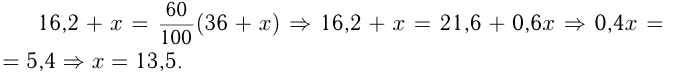
Ответ: нужно добавить 13,5 кг меди.
Следует обратить особое внимание на задачи с вычислением сложных процентов. Это, как правило, задачи с экономическим содержанием. Например, о хранении денег в банке с определенной процентной ставкой.
Эта ссылка возможно вам будет полезна:
Задача №6
В банк положили 2000 рублей под 3% годовых. Каков будет вклад в банке через 5 лет?
Решение:
Через год в банке будет
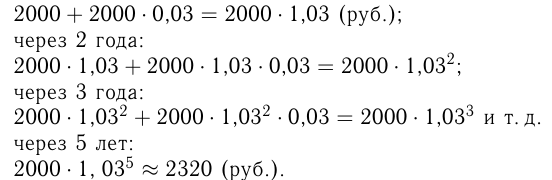
Ответ: в банке будет около 2320 рублей.
Таким образом, если некое количество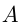 
регулярно увеличивается на определенный постоянный процент 
, то через 
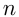этапов будет 
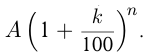Это и есть вычисление сложного процента.
Задача №23
18%-ный раствор соли массой 2 кг разбавили стаканом воды массой 0,25 кг. Какой концентрации раствор в процентах получится?
Решение:
Найдем, сколько соли находится в 2 кг раствора: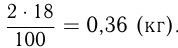 
После добавления воды получили раствор массой 
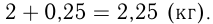Новая концентрация раствора:
Ответ: 16%.
Задача №24
Товар 
до уценки стоил в 1,4 раза дороже, чем товар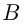 
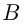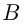. Товар был уценен на 15%, а товар — на 30%. Во сколько раз товар стал дороже товара после уценки?
Решение:
Пусть товар 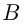стоил до уценки 
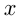рублей, тогда товар стоил до уценки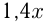 
рублей. После уценки товар стал стоить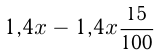 
(руб.), а товар — 
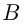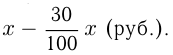
Найдем отношение новых цен товаров:
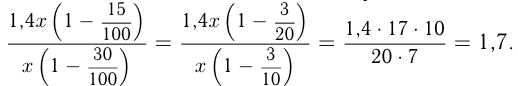
Ответ: в 1,7 раза.
Задача №25
При выпаривании из 8 кг рассола получили 2 кг пищевой соли, содержащей 10% воды. Каков процент содержания воды в рассоле?
Решение:
Пусть в рассоле содержится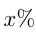 
воды, тогда это составляет 
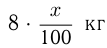воды, т.е. 
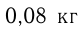воды. При этом чистой соли в растворе 
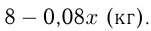В 2 кг соли 
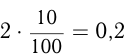кг воды, т. е. чистой соли 
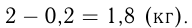Получаем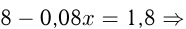 
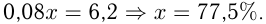
Ответ: 77,5%.
Задача №26
Сумма двух чисел равна 24. Найти меньшее из них, если 35% одного равны 85% другого.
Решение:
Пусть одно из чисел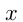 
, тогда другое 
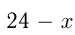. Получаем 
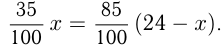. Решаем уравнение:
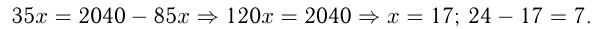
Ответ: меньшее из чисел 7.
Задача №27
Завод увеличивал объем выпускаемой продукции ежегодно на одно и то же число процентов. Найти это число, если за два года объем продукции увеличился на 21%.
Решение:
Пусть каждый год объем продукции увеличивался на 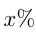, а первоначальный объем продукции . Тогда через 1 год объем продукции стал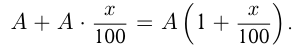 
Через 2 года:
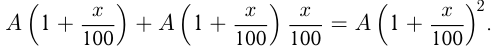Составляем уравнение:
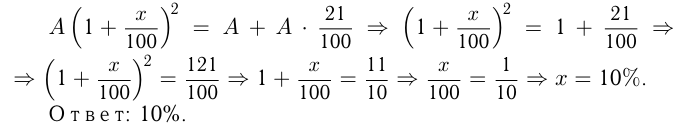
Задача №28
Цену товара первоначально снизили на 20%, затем новую цену снизили еще на 30% и, наконец, еще на 50%. На сколько всего процентов снизили первоначальную цену?
Решение:
Пусть первоначальная цена товара рублей. После 1-го снижения товар стоил: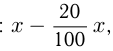 
т. е.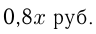 
После 2-го снижения: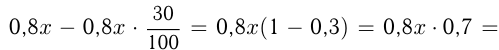 
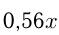руб. После 3-го снижения: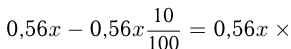 
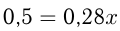руб. Итак, цена уменьшилась на 
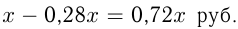, что составляет 72% от первоначальной цены. Ответ: 72%.
Задача №29
Имеется руда двух типов: с содержанием меди 6% и 11%. Сколько руды с меньшим содержанием меди надо взять, чтобы при смешивании с другой рудой получить 20 тонн руды с содержанием меди 8%?
Решение:
Допустим, нужно взять 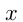тонн более бедной руды и 
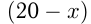тонн более богатой руды. Тогда
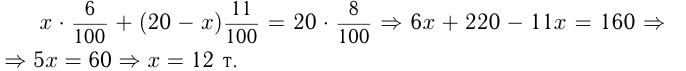
Ответ: нужно взять 12 т бедной руды.
Задача №30
Имеются два куска сплава меди и цинка с процентным содержанием меди 20 и 30% соответственно. В каком отношении нужно взять эти сплавы, чтобы, переплавив взятые куски вместе, получить сплав, содержащий 26% меди?
Решение:
Если 1-го сплава взять 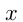кг, а 2-го 
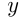кг, то меди в них будет соответственно 
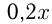кг и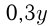 
кг. Сплавленные вместе, они будут весить 
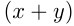кг, и меди в новом куске будет 
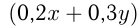кг. Поэтому
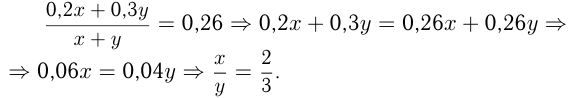
Ответ: в отношении 2 : 3.
Задача №31
Выработка продукции за год работы предприятия возросла на 4%. На следующий год она увеличилась на 8%. Определить средний ежегодный прирост продукции за этот период.
Решение:
Пусть средний прирост 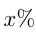, тогда если первоначальная продукция , то через 2 года стало:
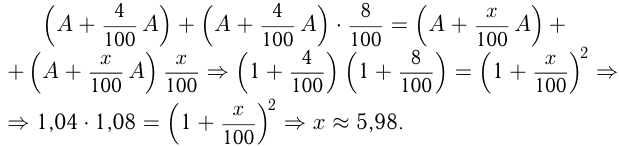
Ответ: средний ежегодный прирост около 6%.
Задача №32
В сосуд налито 4 литра 70%-го раствора серной кислоты. Во второй такой сосуд налито 3 литра 90%-го раствора серной кислоты. Сколько литров раствор нужно перелить из второго сосуда в первый, чтобы в нем получился 74%-й раствор серной кислоты? Емкости сосудов не менее 7 литров.
Решение:
Допустим, нужно перелить 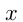л раствора из 2-го сосуда в 1-й. В 1-м сосуде 
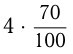чистой серной кислоты, в 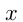литрах из 2-го сосуда 
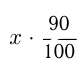л чистои серной кислоты, тогда в 1-м сосуде будет 
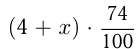чистой серной кислоты. Следовательно: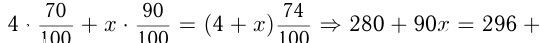 
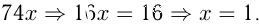
Ответ: нужно перелить 1 литр раствора.
Задача №33
Цена на товар была повышена на 25%. На сколько процентов надо после этого ее снизить, чтобы получить первоначальную цену товара?
Решение:
Пусть 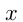— первоначальная цена товара, тогда 
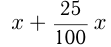— повышенная цена. Пусть новую цену нужно снизить на 
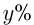. Запишем уравнение: 1 / 1 \ у
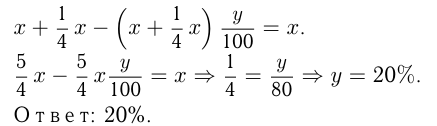
Задача №34
Руда содержит 40% примесей, а выплавленный из нее металл содержит 4% примесей. Сколько получится металла из 24 т руды?
Решение:
Руда без примесей составляет: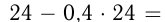 
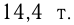Если 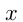т — количество металла из 24 т руды, то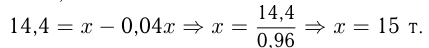
Ответ: 15 тонн металла.
Эта ссылка возможно вам будет полезна:
Задача №35
Ежегодный прирост населения города составляет 20%. Через сколько лет население города удвоится?
Решение:
Пусть чел. — население города в некоторый момент времени. Тогда через 1 год население составит: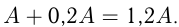 
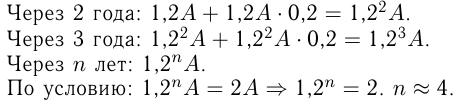
Ответ: население города удвоится через 4 года.
Задача №36
Выработка продукции за год работы предприятия возросла на 8%, а за следующий год она увеличилась на 47%. Найти средний годовой прирост продукции за этот период.
Решение:
Пусть — первоначальный объем продукции, тогда через год: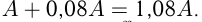 
Через 2 года: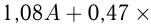 
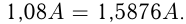Если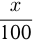 
средний годовой прирост продукции, то через 1 год объем продукции 
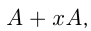через 2 года 
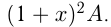Из условия
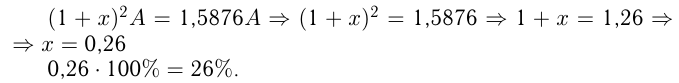
Ответ: средний годовой прирост продукции 26%.
Задача №37
Имеются два сплава, состоящие из цинка, меди и олова. Известно, что 1-й сплав содержит 40% олова, а 2-й — 26% меди. Процентное содержание цинка в 1-м и 2-м сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Определить, сколько олова содержится в новом сплаве.
Решение:
Составим таблицу:
Это таблица процентного, или долевого содержания 3-х компонентов в 2-х сплавах. В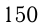 
кг 1-го сплава 
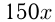кг цинка, в 
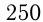кг 2-го сплава 
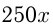кг цинка. Поэтому в новом сплаве 
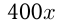кг цинка. По условию 
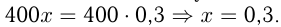Олова в 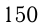кг 1-го сплава 
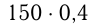кг, в 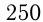кг 2-го сплава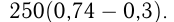 
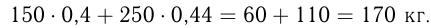
Ответ: 170 кг.
Задача №38
Имеются 2 слитка золота с серебром. Процентное содержание золота в 1-м слитке в 2,5 раза больше, чем процентное содержание золота во 2-м слитке. Если сплавить оба слитка вместе, то получится слиток, в котором будет 40% золота. Найти, во сколько раз 1-й слиток тяжелее второго, если известно, что при сплавлении равных по весу частей первого и второго слитков получается слиток, в котором содержится 35% золота.
Решение:
Допустим, первый слиток весит 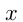кг и содержит 
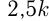частей золота, второй слиток весит 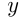кг и содержит 
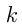частей
золота. Тогда новый слиток весит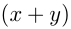 
кг и содержит 
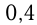части золота. Имеем уравнения:
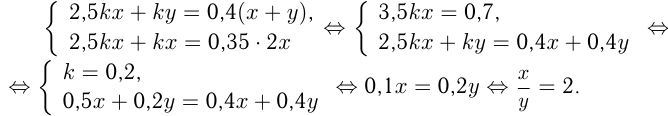
Ответ: 1-й слиток тяжелее 2-го в 2 раза.
Задача №39
Известно, что вклад, находящийся в банке с начала года, возрастает к концу года на определенный процент (свой для каждого банка). В начале года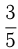 
некоторого количества денег положили в 1-й банк, а оставшуюся часть во 2-й банк. К концу года сумма этих вкладов стала равна 590 денежным единицам, к концу следующего года 701 денежной единице. Было подсчитано, что если бы первоначально 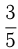исходного количества денег положили во 2-й банк, а оставшуюся часть в 1-й банк, то по истечении одного года сумма вкладов в эти банки стала бы равной 610 денежным единицам. Какова в этом случае была бы сумма вкладов в эти банки к концу второго года?
Решение:
Пусть — общая первоначальная сумма денег.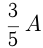
положили в 1-й банк, — 
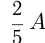2-й банк; 
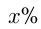и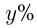 
— соответствующие процентные ставки 1-го и 2-го банков. Тогда из условий получаем систему уравнений:
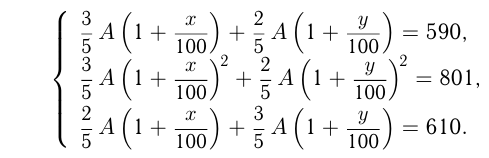
Нужно определить
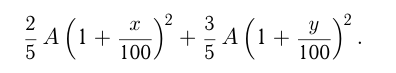
При решении системы примем:
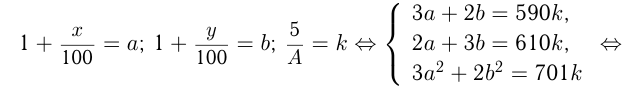
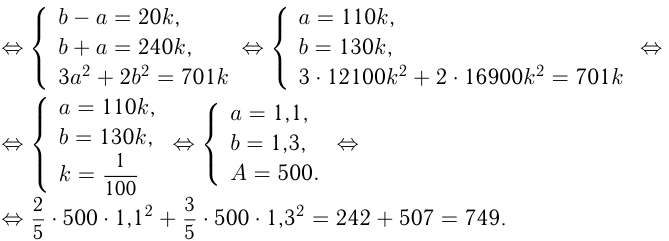
Ответ: сумма вкладов равнялась бы 749 денежным единицам.
Задача №40
Свежие фрукты содержат 72% воды, а сухие 20%. Сколько сухих фруктов получится из 20 кг свежих фруктов?
Решение:
В 20 кг свежих фруктов содержится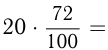 
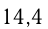кг воды, а, значит, сухого вещества 
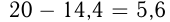кг. Допустим, из 20 кг свежих фруктов получится 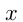кг сухих , фруктов. Тогда в них 
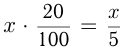— кг воды и сухого вещества
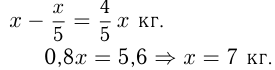
Ответ: 7 кг сухих фруктов.
Задача №41
Имеются два раствора серной кислоты в воде: 1-й — 40%-й, а 2-й — 60%-й. Эти два раствора смешали, после чего добавили 5 кг чистой воды и получили 20%-й раствор. Если бы вместо 5 кг чистой воды добавили 5 кг 80%-го раствора, то получился бы 70%-й раствор. Сколько было 70%-го и 60%-го растворов?
Решение:
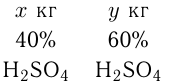
В 1-м растворе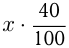 
чистои кислоты, во 2-м растворе 
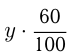чистой кислоты, из первого условия получаем 
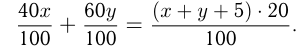В 5 кг 80%-го раствора 
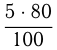чистой серной кислоты, поэтому из второго условия получаем
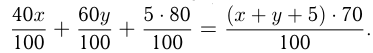
Имеем систему:
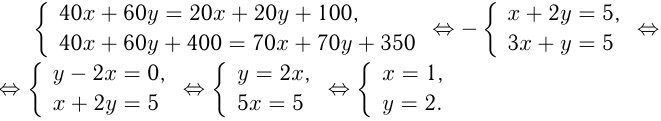
Ответ: 1 кг 40%-го раствора и 2 кг 60%-го раствора.
Задача №42
Сплавляя два одинаковых по весу куска чугуна с разным содержанием хрома, получили сплав, в котором содержалось 12 кг хрома. Если бы 1-й кусок был в 2 раза тяжелее, то в сплаве содержалось бы 16 кг хрома. Известно, что содержание хрома в 1-м куске на 5% меньше, чем во 2-м. Найти процентное содержание хрома в каждом куске чугуна.
Решение:
Если вес каждого куска чугуна кг, а содержание хрома в 1-м куске 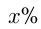, а во 2-м —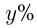, то получим систему:
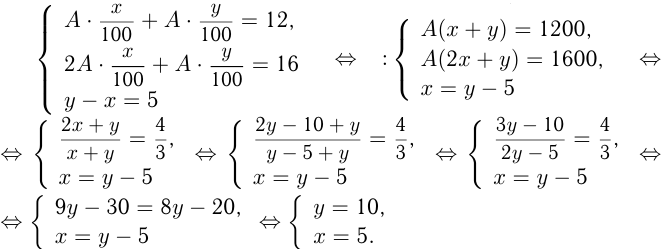
Ответ: в 1-м куске 5% хрома, во 2-м — 10% хрома.
Задача №43
Имеются два бака: 1-й бак наполнен чистым глицерином, 2-й бак — водой. Взяли 2 трехлитровых ковша, зачерпнули 1-м ковшом глицерин из 1-го бака, а 2-м ковшом — воду из 2-го бака, после чего 1-й ковш влили во 2-й бак, а 2-й ковш — в 1-й бак. Затем после перемешивания снова зачерпнули 1-м ковшом смесь из 1-го бака, а 2-м ковшом — смесь из 2-го бака и влили 1-й ковш во 2-й бак, а 2-й ковш в 1-й бак. В результате половину объема 1-го бака занял чистый глицерин. Найти объемы баков, если известно, что их суммарный объем в 10 раз больше объема 1-го бака.
Решение:
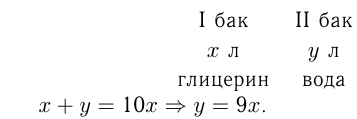
На 1-м этапе в I баке осталось 
л глицерина, во II баке стало 3 л глицерина. На 2-м этапе из I бака взяли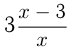 
— л глицерина, т.к. доля глицерина в I баке 
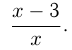В I бак добавили 
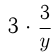л. глицерина, т.к. доля глицерина во II баке 
.
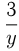По условию
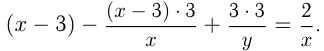
Получаем систему:
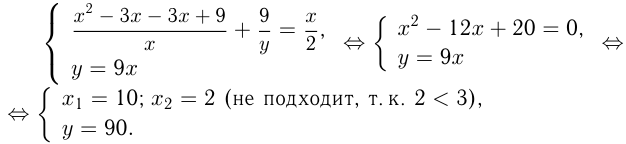
Ответ: 10 литров и 90 литров.
Задача №44
Для приготовления смеси из двух жидкостей и были взяты два сосуда емкостью по 15 л каждый, в которых находилось всего 15 л жидкости . Затем 1-й сосуд доверху долили жидкостью , и было произведено перемешивание. После этого 2-й сосуд дополнили доверху смесью из 1-го сосуда. Затем из второго сосуда отлили в 1-й 6 л получившейся смеси. После этого в 1-м сосуде оказалось жидкости на 1 л больше, чем во 2-м. Сколько литров жидкости было первоначально во 2-м сосуде?
Решение:
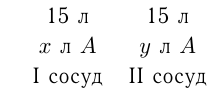
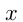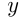Пусть в 1-м сосуде л жидкости , а во 2-м сосуде л жидкости , причем из условия 
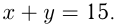В 1-й сосуд долили 
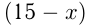л жидкости 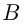. Доля жидкости в 1-м сосуде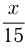 
доля жидкости 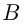в 1-м сосуде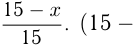 
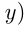л смеси взяли из 1-го сосуда; в этой смеси 
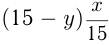л жидкости . Во 2-м сосуде стало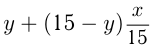 
жидкости ; доля жидкости во 2-м сосуде
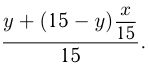В 6 л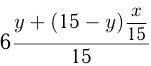 
л жидкости .
В 1-м сосуде перед добавлением 6 л было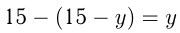 
л, в них жидкости 
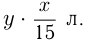
Получаем систему уравнении:
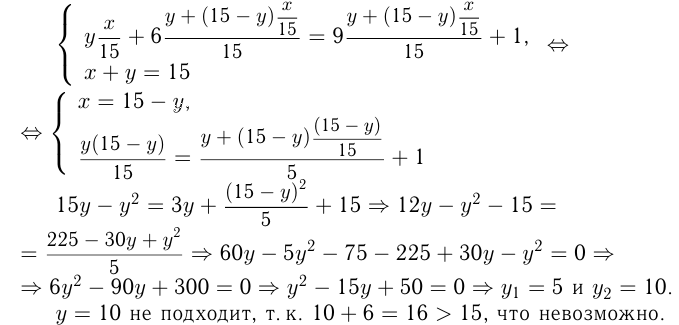
Ответ: во 2-м сосуде было 5 л жидкости .
Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Решение систем уравнений и неравенств |
| Решение задач на проценты по математике |
| Решение задач на движение по математике |
| Решение задач на работу по математике |
