Оглавление:
Следующий тип рассматриваемых задач — это задачи на работу. Несмотря на существенные отличия в тексте, решение задач этого типа аналогично решению задач на движение. Аналогия заключается в следующем: если обозначить весь объем выполняемых работ — 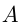 , производительность труда —
, производительность труда — 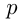 и
и 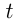 — время выполнения работы, то можно записать:
— время выполнения работы, то можно записать: 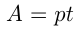 и, следовательно
и, следовательно 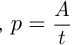 и
и 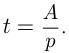 Несмотря на новые обозначения, это те же формулы, что и в задачах на движение. Производительность труда — это количество совершенной работы в единицу времени,
Несмотря на новые обозначения, это те же формулы, что и в задачах на движение. Производительность труда — это количество совершенной работы в единицу времени,
например, объем выкопанного грунта за день, количество об-
работанных деталей в час, количество посаженных деревьев за
неделю и т.п. Таким образом, работа 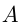 — аналог пути
— аналог пути 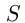 , производительность труда (иногда говорят — мощность) — аналог скорости
, производительность труда (иногда говорят — мощность) — аналог скорости 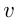 .
.
Задача №10
Тракторная бригада может вспахать 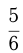 участка земли за 4 ч 15 мин. До обеденного перерыва бригада работала 4,5 ч, после чего остались невспаханными еще 8 га. Как велик был участок?
участка земли за 4 ч 15 мин. До обеденного перерыва бригада работала 4,5 ч, после чего остались невспаханными еще 8 га. Как велик был участок?
Решение:
Пусть площадь участка 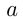 га, тогда
га, тогда 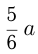 бригада вспахивает за
бригада вспахивает за 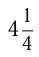 ч, и ее производительность:
ч, и ее производительность: 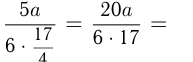
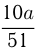 (га/ч). За 4,5 ч, работая с этой производи-тельностью, бригада вспахала
(га/ч). За 4,5 ч, работая с этой производи-тельностью, бригада вспахала 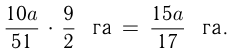 Составим уравнение:
Составим уравнение: 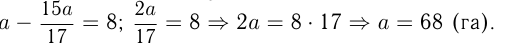
Ответ: площадь участка 68 га.
Задача №11
Однотипные детали обрабатываются на 2-х станках. Производительность 1-го станка на 40% больше производительности 2-го. Сколько деталей было обработано за смену каждым станком, если 1-й станок работал 6 часов, а 2-й — 8 часов, причем оба станка вместе обработали 820 деталей?
Решение:
Обозначим производительность 2-го станка 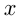 дет./ч, тогда производительность 1-го станка
дет./ч, тогда производительность 1-го станка 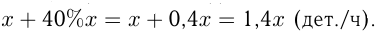 Из условий составим уравнение:
Из условий составим уравнение:
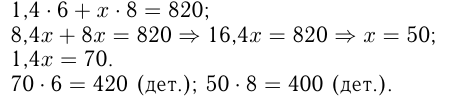
Ответ: 1-й станок обработал 420 деталей, а 2-й — 400 деталей.
Задача №12
В одном бассейне имеется 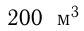 воды, а в другом
воды, а в другом 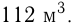 Открывают краны, через которые наполняются бассейны. Через сколько часов количество воды в бассейнах будет одинаковым, если во 2-й бассейн вливается в час на
Открывают краны, через которые наполняются бассейны. Через сколько часов количество воды в бассейнах будет одинаковым, если во 2-й бассейн вливается в час на 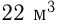 больше воды, чем в 1-й?
больше воды, чем в 1-й?
Решение:
Допустим, в 1-й бассейн вливается в час 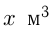 воды, тогда во 2-й бассейн вливается в час
воды, тогда во 2-й бассейн вливается в час 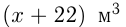 воды. Допустим также, что выравнивание количества воды в бассейнах произойдет через t часов. Составим уравнение, исходя из условий задачи:
воды. Допустим также, что выравнивание количества воды в бассейнах произойдет через t часов. Составим уравнение, исходя из условий задачи:
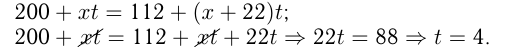
Ответ: через 4 часа.
Задача №13
Двое рабочих, из которых второй начал работать на 1,5 дня позже первого, работая независимо один от другого, оклеили обоями несколько комнат за 7 дней, считая с момента выхода на работу первого рабочего. Если бы эта работа была поручена каждому рабочему отдельно, то первому для ее выполнения понадобилось бы на 3 дня больше, чем второму. За сколько дней каждый из них отдельно выполнил бы эту же работу?
Решение:
Допустим, 1-й рабочий выполнил работу за 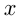 дней, а 2-й — за
дней, а 2-й — за 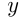 дней, выполненная работа —
дней, выполненная работа — 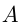 комнат. Тогда производительность 1-го рабочего
комнат. Тогда производительность 1-го рабочего 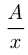 комн./день; 2-го рабочего
комн./день; 2-го рабочего 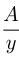 комн./день. Исходя из условий, составляем систему:
комн./день. Исходя из условий, составляем систему:
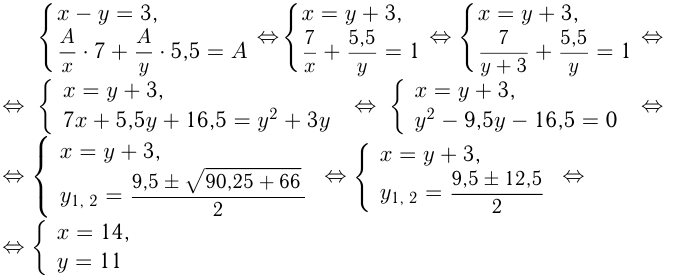
(отрицательное 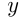 не имеет смысла).
не имеет смысла).
Ответ: за 14 дней и 11 дней.
Задача №73
Бассейн при одновременном включении 4-х кранов заполняется водой за 45 мин. За сколько минут тот же бассейн может заполниться водой при одновременном включении 6-ти таких кранов?
Решение. Пусть объем бассейна 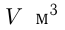 , а производительность (мощность) каждого крана
, а производительность (мощность) каждого крана 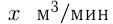 , тогда
, тогда 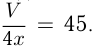
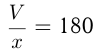 ; нужно найти
; нужно найти 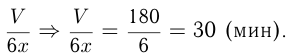
Ответ: бассейн заполнится за 30 мин.
Задача №74
Две бригады должны были закончить уборку урожая за 12 дней. После 8 дней совместной работы 1-я бригада получила другое задание, поэтому 2-я бригада одна закончила уборку за 7 дней. За сколько дней могла бы убрать урожай каждая бригада, работая отдельно?
Решение. Обозначим весь урожай 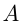 тонн; производительность труда 1-й бригады
тонн; производительность труда 1-й бригады 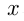 , а производительность 2-й бригады
, а производительность 2-й бригады 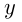 т/день. Совместная производительность
т/день. Совместная производительность 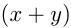 т/день. Отсюда:
т/день. Отсюда:

Задача №75
Из резервуара идут три трубы. Через первые две трубы содержимое резервуара откачивается за 1 ч 10 мин, через первую и третью за 1 ч 24 мин, а через вторую и третью за 2 ч 20 мин. За какое время содержимое резервуара откачивается всеми трубами вместе?
Решение. Пусть объем резервуара 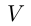 , тогда нужно определить
, тогда нужно определить 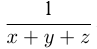 , где
, где 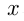 ,
, 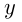 и
и 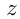 мощности труб, выраженные в соответствующих единицах.
мощности труб, выраженные в соответствующих единицах.
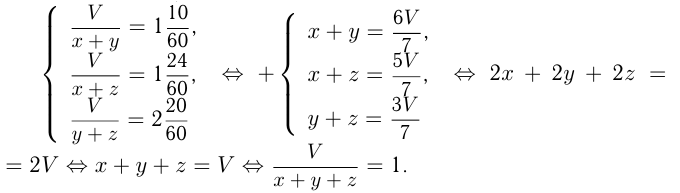
Ответ: все трубы вместе будут работать 1 час.
Задача №76
Две трубы, действуя вместе в течение 1 часа, наполняют водой 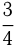 бассейна. Если сначала 1-я труба наполнит
бассейна. Если сначала 1-я труба наполнит 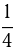 бассейна, а затем вторая при выключенной первой доведет объем воды до
бассейна, а затем вторая при выключенной первой доведет объем воды до 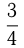 бассейна, то на это понадобится 2,5 часа. Если 1-ю трубу включить на 1 час, а вторую на 0,5 часа, то они наполнят бассейн более, чем наполовину. За какое время наполнит бассейн каждая труба?
бассейна, то на это понадобится 2,5 часа. Если 1-ю трубу включить на 1 час, а вторую на 0,5 часа, то они наполнят бассейн более, чем наполовину. За какое время наполнит бассейн каждая труба?
Решение. Пусть объем бассейна 1 куб. ед., 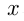 и
и 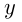 куб. ед./ч — мощности труб. Из условий:
куб. ед./ч — мощности труб. Из условий:
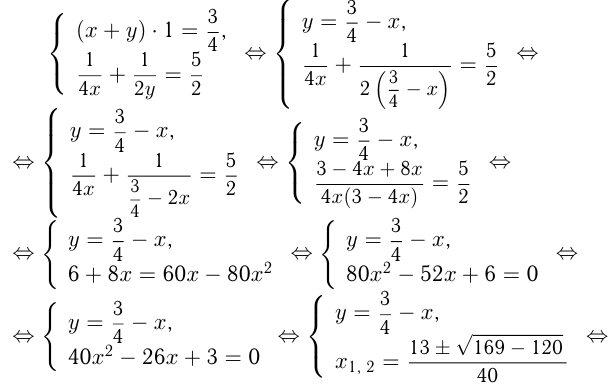
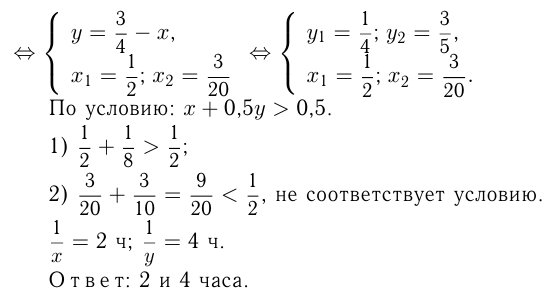
Задача №77
Два экскаватора разной конструкции должны проложить две траншеи одинакового сечения длиной 960 м и 180 м. Вся работа продолжалась 22 дня, в течение которых 1-й экскаватор рыл большую траншею. 2-й экскаватор начал работать на 6 дней позднее 1-го, отрыл меньшую траншею, 3 дня ремонтировался и затем помогал 1-му. Если не нужно было бы тратить времени на ремонт, то работа была бы закончена за 21 день. Какова производительность каждого экскаватора в м/день?
Решение. Пусть 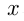 и
и 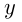 м/день — производительность экскаваторов. За 22 дня 1-й экскаватор вырыл
м/день — производительность экскаваторов. За 22 дня 1-й экскаватор вырыл 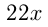 м, осталось в первой траншее вырыть
м, осталось в первой траншее вырыть 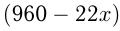 м. 2-й экскаватор работал
м. 2-й экскаватор работал 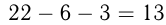 дней и вырыл
дней и вырыл 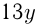 м. По условию
м. По условию 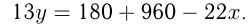 Если бы не было ремонта, то 1-й экскаватор вырыл бы
Если бы не было ремонта, то 1-й экскаватор вырыл бы 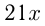 м, а 2-й —
м, а 2-й —  м, т.е.
м, т.е. 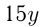 м. По условию:
м. По условию: 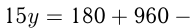
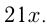
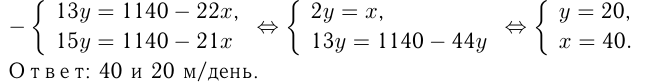
Задача №78
Три тракторные бригады вместе вспахивают поле за 4 дня. Это же поле 1-я и 2-я бригады вместе вспахивают за 6 дней, а 1-я и 3-я бригады вместе — за 8 дней. Во сколько раз больше площадь, вспахиваемая за день 2-й бригадой, по сравнению с площадью, вспахиваемой за день 3-й бригадой?
Решение. Пусть 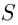 га — площадь поля;
га — площадь поля; 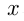 ,
, 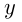 и
и 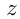 га/день — производительности труда бригад. Тогда:
га/день — производительности труда бригад. Тогда:
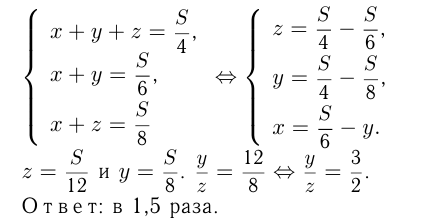
Задача №79
Два насоса различной мощности, работая вместе, наполняют бассейн за 4 часа. Для наполнения бассейна наполовину 1-му насосу требуется времени на 4 часа больше, чем 2-му насосу для наполнения бассейна на три четверти. За какое время может наполнить бассейн каждый насос в отдельности?
Решение. Пусть 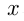 — мощность 1-го насоса и
— мощность 1-го насоса и 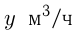 — мощность 2-го насоса, тогда
— мощность 2-го насоса, тогда 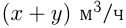 — их общая мощность.
— их общая мощность. 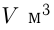 — объем бассейна.
— объем бассейна.
Тогда имеем систему уравнений:

Задача №80
В бак может поступать вода через одну из двух труб.
Через 1-ю трубу бак можно наполнить на 1 час быстрее, чем через 2-ю трубу. Если бы емкость бака была больше на 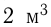 , а пропускная способность 2-й трубы была бы больше на
, а пропускная способность 2-й трубы была бы больше на 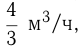 то для наполнения бака через 2-ю трубу понадобилось бы столько же времени, сколько требуется для пропуска
то для наполнения бака через 2-ю трубу понадобилось бы столько же времени, сколько требуется для пропуска 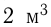 через 1- ю трубу. Какова емкость бака, если известно, что за время его
через 1- ю трубу. Какова емкость бака, если известно, что за время его
наполнения через 2-ю трубу через 1-ю трубу могло поступить 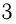
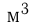 воды?
воды?
Решение:
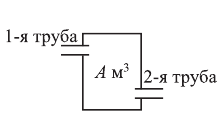
Пусть емкость бака 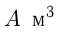 , мощность 1-й трубы (пропускная способность)
, мощность 1-й трубы (пропускная способность) 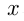 , мощность 2-й трубы
, мощность 2-й трубы 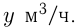 Из условий задачи получаем систему трех уравнений:
Из условий задачи получаем систему трех уравнений:
Эта ссылка возможно вам будет полезна:
Задача №81
В бассейн может поступать вода через пять труб. Первые три трубы, работая вместе, наполняют бассейн за 3 ч, 4-я и 5-я вместе с 1-й — за 2 ч, 3-я и 4-я — за 6 ч, 2-я и 5-я — за 4 ч. За сколько времени наполняют бассейн все пять труб вместе? Решение.
Пусть 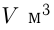 — объем бассейна;
— объем бассейна;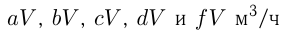 — мощности пяти труб, где
— мощности пяти труб, где 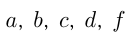 определяют части объема бассейна, наполняемые каждой трубой за 1 час. Тогда:
определяют части объема бассейна, наполняемые каждой трубой за 1 час. Тогда:
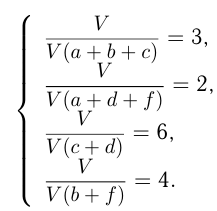
Нужно определить
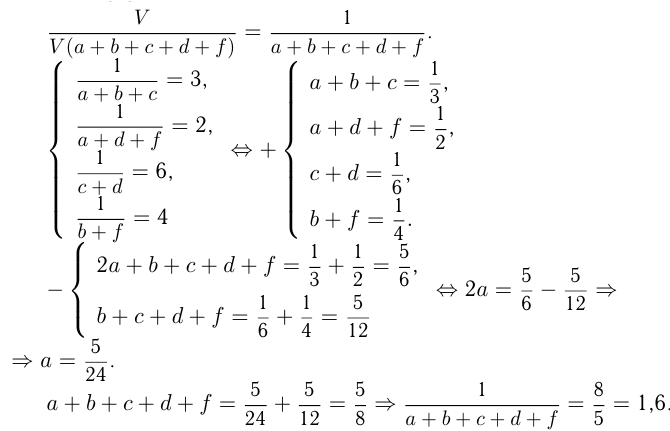
Ответ: пять труб наполнят бассейн за 1 час 36 мин.
Задача №82
Каждый из рабочих должен был изготовить 36 одинаковых деталей. 1-й рабочий приступил к выполнению своего задания на 4 мин позже 2-го, но 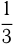 задания они выполнили одновременно. Полностью выполнив свое задание, 1-й рабочий после двухминутного перерыва снова приступил к работе и к моменту выполнения задания 2-м рабочим изготовил еще 2 детали. Сколько деталей в час изготавливал каждый рабочий?
задания они выполнили одновременно. Полностью выполнив свое задание, 1-й рабочий после двухминутного перерыва снова приступил к работе и к моменту выполнения задания 2-м рабочим изготовил еще 2 детали. Сколько деталей в час изготавливал каждый рабочий?
Решение. Пусть 1-й рабочий изготавливал 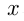 , а 2-й —
, а 2-й — 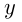
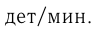
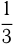 задания — это 12 деталей. Поэтому 1-е уравнение
задания — это 12 деталей. Поэтому 1-е уравнение 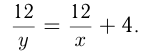 1-й рабочий сделал 26 деталей и отдыхал 2 мин, а 2-й сделал
1-й рабочий сделал 26 деталей и отдыхал 2 мин, а 2-й сделал 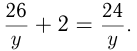
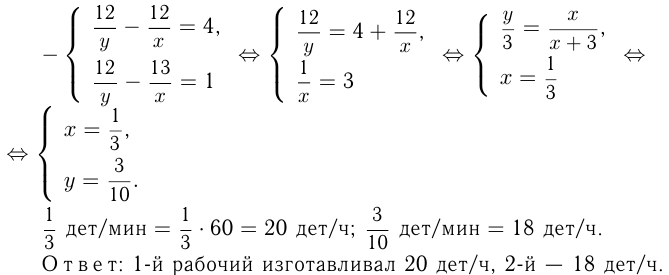
Задача №83
Мастер, работая вместе с учеником, помог выполнить часть задания, а затем прекратил свою работу. Оставшуюся часть задания ученик закончил один. В результате время, затраченное на выполнение задания, оказалось в 3 раз меньше времени, необходимого ученику для выполнения этого задания им одним. Во сколько раз мастер затратил бы больше времени, выполняя один все задание, по сравнению с тем временем, которое он затратил на помощь ученику?
Решение. Пусть 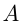 изделий — все задание;
изделий — все задание; 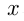 — производительность мастера,
— производительность мастера, 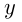
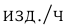 — производительность ученика;
— производительность ученика;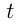 ч — время, которое затратил мастер на помощь ученику. Тогда мастер вместе с учеником сделали
ч — время, которое затратил мастер на помощь ученику. Тогда мастер вместе с учеником сделали 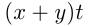 изделий, и осталось сделать
изделий, и осталось сделать 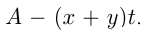 На изготовление этих изделий ученик затратил
На изготовление этих изделий ученик затратил 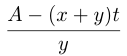 — часов. Из условия
— часов. Из условия
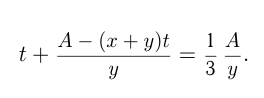
Мастер, выполняя один все задание, потратил бы 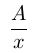 часов, поэтому нужно определить
часов, поэтому нужно определить 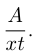
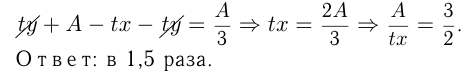
Задача №84
Две бригады учащихся, работая совместно, закончили посадку деревьев на учебно-опытном участке за 4 дня. Сколько дней потребовалось бы на выполнение этой работы каждой бригаде отдельно, если бы одна из бригад могла закончить посадку деревьев на 6 дней раньше другой?
Решение. Пусть нужно было посадить 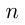 деревьев;
деревьев; 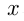 — производительность 1-й бригады,
— производительность 1-й бригады, 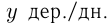 — производительность 2-й. Тогда из условий:
— производительность 2-й. Тогда из условий:

Задача №85
Двое рабочих совместно могут выполнить плановое задание за 12 дней. Если половину задания будет выполнять один рабочий, а затем 2-ю половину — другой, то все задание будет выполнено за 25 дней. За сколько дней может выполнить задание каждый рабочий?
Решение. Пусть 1-й рабочий выполнит задание за 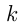 , а 2-й — за
, а 2-й — за 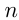 дней.
дней. 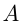 изделий — все задание. Тогда
изделий — все задание. Тогда 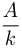 -производительность 1-го рабочего, а
-производительность 1-го рабочего, а 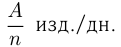 — производительность 2-го. Отсюда два уравнения:
— производительность 2-го. Отсюда два уравнения:
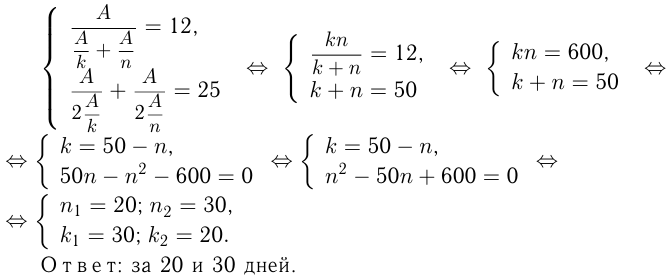
Задача №86
В одном бассейне имеется 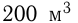 воды, а в другом —
воды, а в другом — 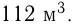 Открывают краны, через которые наполняются бассейны. Через сколько часов количество воды в бассейнах будет одинаковым, если во 2-й бассейн вливается в час на
Открывают краны, через которые наполняются бассейны. Через сколько часов количество воды в бассейнах будет одинаковым, если во 2-й бассейн вливается в час на 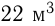 воды больше, чем в 1-й?
воды больше, чем в 1-й?
Решение. Пусть 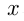 — мощность 1-го крана, тогда
— мощность 1-го крана, тогда 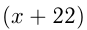
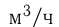 — мощность 2-го крана. По условию:
— мощность 2-го крана. По условию: 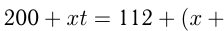
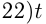 , где
, где 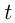 ч — время наполнения бассейнов до одинакового состояния.
ч — время наполнения бассейнов до одинакового состояния.
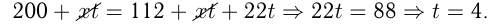
Ответ: через 4 часа.
Задача №87
Бригада монтеров могла окончить электропроводку в 4 часа дня, прокладывая в час по 8 м. После выполнения половины всего задания один рабочий выбыл из бригады; в связи с этим бригада стала прокладывать в час по 6 м и закончила работу в 6 часов вечера. Сколько метров провода было проложено и за сколько часов?
Решение. Допустим, было проложено 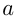 м провода, и работа продолжалась
м провода, и работа продолжалась 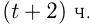 ., где
., где 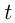 ч. — ранее запланированное время.Тогда из условий получаем 2 уравнения:
ч. — ранее запланированное время.Тогда из условий получаем 2 уравнения:
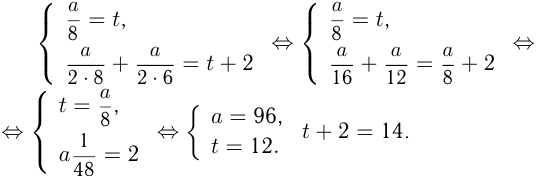
Ответ: было проложено 96 метров провода за 14 часов.
Задача №88
Двум рабочим было поручено изготовить партию одинаковых деталей. После того, как 1-й проработал 2 часа, а 2-й 5 часов, оказалось, что они выполнили половину всей работы. Проработав совместно еще 3 часа, они установили, что им осталось выполнить 0,05 всей работы. За какой промежуток времени каждый из них, работая отдельно, может выполнить всю работу?
Решение. Допустим, нужно было изготовить 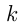 деталей;
деталей; 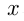 — производительность 1-го рабочего;
— производительность 1-го рабочего; 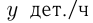 — производительность 2-го. Условия позволяют составить два уравнения:
— производительность 2-го. Условия позволяют составить два уравнения:
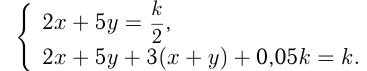
Нужно определить 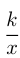 и
и 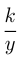 .
.
Задача №89
Два одинаковых бассейна одновременно начали наполняться водой. В 1-й бассейн поступает в час на 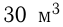 больше воды, чем во 2-й. В некоторый момент в 2-х бассейнах вместе оказалось столько воды, сколько составляет объем каждого из них. После этого через 2 ч 40 мин наполнился 1-й бассейн, а еще через 3 ч 20 мин — 2-й. Сколько воды поступало в час в каждый бассейн?
больше воды, чем во 2-й. В некоторый момент в 2-х бассейнах вместе оказалось столько воды, сколько составляет объем каждого из них. После этого через 2 ч 40 мин наполнился 1-й бассейн, а еще через 3 ч 20 мин — 2-й. Сколько воды поступало в час в каждый бассейн?
Решение. Пусть во 2-й бассейн поступает 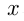 , а в 1-й —
, а в 1-й — 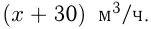 Объем одного бассейна
Объем одного бассейна 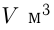 ;
; 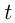 ч. — время до промежуточного момента. Тогда имеем:
ч. — время до промежуточного момента. Тогда имеем:
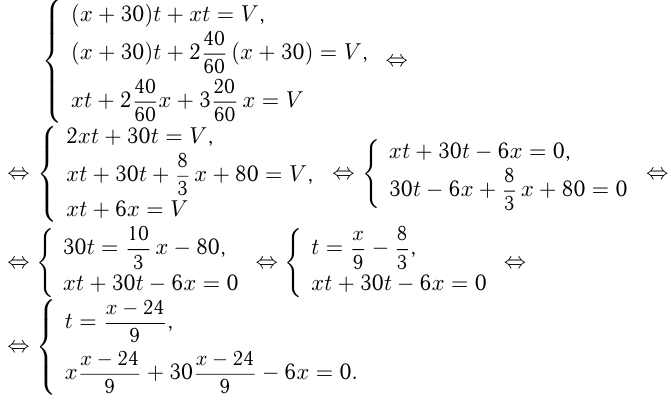
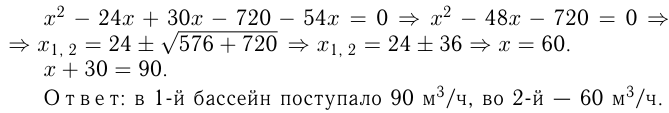
Задача №90
В бассейн проведены две трубы разного сечения. Одна — равномерно подающая, другая — равномерно отводящая воду, причем через 1-ю бассейн наполняется на 2 часа дольше, чем через 2-ю опорожняется. При заполненном на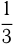 бассейне были открыты обе трубы, и бассейн оказался пустым через 8 часов. За сколько часов, действуя отдельно, 1-я труба наполняет бассейн, а 2-я его опорожняет?
бассейне были открыты обе трубы, и бассейн оказался пустым через 8 часов. За сколько часов, действуя отдельно, 1-я труба наполняет бассейн, а 2-я его опорожняет?
Решение:
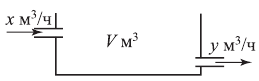
Объем бассейна 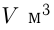 ; мощность 1-й трубы —
; мощность 1-й трубы — 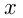 ; мощность 2-й —
; мощность 2-й — 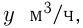
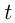 ч — время опорожнения бассейна. Тогда условия дают следующую систему уравнений:
ч — время опорожнения бассейна. Тогда условия дают следующую систему уравнений:
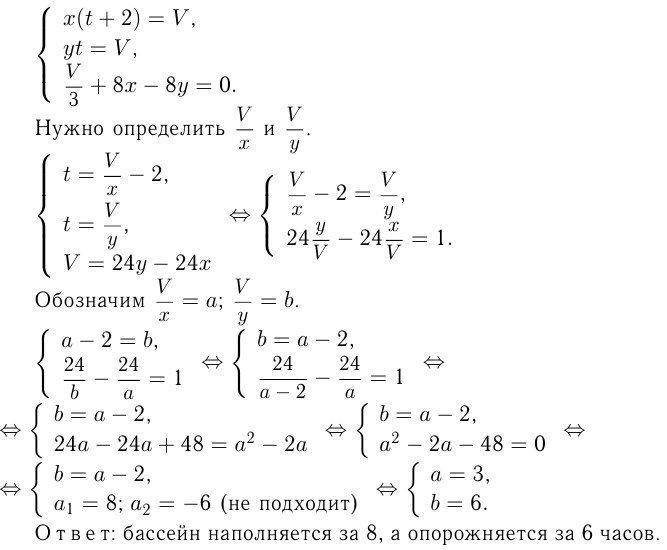
Задача №91
Два «механических крота» разной мощности при одновременной работе с разных концов тоннеля могли бы прорыть его за 5 дней. В действительности же оба «крота» были применены последовательно с одной стороны тоннеля, причем 1-й прорыл 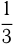 , а 2-й — остальные
, а 2-й — остальные 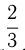 его длины. На выполнение всей работы ушло при этом 10 дней. За сколько дней каждый «крот», работая самостоятельно, мог бы прорыть тоннель?
его длины. На выполнение всей работы ушло при этом 10 дней. За сколько дней каждый «крот», работая самостоятельно, мог бы прорыть тоннель?
Решение:
Пусть длина тоннеля 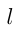 м,
м, 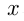 — мощность 1-го «крота»,
— мощность 1-го «крота», 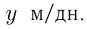 — мощность 2-го. Условия дают следующие уравнения:
— мощность 2-го. Условия дают следующие уравнения:
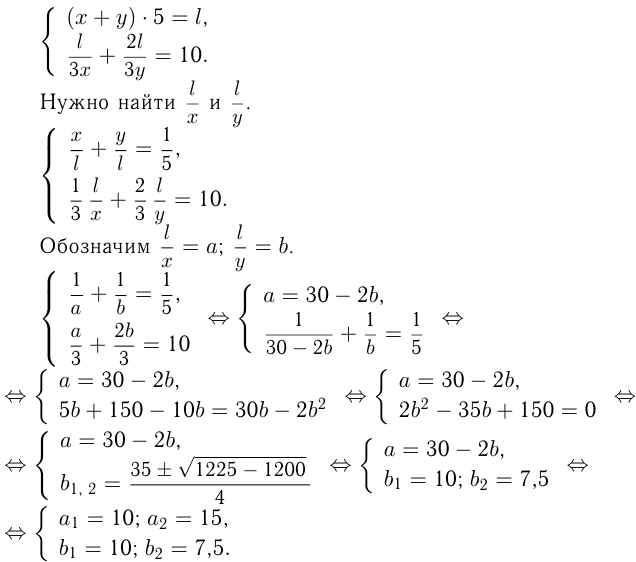
Первая пара 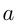 и
и 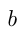 не подходит, т.к. по условию «кроты» имеют разную мощность.
не подходит, т.к. по условию «кроты» имеют разную мощность.
Ответ: за 15 и 7,5 дней.
Задача №92
Три автоматические линии выпускают одинаковую продукцию, но имеют разную производительность. Производительность всех трех одновременно действующих линий в 1,5 раза выше производительности 1-й и 2-й линий, работающих одновременно. Сменное задание для 1-й линии 2-я и 3-я линии, работая одновременно, могут выполнить на 4 ч 48 мин быстрее, чем его выполняет 1-я линия; это же задание 2-я линия выполняет на 2 часа быстрее, чем 1-я линия. Найти время выполнения 1-й линией своего сменного задания.
Решение:
Допустим, 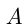 изделий — сменное задание первой линии;
изделий — сменное задание первой линии; 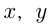 и
и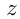 изд./ч — производительность 1-й, 2-й и 3-й линий. Условия задачи приводят к системе уравнений:
изд./ч — производительность 1-й, 2-й и 3-й линий. Условия задачи приводят к системе уравнений:

Задача №93
Три сенокосилки участвовали в покосе травы с поля площадью 25 га. За 1 час 1-я сенокосилка скашивает 3 га, 2-я — на 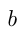 га меньше 1-й, а 3-я — на
га меньше 1-й, а 3-я — на 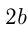 га больше 1-й. Сначала работали одновременно 1-я и 2-я сенокосилки и скосили 11 га, а затем оставшуюся часть площади скосили, работая одновременно, 1-я и 3-я сенокосилки. Определить значение
га больше 1-й. Сначала работали одновременно 1-я и 2-я сенокосилки и скосили 11 га, а затем оставшуюся часть площади скосили, работая одновременно, 1-я и 3-я сенокосилки. Определить значение 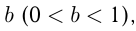 при котором все поле скошено за 4 часа, если работа велась без перерыва.
при котором все поле скошено за 4 часа, если работа велась без перерыва.
Решение:
Известно, что производительность 1-й сенокосилки 3, 2-й 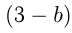 и
и 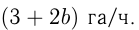 По условию
По условию
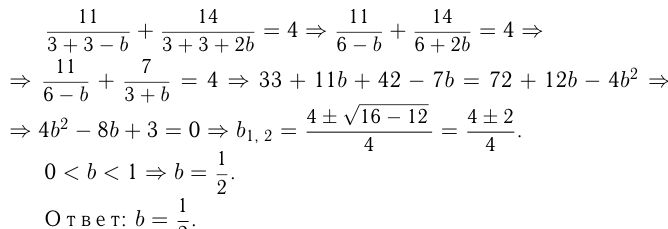
Задача №94
Бригада рыбаков планировала выловить в определенный срок 1800 ц рыбы. В течение 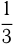 этого срока был шторм, вследствие чего плановое задание ежедневно недовыполнялось на 20 ц. Однако в остальные дни бригаде удавалось ежедневно вылавливать на 20 ц больше дневной нормы, и плановое задание было выполнено за 1 день до срока. Сколько центнеров рыбы планировалось вылавливать ежедневно?
этого срока был шторм, вследствие чего плановое задание ежедневно недовыполнялось на 20 ц. Однако в остальные дни бригаде удавалось ежедневно вылавливать на 20 ц больше дневной нормы, и плановое задание было выполнено за 1 день до срока. Сколько центнеров рыбы планировалось вылавливать ежедневно?
Решение:
Допустим, планировалось в течение 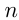 дней ежедневно вылавливать
дней ежедневно вылавливать 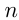 ц рыбы. Тогда:
ц рыбы. Тогда:

Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Решение задач на смеси, процентное содержание и концентрации по математике |
| Решение задач на движение по математике |
| Решение задач на части по математике |
| Решение задач на числа по математике |

