Оглавление:







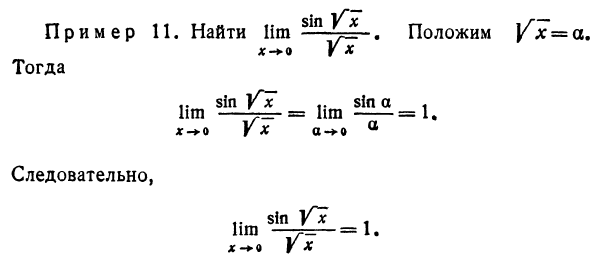



Решение задач на нахождение пределов
- Решить проблему нахождения пределов При решении проблемы определения пределов необходимо помнить некоторые ограничения, чтобы избежать повторного пересчета каждый раз. Объедините эти известные ограничения, чтобы найти новые ограничения, используя свойства, показанные в §4.Пример 12. Найти lim Sin ^ g6 * + 9) х шх + 9 Если аргумент стремится к нулю, установите отношение между синусом и аргументом. Если x2-6 * +9 представлен как, .. грех (я * —6х + 9) грех а. lim- *, Γ = Im- = 1. * 6л; + 9 а 1 cos X Пример 13. Поиск лим.
1 fs’mi- ~ 2 —- lim —— = lim — (- X- * Q X X- + Q * \ 2 я не знаю 1-, 1 = Thm-. lim ——— = -. 1,1 = — * X-U X-yQ L Z 2 2 Пример 14. Найти лим —. Для того, чтобы преобразовать X- * O X Формула: lim = Hsh (/ 4 + 1-2) (^ 4 + ^ + 2) = x —► o x X th x (/ 4 + x + 2) = lim- ^ -‘- lim х (/ 4 + х + 2) * (/ 4 + * + 2) = nga 1 ^ 1 ^ 1 = 1 x- + * V до 4 + x + 2/4 + 7 + 2 2 + 2 4
Введите половину х х Вспоминая угол и предыдущий пример, ободок l-cosx 2 sin> J Людмила Фирмаль
Пример 15. Найти lim e (от X до *) Z и lim х ± <х х ± кп Жим лежа (x — a) 2 = r; (x — a) 2 всегда отрицателен с x и растет бесконечно, поэтому x —►ioo new Переменная z — * oO. Следовательно, см г <* — а> 2 = ± » ? = lim ex = oc (см. замечания в § 5). Z ~> CO Аналогично, lim * — (X-a) a == Um e ~ r = 0 x ± co g-> co — (X-a) 2 бесконечно сокращается при x-> ± oo (см. Замечания в § 5).
Для удобства показаны наиболее распространенные ограничения. ограничение 1 lim x = a х а 2 лим 1 = 0 Используйте X- * + X 3 лим х — я со X ± CD 4 лим -1 = 00 0 1 X 1 5 lim sinx-l X 0 X 6 lim f (x) = f (a) t f (x) непрерывно х а Если вы знаете, что функция непрерывна, вместо определения предела вычислите значение функции. Пример 1. Найти lim (n1-6d: +8).
- Потому что есть много От X до> 2 Термин является непрерывной функцией, lim (* 3-6 * + 8) = 2′-6-2 + 8 = 4. X- + 2 Пример 2. Поиск лим-2- , Найти первым х-х ° х Для знаменателя: lim (x + 5l 🙂 = 1 + 5-1 = 6; он не равен X- + 1 Если ноль, § 4 свойство 4 может быть применено. lim (x * — 2x + 1) x * — 2x + 1 ^ _ lim (x2 + 5x) X — * — 1 Обод 2. и I8—2-1 + 1 _Оп12 + 5-1 до 6 ‘ Пример 3. Нахождение лим LG-V-л 1 Знаменательные ограничения X * + X Свойство 4 в § 4 не применимо, потому что оно равно нулю. Числитель является константой, а знаменатель (x2 + x) — ►O
При x-1 вся дробь бесконечно возрастает по абсолютной величине. То есть лим 1 1 X- * -1 х * — \ — х Пример 4. Поиск лим \ -. Знаменательные ограничения X 2 * — ‘ Равен нулю: lim (x2-6d; +8) = 22-6-2 + 8 = 0, поэтому Свойство 4§4 не применяется. Тем не менее, нет никаких ограничений числителя. lim (x2-5x + 6) = 22-5-2 + 6 = 0. Поэтому предварительно х- + г Задача числителя и знаменателя равна нулю одновременно.
(по теореме Безу). на самом деле x * — 5x + 6 _ (x — 2) (x — 3) _ x — 3 x2-6x + 8- (x — 2) (x-4) ~~ x — 4 ‘ Таким образом, .. —5x + 6 .. x — 3 —1 1 Пример 5. Найти lim xn (n целое, положительное). X s У нас есть n раз Каждый элемент растет бесконечно, поэтому продукт растет бесконечно. lim xn = os. X s = оо
Однако, поскольку число 2 является корнем как числителя, так и знаменателя, дробь можно уменьшить на разность x — 2 Людмила Фирмаль
Пример 6. Найти lim x11 (ri целое, положительное). X -> — 00 xn = X’x … x. Каждый фактор растет по абсолютной величине и остается отрицательным, поэтому, если он четный, произведение растет бесконечно и остается положительным, то есть lim xn = + oo (если n четное). Если порядок нечетный, абсолютное значение товара велико, но остается отрицательным. То есть lim xn = -oo (если n нечетное число). р-у
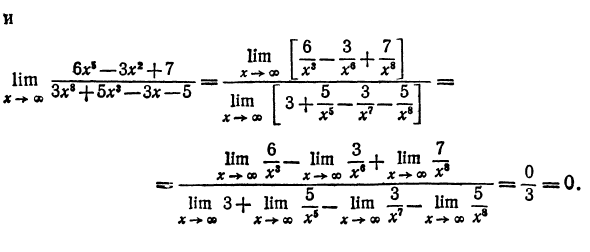
ХТ Пример 7. Поиск лим. х Используйте х — * — л Если m> n, вы можете написать: m = n + kt, где &> 0. так xt xn + k lim- = lim —Mtx. X co * xx x Я пришел к примеру 6. Однако, если /> 0) и ^ t xt I lim -5 = lim -f =% = lim X —► O X- * 00 A X 00 Здесь числитель остается постоянным, а знаменатель растет в абсолютном значении, lim b = 0. X — * — 00 л Мы рекомендуем вам запомнить результаты этого примера в следующем формате: Степенная функция растет быстрее, когда экспоненциальная функция становится больше. Пример 8. Нахождение lim ^ x ^ + ^ -3x ^ -B * ^ 9T0M пример Числитель и знаменатель увеличиваются бесконечно. Разделите числитель и знаменатель на высший порядок х. Итак, х8, 6 3 7 6 * «-3x ‘+ 7 Xs xv + x8 Zx8 + 5×8 — Zx — 5 JL_i__JL «Vs V? V8
и Обод A 3x * + 7 Um 00 — + — 1! limΓX с L 3 + 1 3! Лим 1 — Лим 2+ Лим 1 Лим 3+ Лим Лим 1 — Лим ^ 3 Используйте X o oo X * X F X x-> X x * _7x Пример 9. Найти предел. Сделать преобразование * -gJ Ния, мы получаем 1: х9-7х .. lim * »4-3 8 = 8 ллм 1- Xω * + ^ x- * ®J_4_J ± д: 1 7 3 Так как lim- = 0 и lim-9 = 0, предел знаменателя равен Используйте X- + X X- * X Вены ноль, но молекулярный предел один. Обод 1GGz Ее л • ш Пример 10. Найти lim 2 + fos * * Рассчитать пределы 2 Напомним, что знаменатель cosjc является непрерывной функцией: lim (2-t-cosx) = 2 + cos £ = 2. Тогда я Пример 11. Поиск lim-Set X- + Q Y X тогда .. грех Yx .. грех а. lim- ~ r = ~ = lim- = 1. Ум-а-а-а так Грех ф lim —tr = -1. Vx
Смотрите также:
| Предел lim (1+jc)*. Число e | Скорость |
| Непрерывные функции | Касательная |

