Оглавление:
Сначала идёт подробная теория по функциям, а потом примеры решения задач по функциям.
Функция
Функция 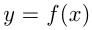 считается заданной, если каждому
считается заданной, если каждому 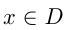 соответствует единственное по определенному правилу вычисленное
соответствует единственное по определенному правилу вычисленное 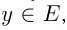 , где
, где 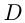 и
и 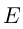 — числовые множества. Говорят, что
— числовые множества. Говорят, что 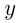 зависит от
зависит от 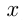 , и функция — это зависимость переменной
, и функция — это зависимость переменной 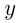 от переменной
от переменной 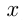 . Множество
. Множество 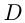 называется областью определения функции, множество
называется областью определения функции, множество 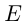 — областью значений функции. Переменную
— областью значений функции. Переменную 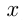 называют независимой переменной, а переменную
называют независимой переменной, а переменную 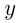 — зависимой. Переменная
— зависимой. Переменная 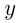 является функцией от
является функцией от 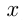 , что записывается
, что записывается 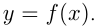 Для записи функций используются и другие буквы:
Для записи функций используются и другие буквы: 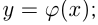
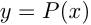 и т. п.
и т. п.
Переменная 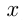 называется аргументом функции,
называется аргументом функции, 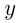 — ее значением.
— ее значением.
Функция может быть задана формулой, таблицей и другими способами. Если функция задана формулой, и область определения функции не указана, то считается, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.
Например, если 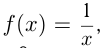 то область определения функции все
то область определения функции все 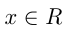 , кроме
, кроме 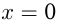 , т. е.
, т. е. 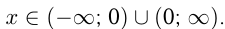
Если 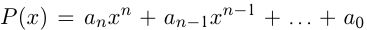 — многочлен, то
— многочлен, то 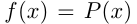 называется целой рациональной функцией; если
называется целой рациональной функцией; если 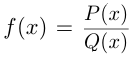 — это дробно-рациональная функция. Например,
— это дробно-рациональная функция. Например, 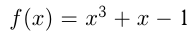 — целая рациональная функция 3-й степени;
— целая рациональная функция 3-й степени; 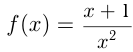 —— дробно-рациональная функция.
—— дробно-рациональная функция.
Введем понятие координатной плоскости. Проведем на плоскости через точку 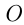 две взаимно перпендикулярных прямые
две взаимно перпендикулярных прямые 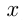 и
и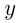 — оси координат. Ось
— оси координат. Ось 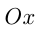 называется осью абсцисс, ось
называется осью абсцисс, ось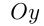 — осью ординат, точка
— осью ординат, точка 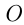 — началом координат. Этой точкой каждая из осей разбивается на две полуоси, одна из которых — положительная, другая — отрицательная.
— началом координат. Этой точкой каждая из осей разбивается на две полуоси, одна из которых — положительная, другая — отрицательная.
Каждой точке плоскости ставится в соответствие пара чисел 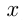 ;
; 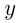 — координаты точки. Это записывается
— координаты точки. Это записывается 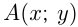 ,
, 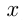 — абсцисса точки,
— абсцисса точки, 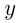 — ордината. Значение
— ордината. Значение 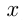 определяется как расстояние от начала координат до основания перпендикуляра, опущенного из точки
определяется как расстояние от начала координат до основания перпендикуляра, опущенного из точки 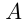 на ось
на ось 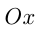 ; значение
; значение 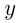 — расстояние от начала координат до основания перпендикуляра, опущенного из точки
— расстояние от начала координат до основания перпендикуляра, опущенного из точки 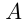 на
на 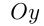 .Для определения значений
.Для определения значений 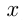 и
и 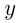 на осях выбираются единичные отрезки.
на осях выбираются единичные отрезки.
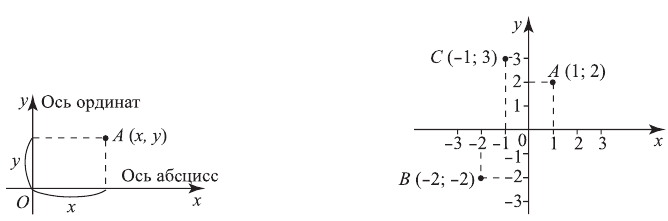
Оси координат разбивают плоскость на 4 четверти: I, II, III и IV. В I четверти обе координаты положительны, во II — координата 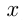 отрицательна,
отрицательна, 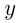 положительна, в III — обе координаты отрицательны, в IV —
положительна, в III — обе координаты отрицательны, в IV — 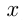 положительна,
положительна, 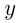 отрицательна. Приведенное описание — это прямоугольная декартова система координат. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. График представляет собой линию на плоскости, непрерывную или разрывную.
отрицательна. Приведенное описание — это прямоугольная декартова система координат. Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции. График представляет собой линию на плоскости, непрерывную или разрывную.
Линейная функция
Функция вида 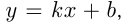 где
где 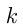 и
и 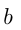 — числа, называется линейной функцией, ее область определения
— числа, называется линейной функцией, ее область определения 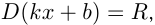 т.е.
т.е. 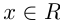 . Область значений линейной функции
. Область значений линейной функции 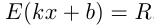 , т. е.
, т. е.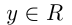 , если
, если 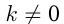 ; если
; если 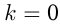 , то
, то 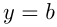 .
.
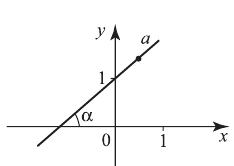
График линейной функции — прямая линия, угол наклона которой к оси 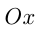 определяется числом
определяется числом 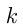 (угловой коэффициент). Если
(угловой коэффициент). Если 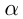 — угол наклона, то
— угол наклона, то 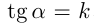 если
если 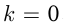 , то прямая параллельна
, то прямая параллельна 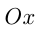 .
.
Например, график функции 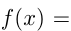
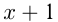 — прямая
— прямая 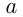 .
.
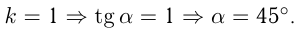
График линейной функции строится по двум точкам, т. к. две точки определяют прямую единственным образом.
Квадратичная функция
Функция 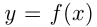 , где
, где 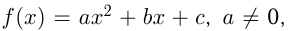 называется квадратичной. Область определения квадратичной функции
называется квадратичной. Область определения квадратичной функции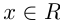 , или
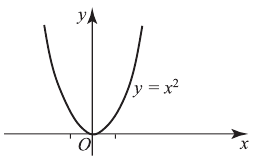
, или 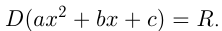 График квадратичной функции называется параболой, ее ветви направлены вверх, если
График квадратичной функции называется параболой, ее ветви направлены вверх, если 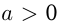 , и вниз, если
, и вниз, если 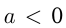 . И в том, и в другом случае парабола имеет вершину, координаты которой вычисляются по следующим формулам:
. И в том, и в другом случае парабола имеет вершину, координаты которой вычисляются по следующим формулам: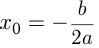 ;
;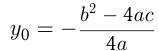 . Обычно при необходимости по формуле вычисляют
. Обычно при необходимости по формуле вычисляют 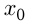 , a
, a 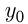 получают подстановкой
получают подстановкой 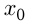 в формулу
в формулу 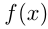 , т. е.
, т. е. 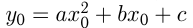 . Парабола имеет вертикальную ось симметрии, проходящую через вершину. Построение параболы часто сводится к нахождению точек пересечения графика с
. Парабола имеет вертикальную ось симметрии, проходящую через вершину. Построение параболы часто сводится к нахождению точек пересечения графика с 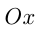 т.е. корней уравнения
т.е. корней уравнения 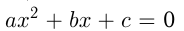 , если они существуют, и координат вершины. Если корней нет, то находят еще несколько точек.
, если они существуют, и координат вершины. Если корней нет, то находят еще несколько точек.
Например, график функции 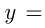
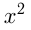 имеет вершину в т.
имеет вершину в т. 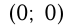 , т.к.
, т.к. 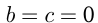 и проходит через точки
и проходит через точки 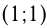 и
и 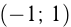 . Построим графики функций
. Построим графики функций 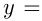
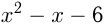 и
и 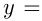
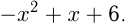
1) 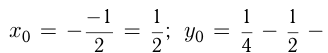
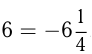
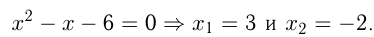
2)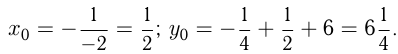 Корни уравнения те же
Корни уравнения те же
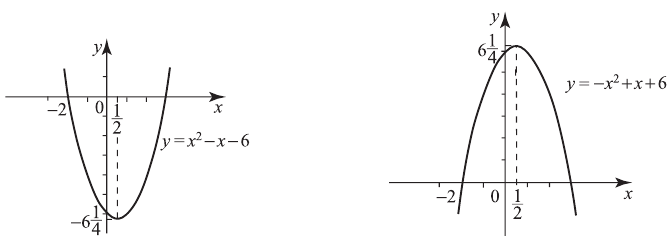
Из графиков видно, что множество значений квадратичной функции 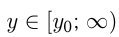 , если
, если 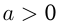 , и
, и 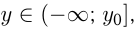 если
если 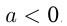
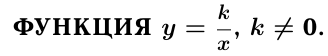
Эта функция называется обратной пропорциональностью. Область ее определения 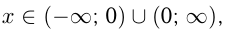 т. к.
т. к. 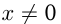 .
.
Множество значений 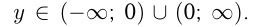 График этой функции называется гиперболой;
График этой функции называется гиперболой;
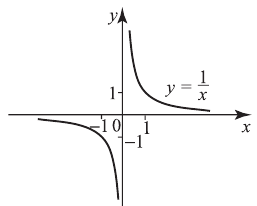
он не имеет точек пересечения с осями 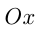 и
и 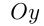 и имеет эти оси в качестве асимптот, т. е. прямых, к которым кривая бесконечно приближается.
и имеет эти оси в качестве асимптот, т. е. прямых, к которым кривая бесконечно приближается.
График расположен в I и III четвертях, если 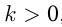 и во II и IV четвертях, если
и во II и IV четвертях, если 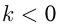 .
.
Например, построим график 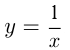 . Он проходит через точки
. Он проходит через точки 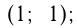
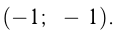 График симметричен относительно начала координат.
График симметричен относительно начала координат.
Степенная функция с целым показателем
Степенной функцией с целым показателем называется функция вида 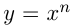 , где
, где 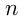 — целое число. Отметим, что частными случаями такой степенной функции являются линейная функция
— целое число. Отметим, что частными случаями такой степенной функции являются линейная функция 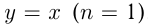 , квадратичная функция
, квадратичная функция 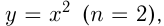 обратная пропорциональность
обратная пропорциональность 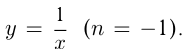 Графики этих функций представлены ниже.
Графики этих функций представлены ниже.
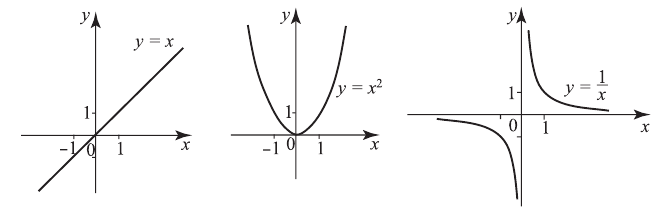
1) Показатель степени 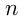 — нечетное положительное число
— нечетное положительное число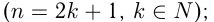
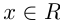 ,
, 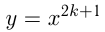 например,
например, 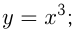
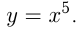
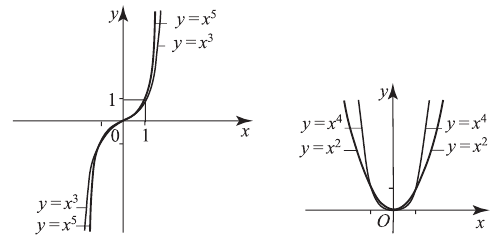
График 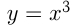 называется кубической параболой.
называется кубической параболой.
2) 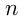 — четное положительное число
— четное положительное число 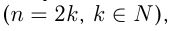
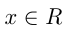 .
.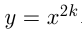 , например,
, например, 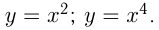
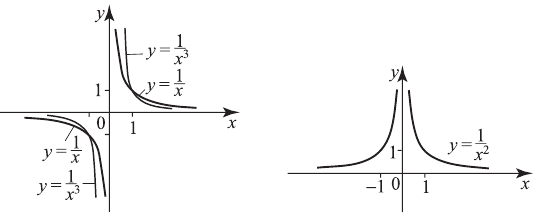
3) 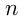 — нечетное отрицательное число
— нечетное отрицательное число 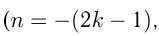
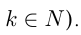
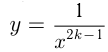 например,
например, 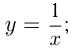
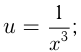
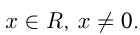
4) 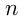 — четное отрицательное число
— четное отрицательное число 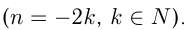
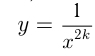 например ,
например , 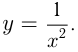
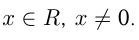
Показательная функция
Функция 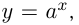 где
где 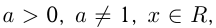 называется показательной. При этом
называется показательной. При этом 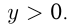 Функция имеет различные графики при
Функция имеет различные графики при 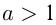 и
и 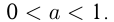
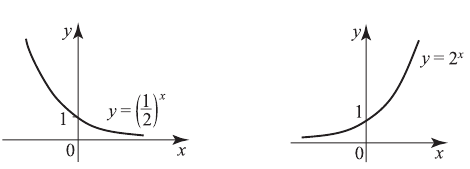
1) 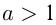 ; если
; если 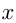 возрастает, то
возрастает, то 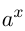 также возрастает, например,
также возрастает, например, 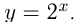
2) 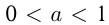 ; если
; если 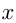 возрастает, то
возрастает, то 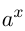 убывает, например,
убывает, например, 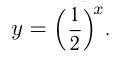
Логарифмическая функция
Функция 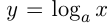 , где
, где 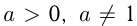 и
и 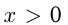 , называется логарифмической. Так же, как и в случае показательной функции, существуют 2 графика логарифмической функции: при
, называется логарифмической. Так же, как и в случае показательной функции, существуют 2 графика логарифмической функции: при 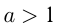 и при
и при 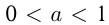 . Например,
. Например, 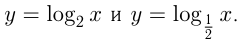
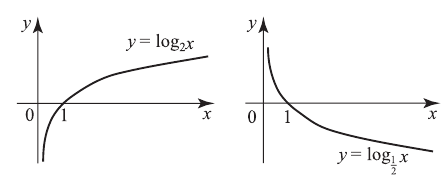
Тригонометрические функции
Тригонометрическими функциями называются функции 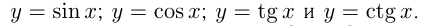
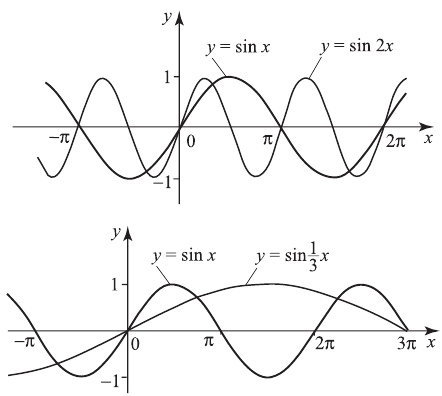
1) 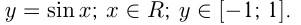 График — синусоида, период
График — синусоида, период 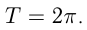
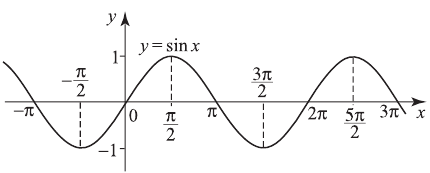
2) 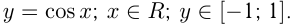 График — синусоида, период
График — синусоида, период 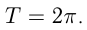
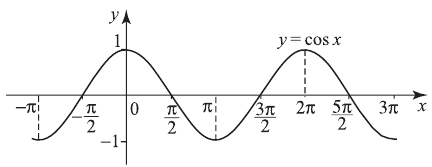
3) 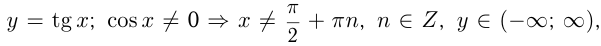 период
период 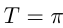
4) 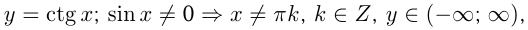 период
период 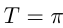 .
.
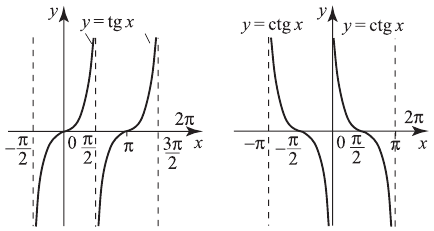
Функции: 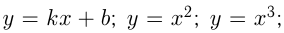
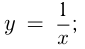
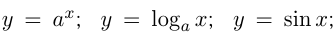
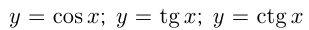 относятся к элементарным. К ним присоединяют еще
относятся к элементарным. К ним присоединяют еще 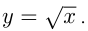
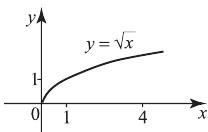
График функции 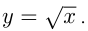
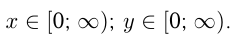
Преобразование графиков функции
Одним из способов построения графиков является способ получения из графика функции 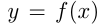 графиков функций следующего вида:
графиков функций следующего вида:
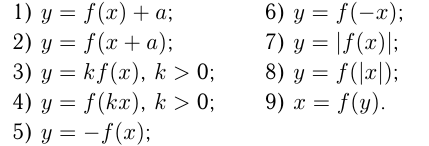
Построение нового графика происходит на основе графика элементарной функции путем его преобразования.
В 1-м случае график 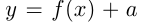 получается из графика
получается из графика 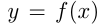 путем сдвига этого графика как единого целого вдоль оси ординат на
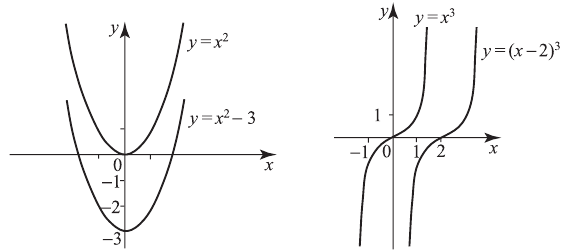
путем сдвига этого графика как единого целого вдоль оси ординат на 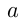 единиц. Например, построим график функции
единиц. Например, построим график функции 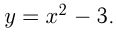 Сначала построим график
Сначала построим график 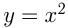 и затем сдвинем его на 3 единицы вниз.
и затем сдвинем его на 3 единицы вниз.
Во 2-м случае график 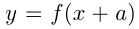 получается из графика
получается из графика 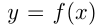 путем сдвига вдоль оси абсцисс на
путем сдвига вдоль оси абсцисс на 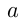 единиц влево, если
единиц влево, если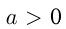 , и вправо, если
, и вправо, если 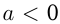 . Например, построим график
. Например, построим график 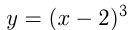
В 3-м случае для построения графика 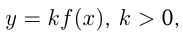 надо растянуть график
надо растянуть график 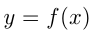 в
в 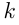 раз вдоль оси ординат при неиз —
раз вдоль оси ординат при неиз —
менной оси абсцисс. Если 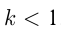 , то растяжение часто называют сжатием. Например, построим графики:
, то растяжение часто называют сжатием. Например, построим графики: 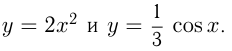
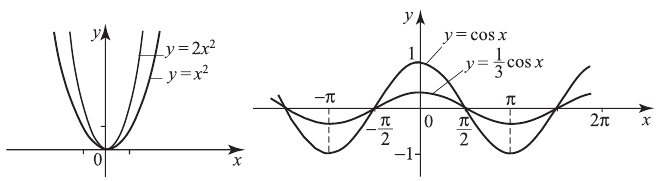
В 4-м случае для построения графика 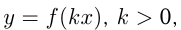 надо растянуть или сжать вдоль оси абсцисс при неизменной оси ординат график
надо растянуть или сжать вдоль оси абсцисс при неизменной оси ординат график 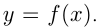 Если
Если 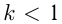 , происходит растяжение, если
, происходит растяжение, если 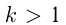 — сжатие. Например, построим графики
— сжатие. Например, построим графики 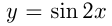 и
и 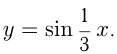
В 5-м случае для получения графика 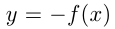 из графика
из графика 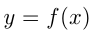 нужно отразить его симметрично относительно оси абсцисс. Например, построим график функции
нужно отразить его симметрично относительно оси абсцисс. Например, построим график функции 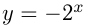 .
.
В 6-м случае для получения графика 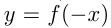 из графика
из графика 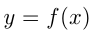 нужно отразить его симметрично относительно оси ординат. Например, построим график функции
нужно отразить его симметрично относительно оси ординат. Например, построим график функции 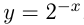 .
.
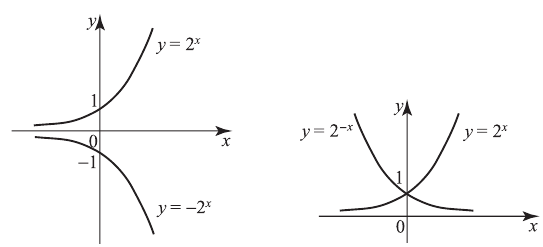
В 7-м случае для получения графика 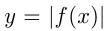 из графика
из графика 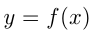 нужно отразить симметрично относительно оси абсцисс часть графика, лежащую ниже этой оси. Например, построим график
нужно отразить симметрично относительно оси абсцисс часть графика, лежащую ниже этой оси. Например, построим график 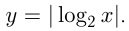
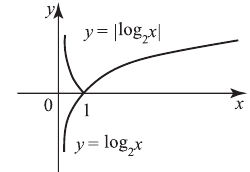
В 8-м случае для получения графика 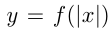 из графика
из графика 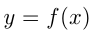 нужно заменить часть графика, лежащую слева от оси ординат, графиком, симметричным части графика, лежащей справа от оси ординат. Например, построим график
нужно заменить часть графика, лежащую слева от оси ординат, графиком, симметричным части графика, лежащей справа от оси ординат. Например, построим график 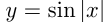
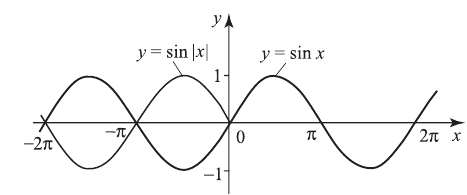
9-й случай — это получение обратной функции. Такими взаимно обратными функциями являются 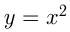 и
и 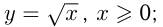
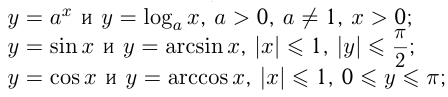
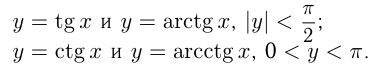
Для построения обратной функции нужно функцию 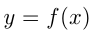 симметрично отразить относительно биссектрисы прямого угла I четверти координатной плоскости. Например, графики
симметрично отразить относительно биссектрисы прямого угла I четверти координатной плоскости. Например, графики 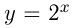 и
и 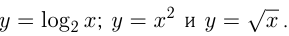
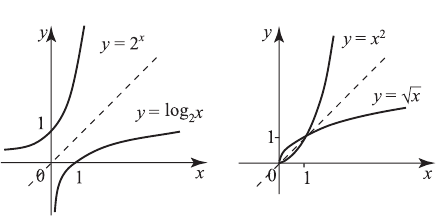
Свойства функций
1) Четность. Функция 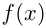 называется четной, если на всей области определения
называется четной, если на всей области определения 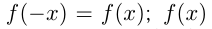 называется нечетной, если на всей области определения
называется нечетной, если на всей области определения 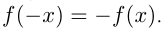 Например,
Например,
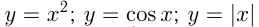 — четные функции.
— четные функции.
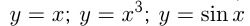 — нечетные функции.
— нечетные функции.
График четной функции симметричен относительно оси ординат; график нечетной функции симметричен относительно начала координат.
2) Периодичность. Функция 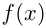 называется периодической, если на всей области определения
называется периодической, если на всей области определения 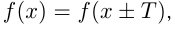 где
где 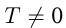 — период.
— период.
Например, функции 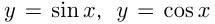 — периодические с периодом
— периодические с периодом 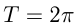 ; функции
; функции 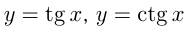 — периодичес-кие с периодом
— периодичес-кие с периодом 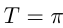 . Период функции
. Период функции 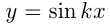 равен
равен 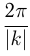 , аналогично для
, аналогично для 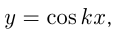
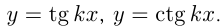
3) Возрастание. Функция 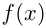 возрастает на некотором интервале из области определения, если для любых
возрастает на некотором интервале из области определения, если для любых 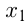 и
и 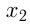 из этого интервала таких, что
из этого интервала таких, что 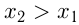 , выполняется
, выполняется 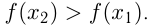
4) Убывание. Функция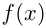 убывает на некотором интервале из области определения, если для любых
убывает на некотором интервале из области определения, если для любых 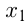 и
и 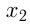 из этого интервала таких, что
из этого интервала таких, что 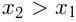 выполняется
выполняется 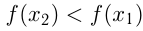 .
.
5) Экстремумы. Точка 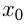 называется точкой минимума функции
называется точкой минимума функции 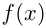 , если для всех
, если для всех 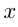 из некоторой окрестности
из некоторой окрестности 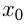 выполняется
выполняется 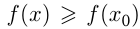 . Само значение
. Само значение 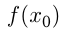 — минимум функции (min). Точка
— минимум функции (min). Точка 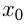 называется точкой максимума функции
называется точкой максимума функции 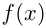 , если для всех
, если для всех 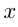 из некоторой окрестности
из некоторой окрестности 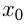 выполняется
выполняется 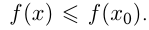 Само значение
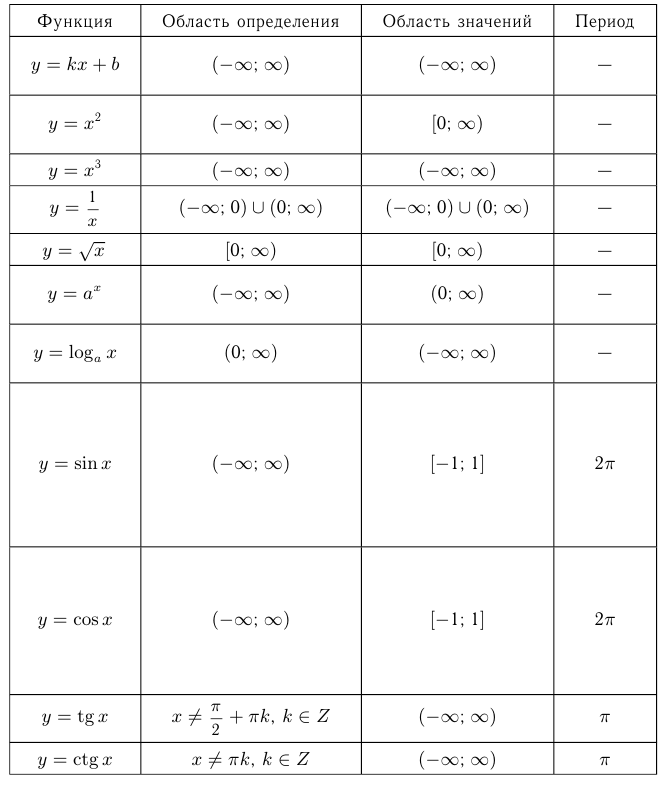
Само значение 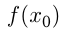 в этом случае называется максимумом функции (max). Выше приведена таблица свойств элементарных функций.
в этом случае называется максимумом функции (max). Выше приведена таблица свойств элементарных функций.

Производная функции
Допустим, областью определения функции 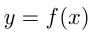 является интервал
является интервал 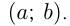 Возьмем точку
Возьмем точку 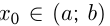 и точку
и точку 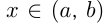 в окрестности точки
в окрестности точки 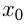 ; тогда разность
; тогда разность 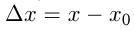 называется приращением аргумента в точке
называется приращением аргумента в точке 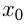 .
.
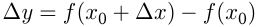 — приращение функции в точке
— приращение функции в точке 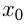 .
.
Число 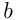 называется пределом функции
называется пределом функции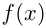 в точке
в точке 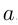 , если для любого
, если для любого 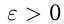 при всех
при всех 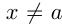 , достаточно близких к
, достаточно близких к 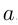 , выполняется неравенство
, выполняется неравенство  . Обозначается
. Обозначается 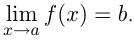
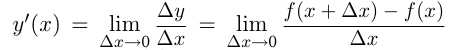
производная функции 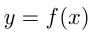 равна пределу отношения приращения функции к приращению аргумента, если такой предел существует и конечен. Производная функции
равна пределу отношения приращения функции к приращению аргумента, если такой предел существует и конечен. Производная функции 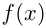 также обозначается
также обозначается 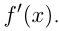
Производные элементарных функций
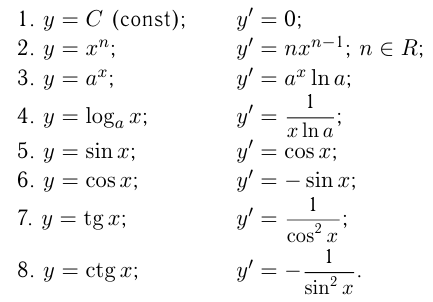
Правила вычисления производных
Если для функций 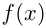 и
и 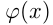 существуют производные
существуют производные 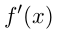 и
и 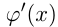 , то:
, то:
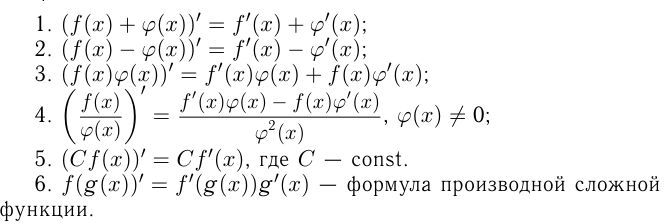
Если функция имеет производную на некотором интервале, то она называется дифференцируемой на этом интервале.
Если в каждой точке интервала 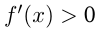 , то
, то 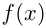 возрастает на этом интервале.
возрастает на этом интервале.
Если в каждой точке интервала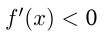 , то на этом интервале
, то на этом интервале 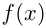 убывает.
убывает.
Если на интервале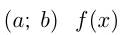 имеет производную
имеет производную 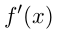 и
и 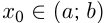 и если
и если 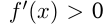 при
при 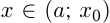 и
и 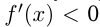 при
при 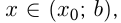 то точка
то точка 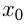 является точкой максимума функции
является точкой максимума функции 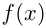 ; при этом
; при этом 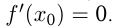
И наоборот, если при тех же условиях 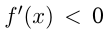 при
при 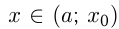 и
и 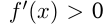 при
при 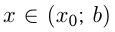 , то точка
, то точка 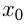 — точка минимума функции
— точка минимума функции 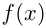 , при этом
, при этом 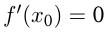 .
.
Уравнение касательной к графику функции
Касательная к графику 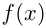 в точке
в точке 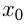 , если
, если 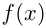 дифференци-руема в точке
дифференци-руема в точке 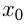 , — это прямая, проходящая через точку
, — это прямая, проходящая через точку 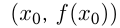 и имеющая угловой коэффициент
и имеющая угловой коэффициент 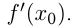 Уравнение касательной:
Уравнение касательной: 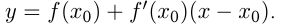
Например, напишем уравнение касательной к функции 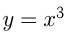 в точке
в точке 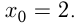
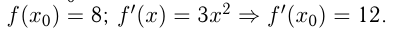
Уравнение касательной: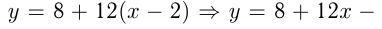
Исследование функций и построение графиков
Исследование функции, т.е. наиболее полное описание ее свойств, производится, как правило, для построения ее графика и состоит из нескольких пунктов:
- область определения функции;
- область значений функции;
- четность, нечетность функции;
- периодичность функции;
- определение нулей функции, т.е. значений
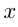 , в которых функция обращается нуль, и значения
, в которых функция обращается нуль, и значения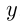 , которое принимает функция при
, которое принимает функция при 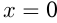 ;
; - интервалы возрастания и убывания функции;
- экстремумы функции;
- нахождение, если это необходимо, дополнительных точек для построения графика.
Иногда к перечисленным пунктам добавляют еще нахождение интервалов знакопостоянства функции.
Однако для построения графика не всегда бывает необходимо проводить исследование по полной схеме, достаточно тех пунктов, которые дают возможность построить график. Так, бывает трудно найти область значений функции и нули функции.
Пример. Исследовать функцию и построить ее график.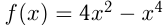 .
.
1.Область определения 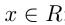 .
.
3.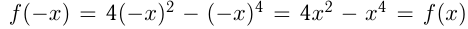 функция четная.
функция четная.
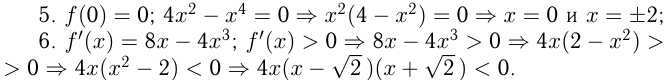
Метод интервалов:
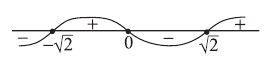
Функция возрастает на интервалах: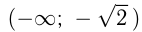 и
и 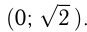
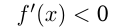 при
при 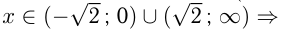 на этих интервалах функция убывает.
на этих интервалах функция убывает.
7.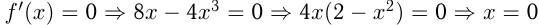 и
и 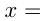
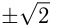 — эти значения
— эти значения 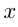 называют критическими точками.
называют критическими точками.
Только там, где 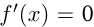 , возможны экстремумы функции. Экстремумы легко определить по схеме.
, возможны экстремумы функции. Экстремумы легко определить по схеме.
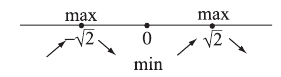
Стрелка, направленная вверх, означает возрастание функции, вниз — убывание.
Если в критической точке возрастание функции сменяется убыванием, то в этой точке — максимум, если наоборот — минимум.
8.Составим небольшую таблицу:

Строим график. Область значений функции, которую сразу определять было сложно, 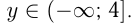
Наибольшее и наименьшее значения функции
Решение многих практических задач часто сводится к нахождению наибольшего и наименьшего значений непрерывной на отрезке функции. Правило нахождения этих значений таково: чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек, нужно вычислить значения функции во всех критических точках и на концах отрезка, а затем из полученных чисел выбрать наибольшее и наименьшее.
Например, найдем наименьшее и наибольшее значения функции 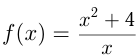 на отрезке
на отрезке 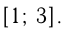
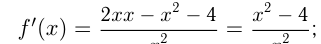
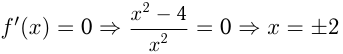 критические точки.
критические точки.
Составим таблицу: 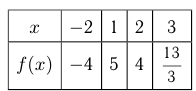
Итак, наименьшее значение 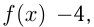 а наибольшее 5, часто это записывают так:
а наибольшее 5, часто это записывают так: 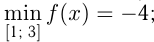
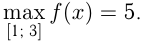
Первообразная и интеграл
Функция 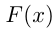 называется первообразной для функции
называется первообразной для функции 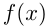 на некотором промежутке, если для всех
на некотором промежутке, если для всех 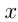 из этого промежутка
из этого промежутка
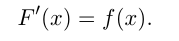
Например, функция 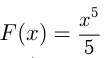 -первообразная для функции
-первообразная для функции 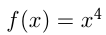 при
при 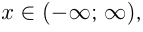 так как
так как
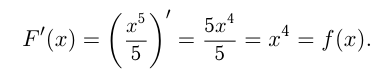
Любая первообразная для 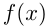 при
при 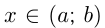 может быть записана как
может быть записана как 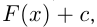 где
где 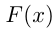 — одна из первообразных для
— одна из первообразных для 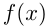 при
при 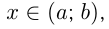 а
а 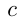 — произвольное число.
— произвольное число.
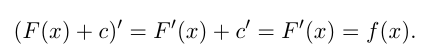
Нахождение первообразной для функции — действие, обратное нахождению производной. Исходя из этого, можно составить таблицу первообразных некоторых функций.
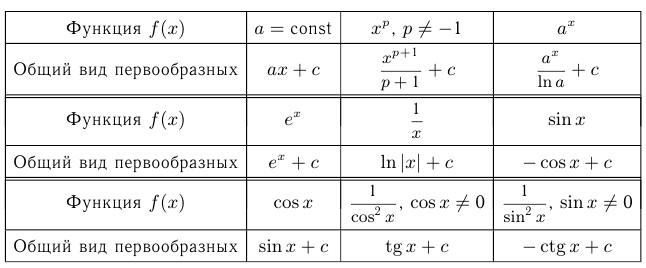
Три правила нахождения первообразных
- Если
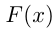 — первообразная для
— первообразная для 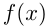 , a
, a 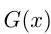 — первообразная для
— первообразная для 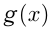 , то
, то 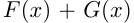 — первообразная для
— первообразная для 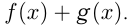
- Если
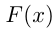 — первообразная для
— первообразная для 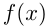 и
и 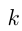 — число, то
— число, то 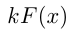 — первообразная для
— первообразная для 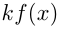 .
. - Если
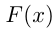 — первообразная для
— первообразная для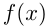 ,
, 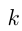 и
и 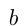 — числа и
— числа и 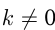 , то
, то 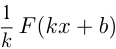 — первообразная для
— первообразная для 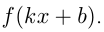
Например, найдем первообразные.
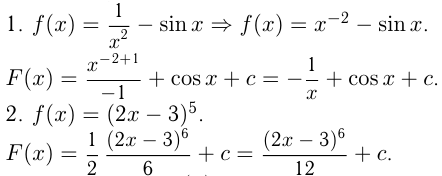
Пусть функция 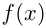 непрерывна на отрезке
непрерывна на отрезке 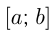 и не меняет знака на этом отрезке. Тогда фигуру, ограниченную графиком этой функции, отрезком
и не меняет знака на этом отрезке. Тогда фигуру, ограниченную графиком этой функции, отрезком 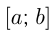 и прямыми
и прямыми 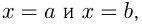 называют криволинейной трапецией.
называют криволинейной трапецией.
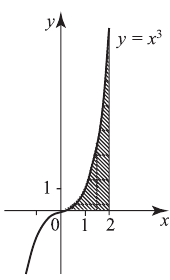
Например, 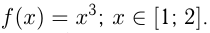
Заштрихованная фигура — криволинейная трапеция.
Для вычисления площади криволинейной трапеции применяется формула:
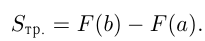
В нашем примере 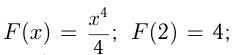
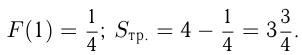
Площадь криволинейной трапеции может быть получена так же, как 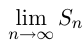 где
где 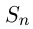 — сумма площадей
— сумма площадей 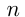 прямоугольников, на которые разбивается криволинейная трапеция. Основания прямоугольников
прямоугольников, на которые разбивается криволинейная трапеция. Основания прямоугольников 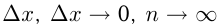 и
и 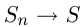 (площадь трапеции). Суммирование площадей называется интегрированием, а площадь трапеции выражается как интеграл, т.е.
(площадь трапеции). Суммирование площадей называется интегрированием, а площадь трапеции выражается как интеграл, т.е.
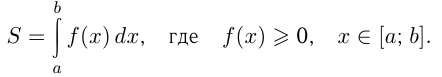
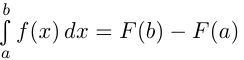 — формула Ньютона-Лейбница.
— формула Ньютона-Лейбница.
Для удобства используют запись:
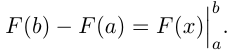
Например, 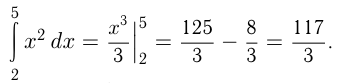
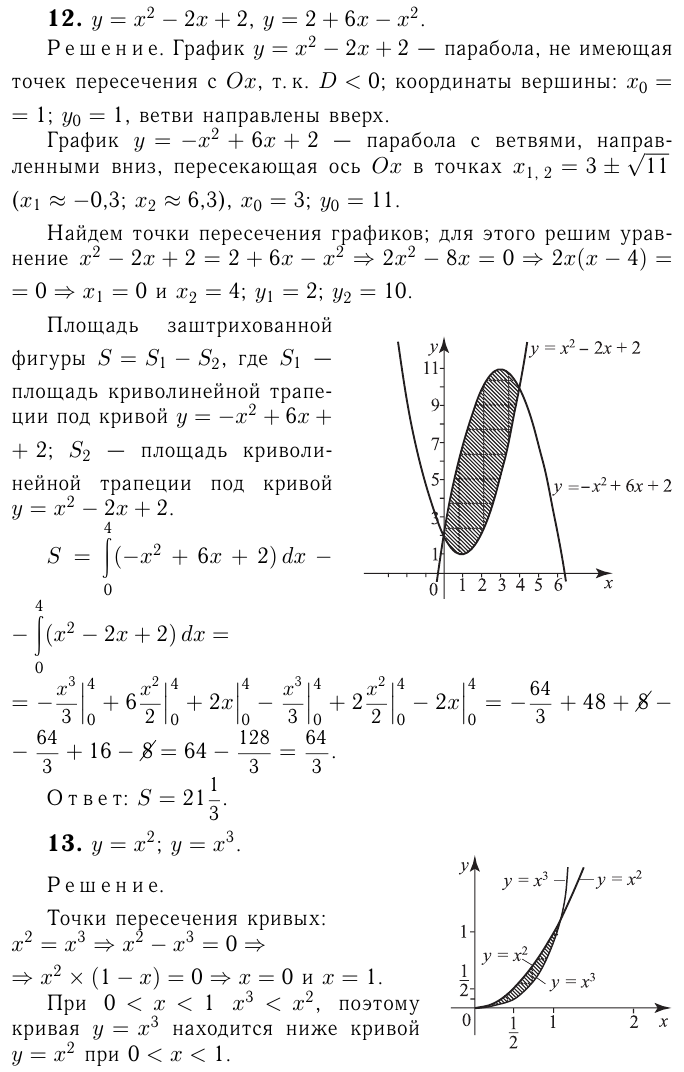
Вычислим площадь фигуры, ограниченной линиями: 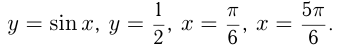
Сделаем чертеж.
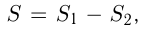 где
где 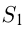 — площадь криволинейной трапеции,
— площадь криволинейной трапеции,
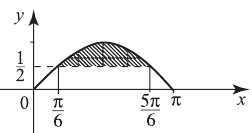
ограниченной синусоидой, осью 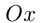 и прямыми
и прямыми 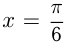 и
и 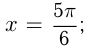
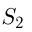 — площадь 6 6 прямоугольника, ограниченного прямыми
— площадь 6 6 прямоугольника, ограниченного прямыми 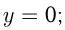
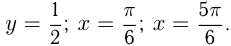
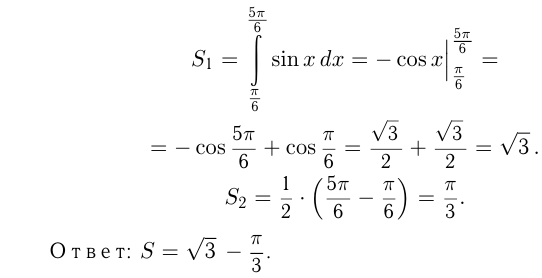
Решение задач на функции
Найти область определения функций



Найти область значений функции
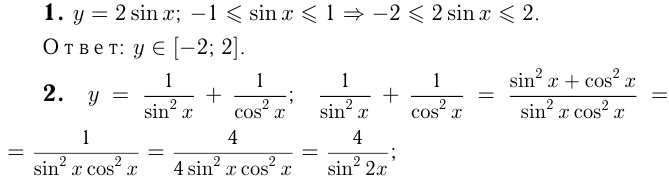
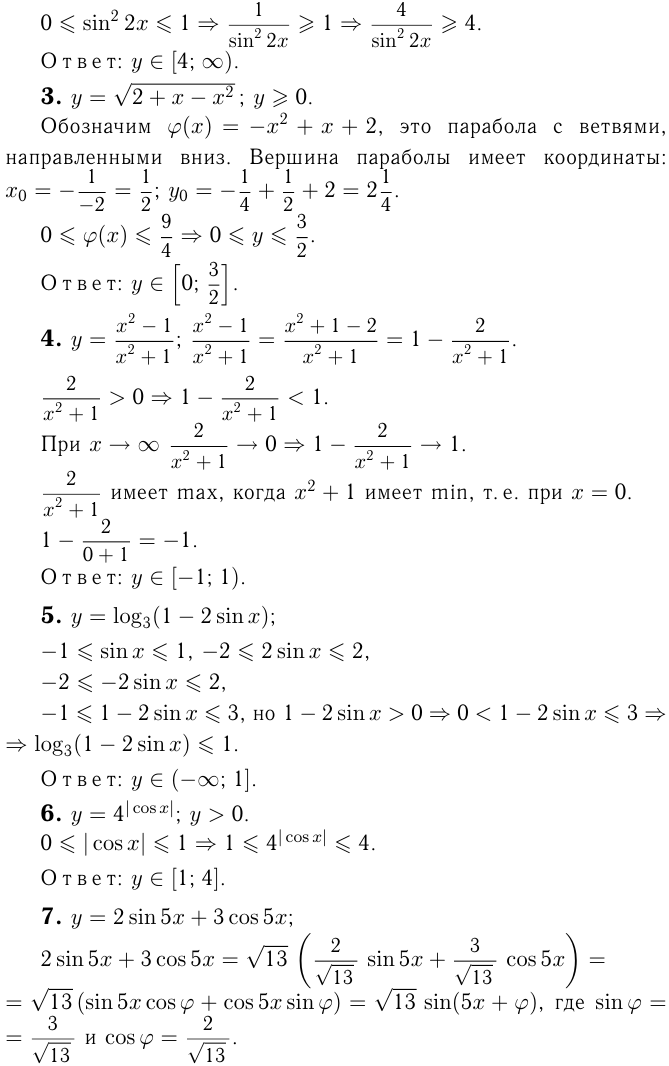

Построить график функций методом преобразования
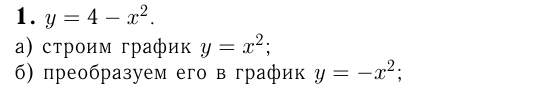
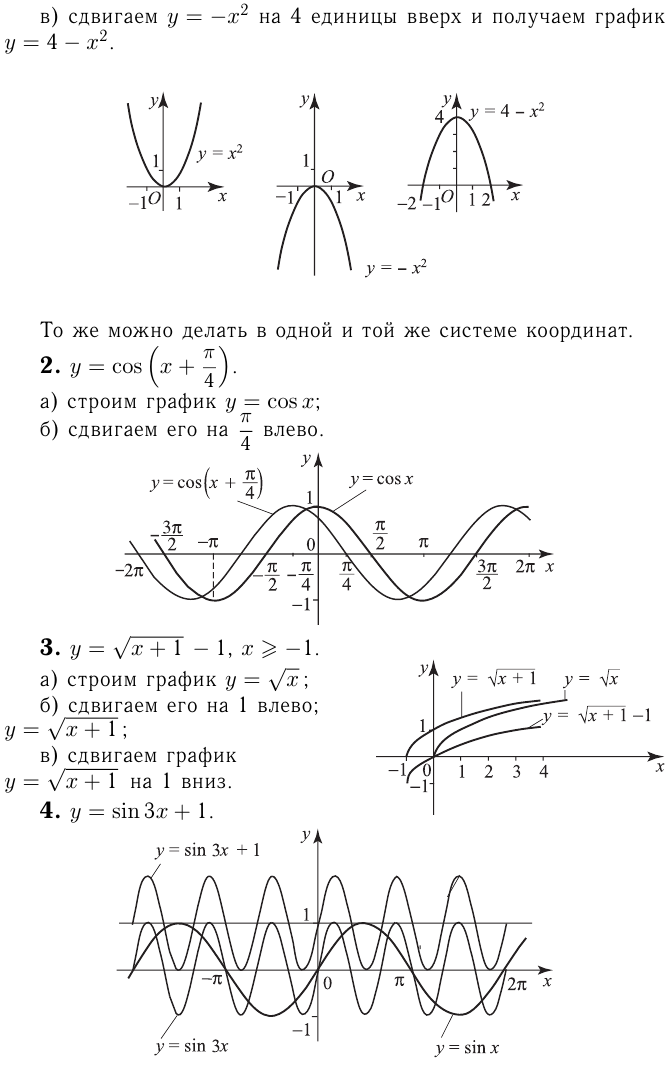
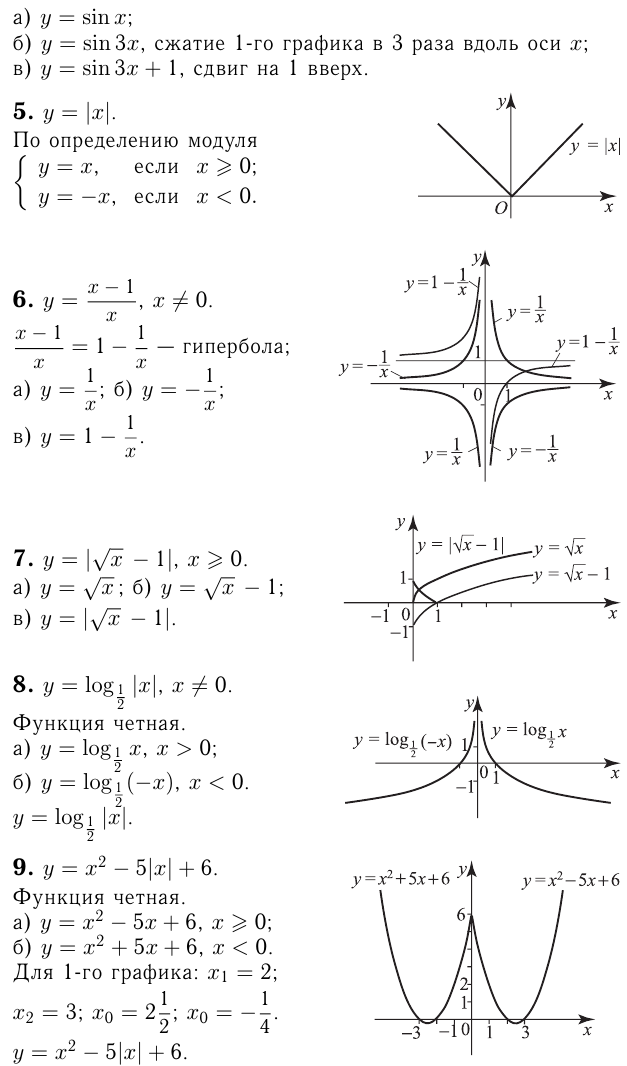
Какие из следующих функций являются чётными? нечётными? не являются ни чётными, ни нечётными?

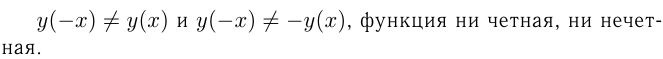
Определить период функций

Найти производные функций
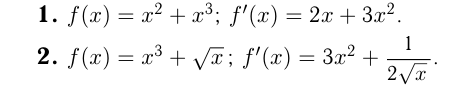

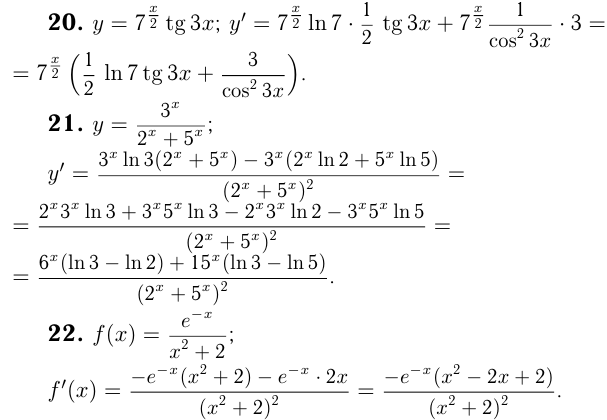
Касательная к графику функции
Задача №160
Написать уравнение касательной к графику функции в точке 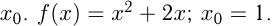
Решение, 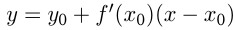 — уравнение касательной, где
— уравнение касательной, где 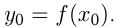
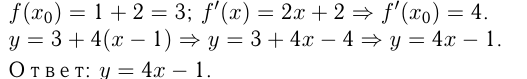
Задача №161
Найти тангенс ума наклона касательной, проходящей через точку 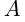 графика функции
графика функции 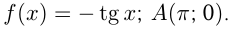
Решение:
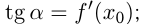
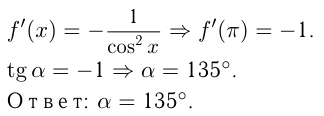
Задача №162
Написать уравнение касательной к графику функции 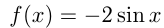 в точке
в точке 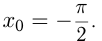
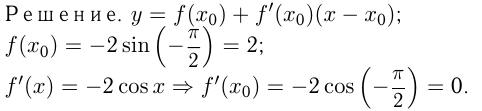
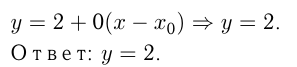
Задача №163
Найти точки графика функции 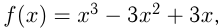 в которых касательная параллельна оси абсцисс.
в которых касательная параллельна оси абсцисс.
Решение:
Если прямая 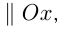 , то угол между ними равен
, то угол между ними равен 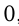 , т. е.
, т. е.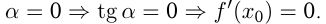
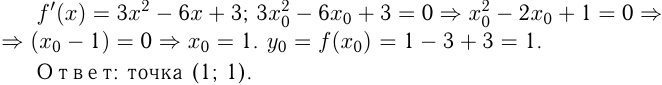
Задача №164
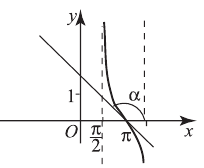
Под каким углом пересекается с осью 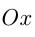 график функции
график функции 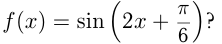
Решение:
Угол пересечения определяется углом между касательной к графику в точке пересечения и осью 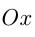 .
.
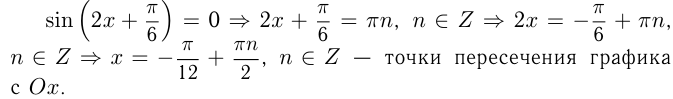
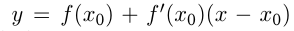 — уравнение касательной, где
— уравнение касательной, где 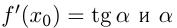 — угол наклона касательной к
— угол наклона касательной к 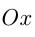 в точке
в точке 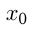 .
.
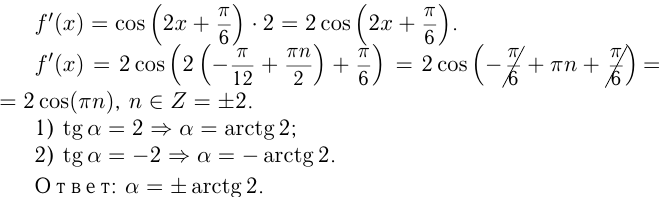
Задача №165
Под каким углом пересекается с осью 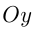 график функции
график функции 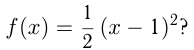
Решение. График пересекается с 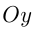 в точке
в точке 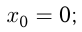
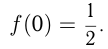
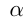 — угол наклона касательной в точке
— угол наклона касательной в точке 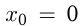 к
к 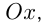
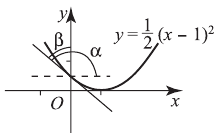
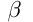 — угол наклона касательной в этой же точке к
— угол наклона касательной в этой же точке к 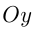 ;
;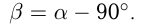
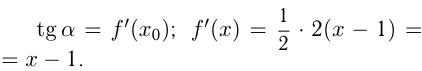
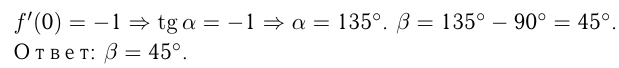
Задача №166
Найти все значения 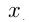 , при которых касательные к графикам функций
, при которых касательные к графикам функций 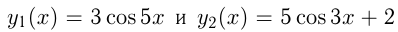 в точках с абсциссой
в точках с абсциссой 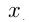 параллельны.
параллельны.
Решение:
Параллельность касательных означает равенство их угловых коэффициентов. Поэтому 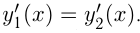
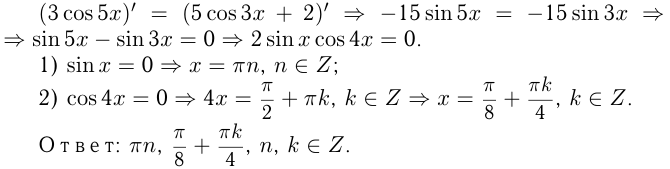
Задача №167
К параболе 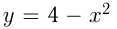 в точке с абсциссой
в точке с абсциссой 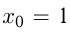 проведена касательная. Найти точку пересечения этой касательной с
проведена касательная. Найти точку пересечения этой касательной с 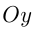 .
.
Решение:
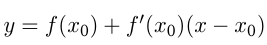 — уравнение касательной.
— уравнение касательной.
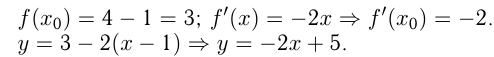
При пересечении с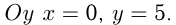
Ответ: точка 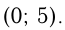
Задача №168
Найти координаты точки пересечения двух касательных, проведенных к графику функции 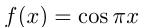 в точке с абсциссой
в точке с абсциссой 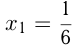 и в точке с абсциссой
и в точке с абсциссой 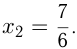
Решение:
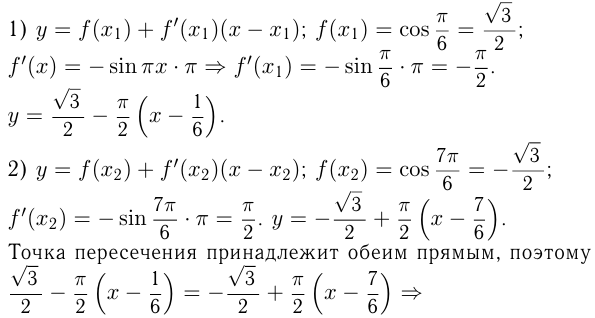
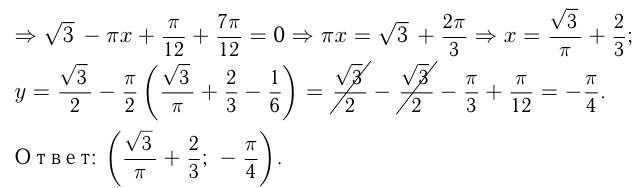
Задача №169
Найти уравнения общих касательных к параболам 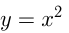 и
и 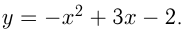
Решение:
1) Касательная к 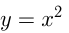 проходит через точку с абсциссой
проходит через точку с абсциссой 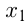 этой параболы. Уравнение касательной:
этой параболы. Уравнение касательной: 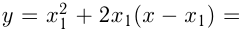
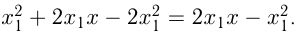
2) Касательная к 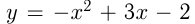 проходит через точку с абсциссой
проходит через точку с абсциссой 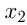 этой параболы. Уравнение касательной:
этой параболы. Уравнение касательной:
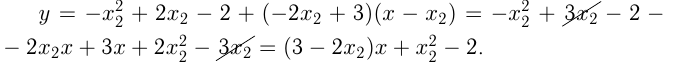
Эти касательные — одна и та же прямая, следовательно их угловые коэффициенты и свободные члены совпадают.
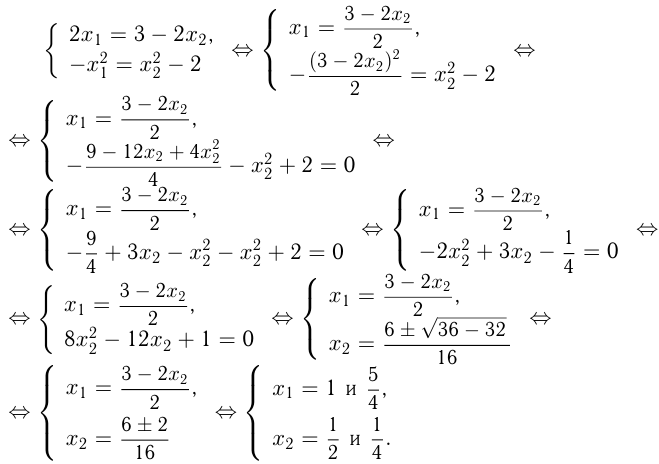
Уравнения касательной к функции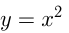 в точке с абсциссой
в точке с абсциссой
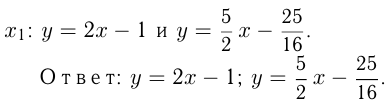
Задача №170
Вычислите площадь треугольника, ограниченного осями координат и касательной к графику функции 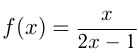 в точке с абсциссой
в точке с абсциссой 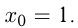
Решение:
Сделаем схематический чертеж. Функция 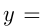
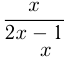 гипербола, т. к.
гипербола, т. к.
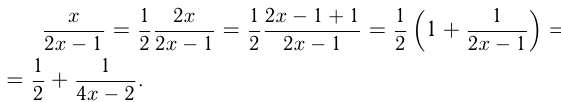
Эта гипербола имеет асимптоты 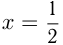 и
и 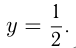 Т. к.
Т. к. 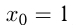 , начертим только одну ветвь гиперболы.
, начертим только одну ветвь гиперболы.
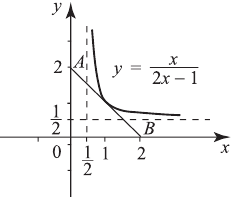
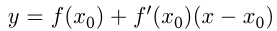 — Уравнение касательной.
— Уравнение касательной.
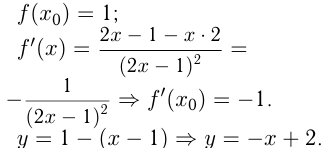
Эта прямая пересекается с 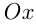 при
при 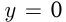 в точке
в точке 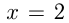 и пересекается с
и пересекается с 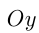 при
при 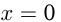 в точке
в точке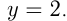
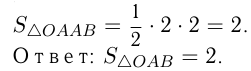
Задача №171
Найти угол между касательными, проведенными из точки 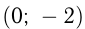 к параболе
к параболе 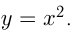
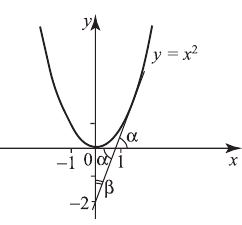
Решение:
Сделаем чертеж. 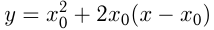 касательной к графику
касательной к графику 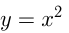 в точке с абсциссой
в точке с абсциссой 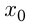 .
.
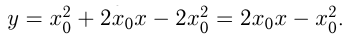
Эта прямая проходит через точку 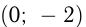 , поэтому
, поэтому 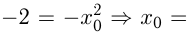
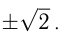 Возьмем касательную к правой ветви параболы;
Возьмем касательную к правой ветви параболы; 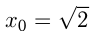 и
и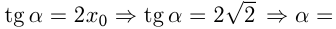
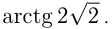
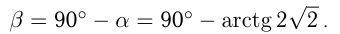
Угол между касательными 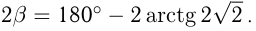
Ответ: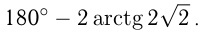
Задача №172
В точке 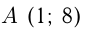 к графику функции
к графику функции 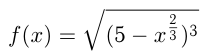 проведена касательная. Найти длину ее отрезка, заключенного между осями координат.
проведена касательная. Найти длину ее отрезка, заключенного между осями координат.
Решение:
Уравнение касательной к графику функции при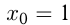 .
.
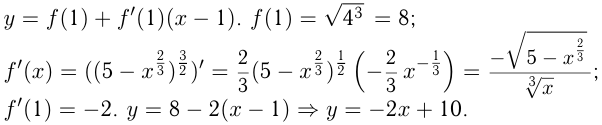
Прямая 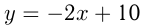 пересекает ось
пересекает ось 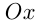 в точке
в точке 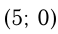 и ось
и ось 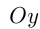 в точке
в точке 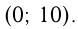 Расстояние между этими точками:
Расстояние между этими точками: 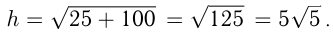
Ответ: 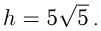
Задача №173
Найти уравнения тех касательных к графику функции 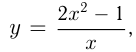 которые вместе с осями координат ограничивают треугольник площади
которые вместе с осями координат ограничивают треугольник площади 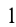 .
.
Решение:
Прямая 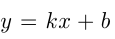 отсекает на осях
отсекает на осях 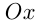 и
и 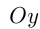 следующие отрезки:
следующие отрезки:
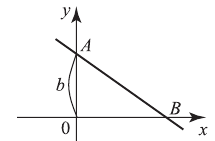
при 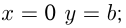
при 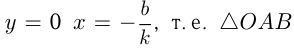 имеет катеты
имеет катеты 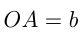 и
и 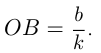
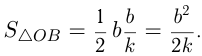
Уравнение касательной
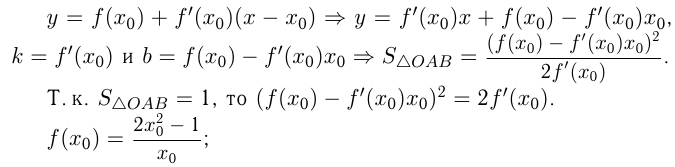
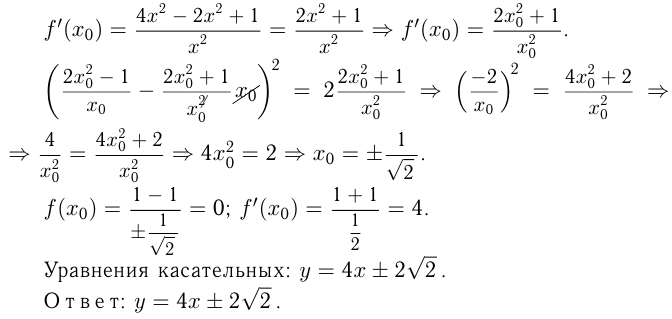
Исследование функций и построение графиков

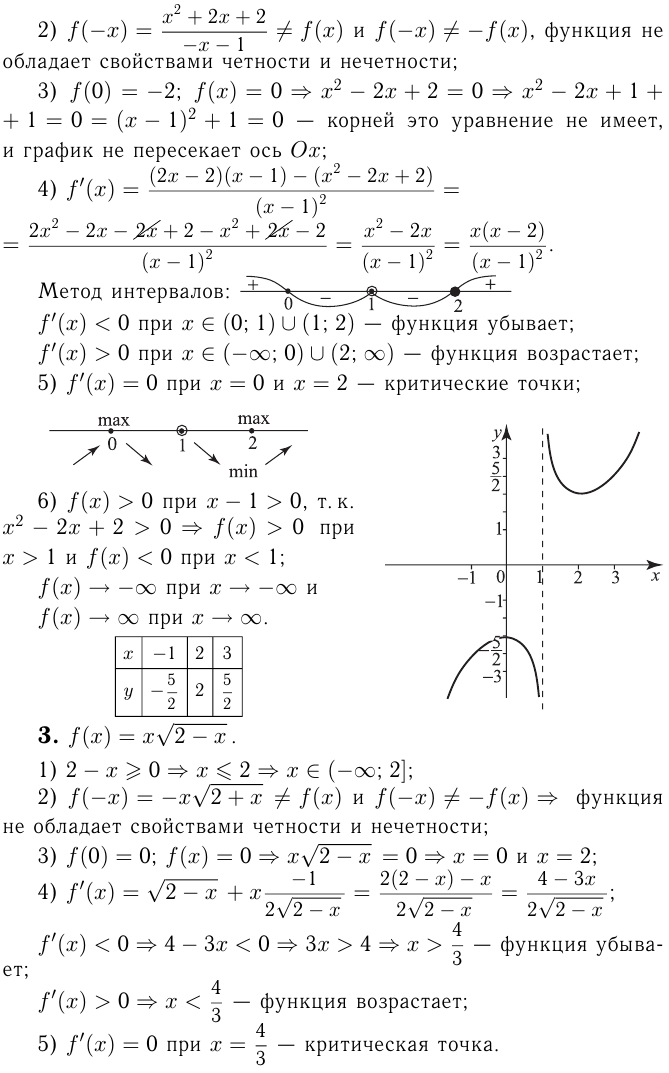



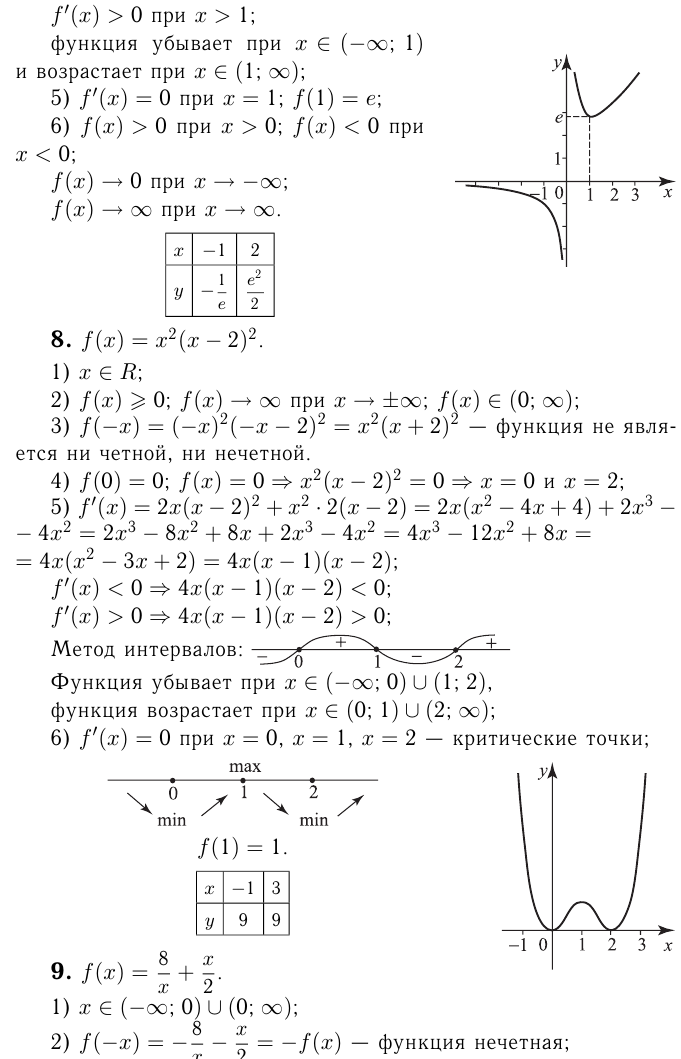
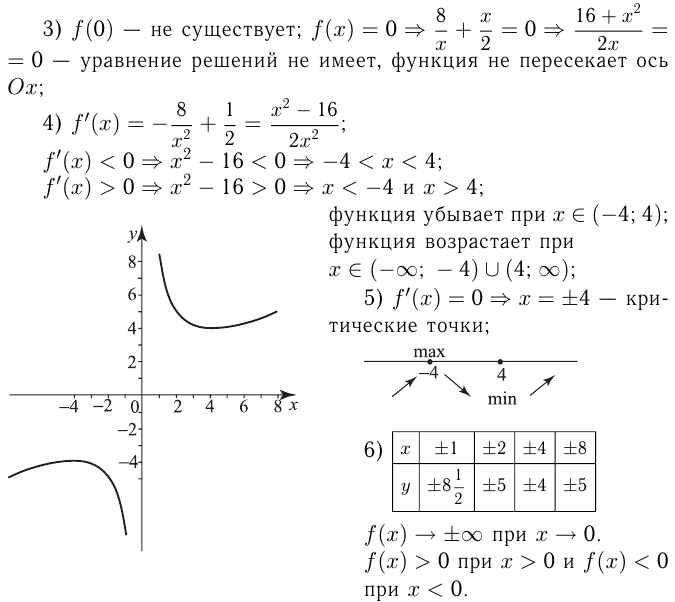
Наибольшее и наименьшее значение функции

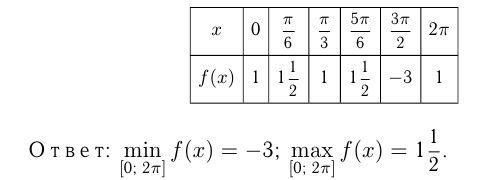



Первообразная и интеграл


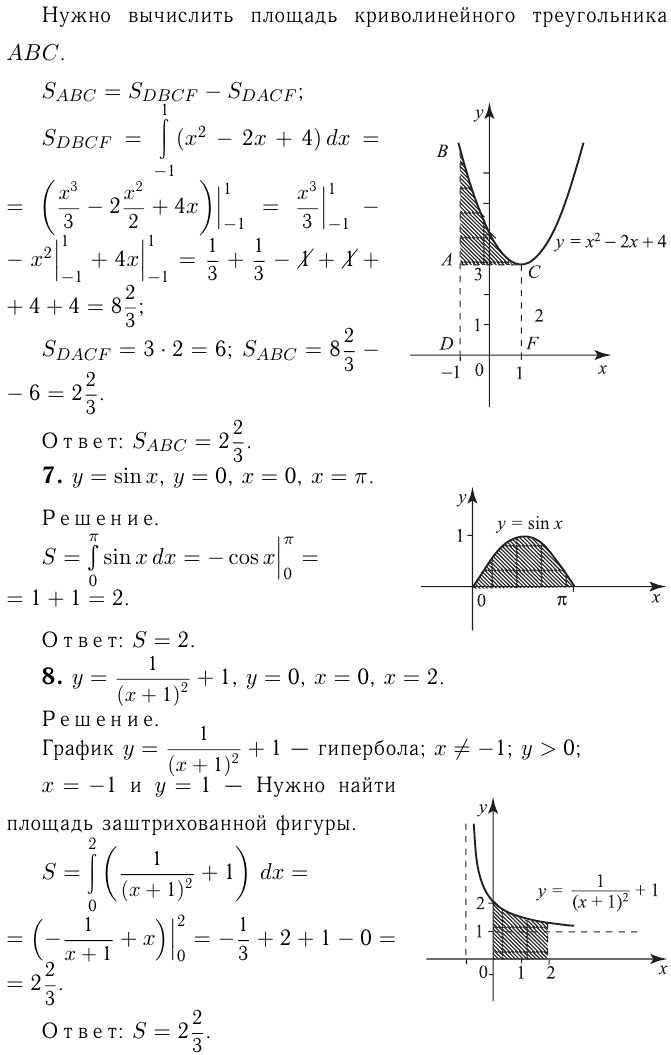

Эта лекция взята со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Решение задач с помощью неравенств |
| Решение задач на прогрессии по математике |
| Числа, числовые и алгебраические выражения |
| Законы сложения и умножения чисел в математике |

