Оглавление:
При решении задач на движение следует иметь в виду, что движение тел, о которых идет речь в задаче, если нет специальных оговорок, считается равномерным. Обычно вводятся следующие неизвестные: 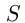 — путь,
— путь, 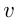 — скорость,
— скорость, 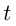 — время, в течение которого путь
— время, в течение которого путь 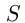 преодолевается со скоростью
преодолевается со скоростью 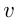 . Основная формула, использующаяся в этих задачах:
. Основная формула, использующаяся в этих задачах: 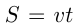 , и производные формулы:
, и производные формулы: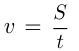 и
и 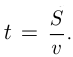 Возможны и другие обозначения, например, путь часто обозначают
Возможны и другие обозначения, например, путь часто обозначают 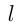 , скорость —
, скорость — 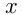 . Повороты движущихся тел считаются мгновенными, т.е. они происходят без затрат времени, скорости также меняются мгновенно. Если тело движется по течению реки, то его скорость складывается из его собственной скорости, т.е. скорости движения в стоячей воде, и скорости течения реки, а если оно движется против течения реки, то из его собственной скорости вычитается скорость течения реки. Можно записать так:
. Повороты движущихся тел считаются мгновенными, т.е. они происходят без затрат времени, скорости также меняются мгновенно. Если тело движется по течению реки, то его скорость складывается из его собственной скорости, т.е. скорости движения в стоячей воде, и скорости течения реки, а если оно движется против течения реки, то из его собственной скорости вычитается скорость течения реки. Можно записать так: 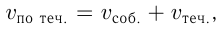
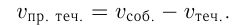 Считается, что плот движется со скоростью течения.
Считается, что плот движется со скоростью течения.
При решении задач на движение часто встречаются следующие две возможности:
1) движение навстречу друг другу; если два тела движутся навстречу друг другу со скоростями 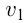 и
и 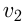 первоначальное расстояние между ними равно
первоначальное расстояние между ними равно 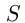 , то время, через которое они встретятся:
, то время, через которое они встретятся: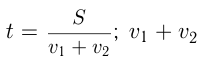 в этом случае — скорость сближения тел;
в этом случае — скорость сближения тел;
2) движение в одном направлении, когда скорость одного тела превышает скорость другого, и первое тело догоняет второе. Если первоначальное расстояние между ними равно 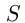 и
и 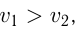 то время до их встречи
то время до их встречи 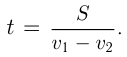 В этом случае скорость сближения
В этом случае скорость сближения 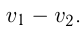
Задача №7
Поезд должен был пройти 220 км за определенное время. Через 2 часа после начала движения он был задержан на 10 мин и, чтобы прийти вовремя в пункт назначения, увеличил скорость на 5 км/ч. Найти первоначальную скорость поезда.
Решение:
Обозначим первоначальную скорость поезда 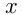 км/ч. Тогда на весь путь он должен был затратить
км/ч. Тогда на весь путь он должен был затратить 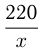 — часов. Реально он за 2 часа прошел
— часов. Реально он за 2 часа прошел 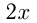 км, и ему осталось пройти
км, и ему осталось пройти 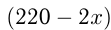 км. Последний участок пути он прошел со скоростью
км. Последний участок пути он прошел со скоростью 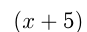 км/ч и затратил на него
км/ч и затратил на него 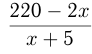 часов. 10 мин =
часов. 10 мин = 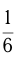 часа. Составим уравнение:
часа. Составим уравнение: 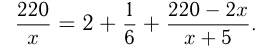
Решим уравнение:

Ответ: первоначальная скорость поезда 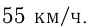
Задача №8
Моторная лодка, скорость которой в стоячей воде равна 15 км/ч, прошла 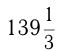 км вниз по течению реки и вернулась обратно. Найти скорость течения реки, если на весь путь затрачено 20 часов.
км вниз по течению реки и вернулась обратно. Найти скорость течения реки, если на весь путь затрачено 20 часов.
Решение:
Обозначим скорость течения реки 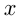 км/ч. Тогда скорость лодки по течению равна
км/ч. Тогда скорость лодки по течению равна 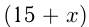 км/ч, ее скорость против течения равна
км/ч, ее скорость против течения равна 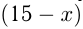 км/ч. Составим уравнение:
км/ч. Составим уравнение: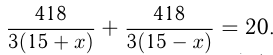
Решим уравнение: 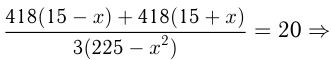
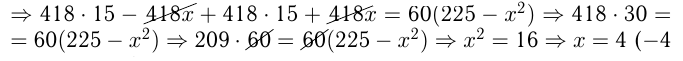
не подходит)
Ответ: скорость течения 4 км/ч.
Задача №9
Две автомашины выехали одновременно из одного пункта в одном и том же направлении. Одна машина движется со скоростью 50 км/ч, другая — 40 км/ч. Спустя полчаса из того же пункта в том же направлении выехала третья машина, которая обогнала 1-ю машину на 1 ч 30 мин позже, чем 2-ю. Найти скорость третьей машины.
Решение:
Пусть скорость 3-й машины 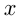 км/ч. Т.к. она обогнала две предыдущие машины, то
км/ч. Т.к. она обогнала две предыдущие машины, то 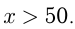 1-я машина за полчаса прошла
1-я машина за полчаса прошла 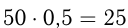 (км), 2-я машина
(км), 2-я машина 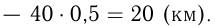 Соответствующие скорости сближения 1-й и 3-й машин, 2-й и 3-й машин:
Соответствующие скорости сближения 1-й и 3-й машин, 2-й и 3-й машин: 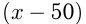 км/ч и
км/ч и 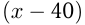 км/ч. Составим уравнение:
км/ч. Составим уравнение:
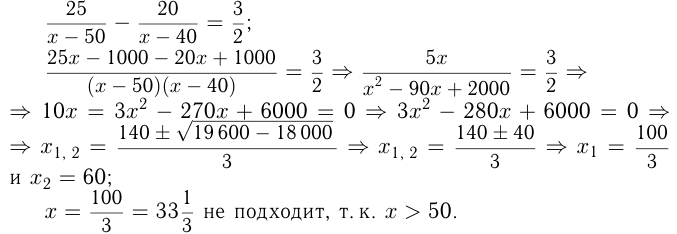
Ответ: скорость третьей машины 60 км/ч.
Задача №45
Стрекоза и муха двигаются по прямой. Стрекоза догоняет муху, их скорости равны 1,2 м/с и 0,3 м/с. Через сколько секунд расстояние между насекомыми сократится с 6,5 м до 20 см?
Решение:
Скорость сближения стрекозы и мухи равна разности их скоростей:
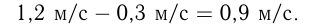
Расстояние, которое нужно преодолеть с этой скоростью, равно 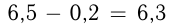 м. Следовательно, время равно
м. Следовательно, время равно 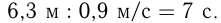
О т в е т: 7 с.
Задача №46
Из двух сел одновременно навстречу друг другу выехали автобус и грузовик. Через 0,5 ч они встретились. Какое расстояние между селами, если скорость автобуса 60, а грузовика 48 км/ч?
Решение:
Скорость сближения автобуса и грузовика: 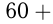
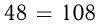 км/ч. Они ехали 0,5 ч, следовательно, расстояние между селами
км/ч. Они ехали 0,5 ч, следовательно, расстояние между селами 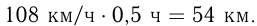
Задача №47
Катер прошел расстояние между пристанями по течению реки за 2 часа, а обратно против течения за 3 часа. Найти собственную скорость катера, если скорость течения реки 2 км/ч.
Решение:
Пусть собственная скорость катера 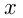 км/ч. Тогда его скорость по течению
км/ч. Тогда его скорость по течению 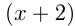 , а против течения
, а против течения 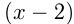 км/ч. Приравняем расстояния:
км/ч. Приравняем расстояния: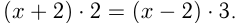
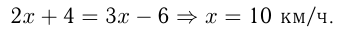
Ответ: собственная скорость катера 10 км/ч.
Задача №48
Пассажирский поезд проходит за 3 часа на 10 км больше, чем товарный за 4 часа. Скорость товарного поезда на 20 км/ч меньше скорости пассажирского. Найти скорость пассажирского поезда.
Решение. Пусть искомая скорость 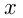 , тогда скорость товарного поезда
, тогда скорость товарного поезда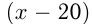 км/ч. За 3 часа пассажирский поезд проходит
км/ч. За 3 часа пассажирский поезд проходит 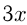 , а товарный за 4 часа
, а товарный за 4 часа  км. Уравнение
км. Уравнение 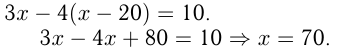
Ответ: скорость пассажирского поезда 70 км/ч.
Задача №49
Велосипедист и пешеход отправились из пунктов  и
и 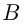 , расстояние между которыми 12 км, и встретились через 20 мин. Пешеход прибыл в пункт
, расстояние между которыми 12 км, и встретились через 20 мин. Пешеход прибыл в пункт  на 1 ч 36 мин позже, чем велосипедист в
на 1 ч 36 мин позже, чем велосипедист в 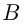 . Найти скорость пешехода.
. Найти скорость пешехода.
Решение. Пусть скорость пешехода 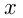 , а скорость велосипедиста
, а скорость велосипедиста 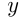 км/ч. Скорость их сближения
км/ч. Скорость их сближения 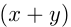 км/ч, поэтому
км/ч, поэтому
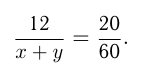
Время пешехода в пути 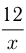 , время велосипедиста
, время велосипедиста 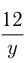 ч, поэтому
ч, поэтому
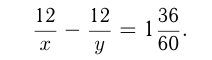
Решаем систему уравнений:
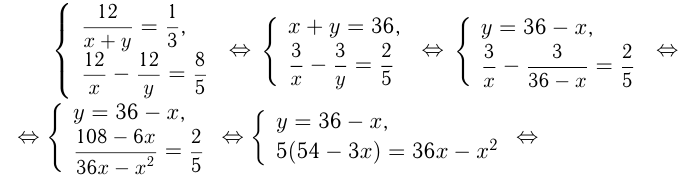
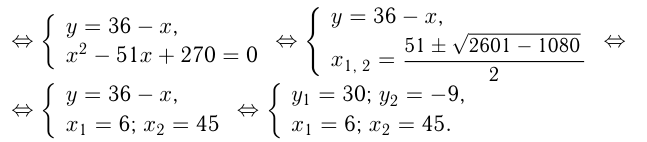
Пара чисел 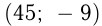 не подходит, т. к. скорость считается положительной.
не подходит, т. к. скорость считается положительной.
Ответ: скорость пешехода 6 км/ч.
Задача №50
Из пункта  в пункт
в пункт 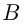 вышел товарный поезд. Спустя 3 ч вслед за ним вышел пассажирский поезд, скорость которого на 30 км/ч больше скорости товарного. Через 15 ч после своего выхода пассажирский поезд оказался впереди товарного на 300 км. Определить скорость товарного поезда.
вышел товарный поезд. Спустя 3 ч вслед за ним вышел пассажирский поезд, скорость которого на 30 км/ч больше скорости товарного. Через 15 ч после своего выхода пассажирский поезд оказался впереди товарного на 300 км. Определить скорость товарного поезда.
Решение. Пусть скорость товарного поезда 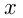 , тогда скорость пассажирского поезда
, тогда скорость пассажирского поезда 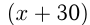 км/ч. Товарный поезд шел 18 ч и прошел расстояние
км/ч. Товарный поезд шел 18 ч и прошел расстояние 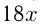 км, пассажирский поезд шел 15 ч и прошел расстояние
км, пассажирский поезд шел 15 ч и прошел расстояние 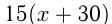 км. Получаем
км. Получаем
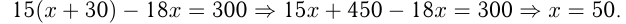
Ответ: скорость товарного поезда 50 км/ч.
Задача №51
Путь от  до
до 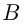 автомобиль проезжает с определенной скоростью за 2,5 часа. Если он увеличит скорость на 20 км/ч, то за 2 ч проедет на 15 км больше, чем расстояние от
автомобиль проезжает с определенной скоростью за 2,5 часа. Если он увеличит скорость на 20 км/ч, то за 2 ч проедет на 15 км больше, чем расстояние от  до
до 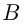 . Найти расстояние от
. Найти расстояние от  до
до  .
.
Решение. Пусть 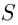 км — расстояние от
км — расстояние от  до
до  . Тогда неувеличенная скорость автомобиля
. Тогда неувеличенная скорость автомобиля 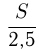 , а увеличенная
, а увеличенная 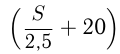 км/ч. Получаем
км/ч. Получаем 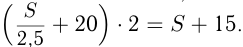 Решаем уравнение:
Решаем уравнение:

Ответ: расстояние 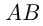 равно 125 км.
равно 125 км.
Задача №52
Половину пути мотоциклист ехал с намеченной скоростью 45 км/ч, затем задержался на 10 мин и поэтому, чтобы наверстать время, увеличил скорость на 15 км/ч. Каков весь путь мотоциклиста?
Решение. Примем весь путь за 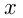 км. Тогда, если бы мотоциклист ехал с намеченной скоростью, он потратил бы времени
км. Тогда, если бы мотоциклист ехал с намеченной скоростью, он потратил бы времени 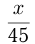 ч, но реально время его движения:
ч, но реально время его движения: 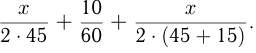 Поэтому
Поэтому
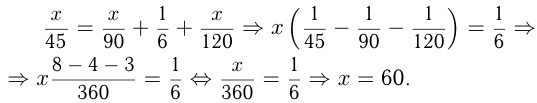
Ответ: путь мотоциклиста 60 км.
Задача №53
Расстояние между двумя пунктами поезд должен пройти за 10 часов. Пройдя первые 9 ч с намеченной скоростью, он снизил скорость на 7 км/ч и прибыл в конечный пункт с опозданием на 6 мин. Найти первоначальную скорость поезда.
Решение. Пусть первоначальная скорость поезда 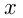 км/ч. Тогда расстояние между пунктами
км/ч. Тогда расстояние между пунктами 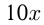
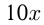
км. Поезд прошел снача-
ла 9х, затем (х — 7) км. Таким образом,
10х = 9® + (х — 7) • 1,1 =► х = 1,1.x — 7,7 => 0,1х = 7,7 => => х = 77.
Ответ: скорость поезда была 77 км/ч.
Задача №54
Велосипедист едет из одного города в другой со скоростью 10 км/ч. Если бы он ехал со скоростью 12 км/ч, то приехал бы в конечный пункт на 4 ч раньше. Какое расстояние преодолеет велосипедист?
Решение. Пусть расстояние между городами 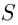 км. Тогда при скорости 10 км/ч велосипедист затратит на поездку
км. Тогда при скорости 10 км/ч велосипедист затратит на поездку 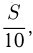 а при скорости 12 км/ч
а при скорости 12 км/ч 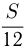 часов.
часов.
Уравнение 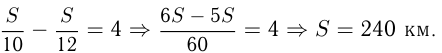
Ответ: 240 км.
Задача №55
Из города  в город
в город  выезжает велосипедист, а через 3 часа после его выезда из города
выезжает велосипедист, а через 3 часа после его выезда из города  навстречу ему выезжает мотоциклист, скорость которого в 3 раза больше скорости велосипедиста. Велосипедист и мотоциклист встречаются посередине между
навстречу ему выезжает мотоциклист, скорость которого в 3 раза больше скорости велосипедиста. Велосипедист и мотоциклист встречаются посередине между  и
и  . Если бы мотоциклист выехал не через 3, а через 2 часа после велосипедиста, то встреча произошла бы на 15 км ближе к
. Если бы мотоциклист выехал не через 3, а через 2 часа после велосипедиста, то встреча произошла бы на 15 км ближе к  . Найти расстояние между
. Найти расстояние между  и
и  .
.
Решение. Пусть расстояние 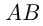 равно
равно 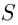 км, а скорость велосипедиста
км, а скорость велосипедиста 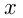 км/ч. Тогда скорость мотоциклиста
км/ч. Тогда скорость мотоциклиста 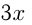 км/ч; время
км/ч; время 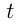 поездки в 1-м случае
поездки в 1-м случае
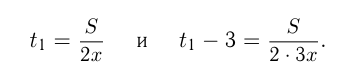

Ответ: расстояние 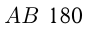 км.
км.
Задача №56
Города  и
и  расположены на берегу реки, причем город
расположены на берегу реки, причем город  расположен ниже по течению. Из этих городов одновременно навстречу друг другу выходят две лодки, которые встречаются посередине между городами
расположен ниже по течению. Из этих городов одновременно навстречу друг другу выходят две лодки, которые встречаются посередине между городами  и
и  . Продолжив свой путь после встречи в прежних направлениях и достигнув соответственно городов
. Продолжив свой путь после встречи в прежних направлениях и достигнув соответственно городов  и
и  , лодки мгновенно поворачивают обратно и встречаются вновь на 20 км ближе к городу
, лодки мгновенно поворачивают обратно и встречаются вновь на 20 км ближе к городу  . Если бы те же лодки, выйдя одновременно из
. Если бы те же лодки, выйдя одновременно из  и
и  , поплыли обе против течения, то лодка из
, поплыли обе против течения, то лодка из  догнала бы лодку из
догнала бы лодку из  в 150 км от
в 150 км от . Найти расстояние от
. Найти расстояние от  до
до  .
.
Решение.
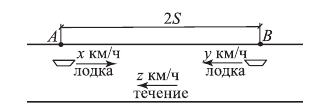
Обозначим: 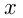 км/ч — собственная скорость лодки, вышедшей из
км/ч — собственная скорость лодки, вышедшей из  ;
; 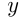 км/ч — собственная скорость лодки, вышедшей из
км/ч — собственная скорость лодки, вышедшей из  ;
; 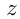 км/ч — скорость течения;
км/ч — скорость течения; 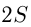 км — расстояние между
км — расстояние между  и
и  . Тогда 1-е условие дает соотношение:
. Тогда 1-е условие дает соотношение:
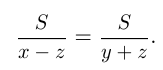
Из 2-го условия следует:
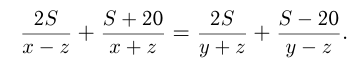
И из 3-го условия следует:
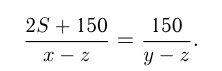
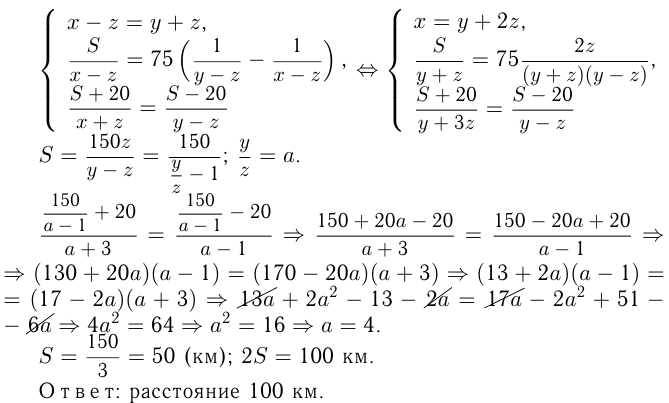
Задача №57
Автомобиль с грузом ехал из одного города в другой со скоростью 60 км/ч, а возвращался обратно порожняком со скоростью 100 км/ч. Найти среднюю скорость автомобиля.
Решение. Пусть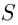 км — расстояние между городами, тогда
км — расстояние между городами, тогда 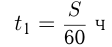 — время движения автомобиля с грузом и
— время движения автомобиля с грузом и 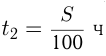 время движения автомобиля обратно.
время движения автомобиля обратно.
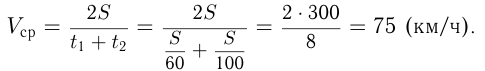
Ответ: средняя скорость автомобиля 75 км/ч.
Задача №58
Поезд прошел мимо наблюдателя за 6 сек, а по мосту длиной 350 метров проходил в течение 20 сек. Найти скорость и длину поезда.
Решение. Пусть 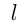 м — длина поезда и
м — длина поезда и 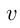 м/сек — его скорость.
м/сек — его скорость.
Тогда имеем систему:
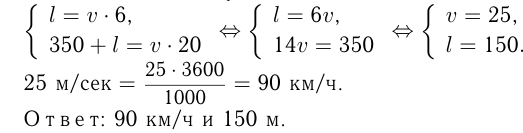
Задача №59
В гору ехал автомобиль. В 1-ю секунду после достижения пункта  он проехал 30 м, а в каждую следующую секунду он проезжал на 2 м меньше, чем в предыдущую. Через 9 сек после того, как автомобиль достиг пункта
он проехал 30 м, а в каждую следующую секунду он проезжал на 2 м меньше, чем в предыдущую. Через 9 сек после того, как автомобиль достиг пункта  , навстречу ему выехал автобус из пункта
, навстречу ему выехал автобус из пункта  , находящегося на расстоянии 258 м от пункта
, находящегося на расстоянии 258 м от пункта  . В 1-ю секунду автобус проехал 2 м, а в каждую следующую секунду он проезжал на 1 м больше, чем в предыдущую. Какое расстояние проехал автобус до встречи с автомобилем?
. В 1-ю секунду автобус проехал 2 м, а в каждую следующую секунду он проезжал на 1 м больше, чем в предыдущую. Какое расстояние проехал автобус до встречи с автомобилем?
Решение.

Автомобиль за 9 сек проехал расстояние  , причем
, причем  может быть найдено как сумма
может быть найдено как сумма 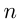 членов арифметической прогрессии:
членов арифметической прогрессии:
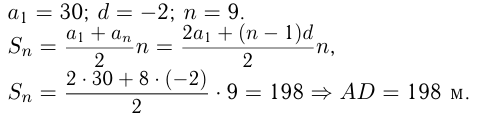
Расстояние 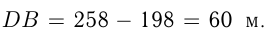 Пусть автомобиль из
Пусть автомобиль из 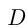 и автобус из
и автобус из  двигались навстречу друг другу до встречи
двигались навстречу друг другу до встречи 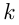 сек. Тогда путь автомобиля считается как сумма к членов арифметической прогрессии:
сек. Тогда путь автомобиля считается как сумма к членов арифметической прогрессии: 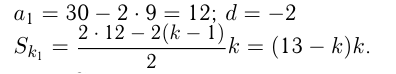
Путь автобуса также можно посчитать как сумму 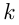 членов арифметической прогрессии:
членов арифметической прогрессии: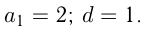
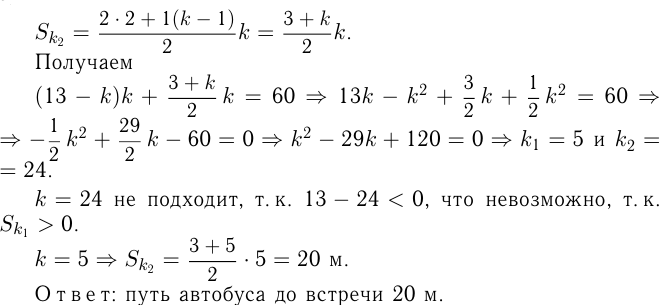
Задача №60
Из пункта  в пункт
в пункт  выехал грузовой автомобиль. Через 1 ч из пункта
выехал грузовой автомобиль. Через 1 ч из пункта  в пункт
в пункт  выехал легковой автомобиль, который прибыл в пункт
выехал легковой автомобиль, который прибыл в пункт  одновременно с грузовым автомобилем. Если бы грузовой и легковой автомобили одновременно выехали из пунктов
одновременно с грузовым автомобилем. Если бы грузовой и легковой автомобили одновременно выехали из пунктов  и
и  навстречу друг другу, то они бы встретились через 1 ч 12 мин после выезда. Сколько времени провел в пути от
навстречу друг другу, то они бы встретились через 1 ч 12 мин после выезда. Сколько времени провел в пути от  до
до  грузовой автомобиль?
грузовой автомобиль?
Решение. Пусть легковой автомобиль был в пути 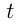 , а грузовой —
, а грузовой —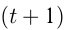 ч; путь от
ч; путь от  до
до  —
— 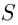 км. Тогда скорость легкового автомобиля
км. Тогда скорость легкового автомобиля 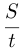 , а грузового —
, а грузового — 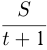 км/ч. Из условия
км/ч. Из условия
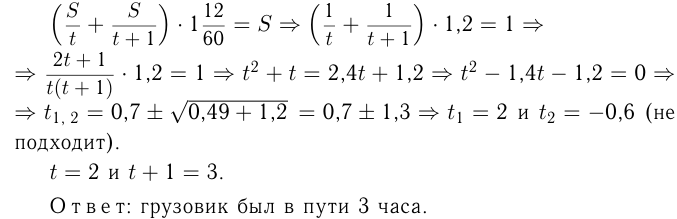
Задача №61
На полпути между городами 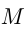 и
и 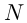 , расстояние между которыми 280 км, расположен поселок
, расстояние между которыми 280 км, расположен поселок 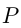 . Из
. Из 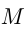 и
и 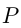 одновременно выехали навстречу друг другу автобус и грузовик: автобус — из
одновременно выехали навстречу друг другу автобус и грузовик: автобус — из 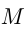 , грузовик — из
, грузовик — из 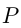 . Автобус прибыл в
. Автобус прибыл в 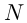 одновременно с прибытием грузовика в
одновременно с прибытием грузовика в 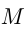 . Затем обе машины одновременно выехали навстречу друг другу, встретились в пункте
. Затем обе машины одновременно выехали навстречу друг другу, встретились в пункте  и прибыли одновременно: автобус в
и прибыли одновременно: автобус в 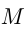 , а грузовик в
, а грузовик в 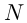 . Найти расстояние от города
. Найти расстояние от города 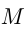 до пункта
до пункта  , если известно, что автобус и грузовик двигались каждый со своей постоянной скоростью и оба сделали остановки одинаковой продолжительности: автобус — на пути от
, если известно, что автобус и грузовик двигались каждый со своей постоянной скоростью и оба сделали остановки одинаковой продолжительности: автобус — на пути от 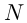 к
к  , а грузовик — на пути от
, а грузовик — на пути от 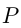 к
к 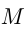 .
.
Решение.
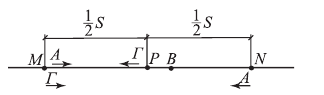
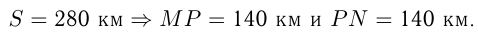
Пусть 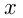 км/ч — скорость автобуса;
км/ч — скорость автобуса; 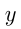 км/ч — скорость грузовика;
км/ч — скорость грузовика; 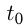 ч — продолжительность остановок;
ч — продолжительность остановок; 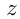 км — расстояние
км — расстояние 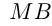 . Тогда из условий имеем систему:
. Тогда из условий имеем систему:

Задача №62
Из пункта  в пункт
в пункт  по течению отплывает лодка. Одновременно с ней из
по течению отплывает лодка. Одновременно с ней из  против течения отправляется катер, который, прибыв в
против течения отправляется катер, который, прибыв в  , не останавливаясь, следует обратно в
, не останавливаясь, следует обратно в  , а из
, а из  также без остановки отправляется в
также без остановки отправляется в  . На этом последнем участке маршрута катер опять встречает лодку, которая прошла к этому моменту
. На этом последнем участке маршрута катер опять встречает лодку, которая прошла к этому моменту 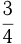 пути от
пути от  до
до  . Скорость лодки при движении по течению в 9 раз больше ее скорости против течения. Во сколько раз скорость катера по течению больше скорости лодки по течению? Решение.
. Скорость лодки при движении по течению в 9 раз больше ее скорости против течения. Во сколько раз скорость катера по течению больше скорости лодки по течению? Решение.

Пусть 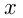 км/ч — собственная скорость лодки;
км/ч — собственная скорость лодки; 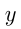 км/ч — собственная скорость катера;
км/ч — собственная скорость катера; 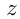 км/ч — скорость течения;
км/ч — скорость течения; 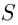 — путь
— путь 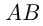 . Тогда
. Тогда 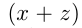 и
и  км/ч — скорость лодки по и против течения;
км/ч — скорость лодки по и против течения; 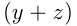 и
и  км/ч — скорость катера по и против течения. Тогда из условий
км/ч — скорость катера по и против течения. Тогда из условий
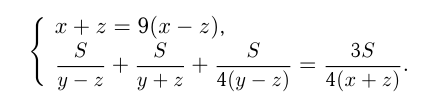
Требуется определить 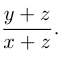
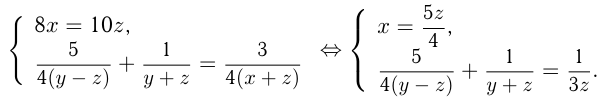
Решаем 2-е уравнение:
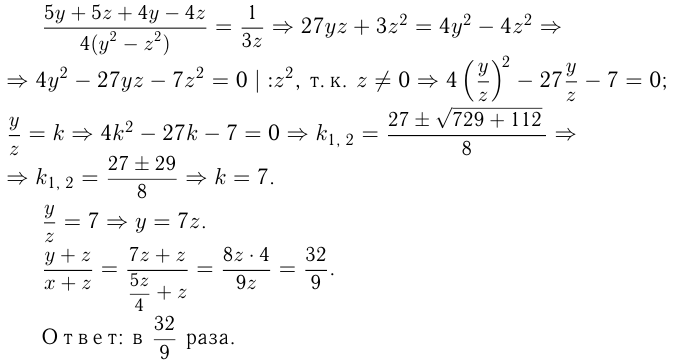
Задача №63
Из двух пунктов одновременно навстречу друг другу вышли два пешехода. Определить, через сколько времени они встретятся, зная следующее: если бы один из пешеходов шел вдвое быстрее, то встреча произошла бы на полчаса раньше, а если бы вдвое быстрее шел другой — то на 48 мин раньше.
Решение.

Введенные обозначения и условия задачи позволяют написать систему трех уравнений с 4-мя неизвестными, где 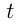 час — время до встречи при движении пешеходов с первоначальными скоростями.
час — время до встречи при движении пешеходов с первоначальными скоростями.
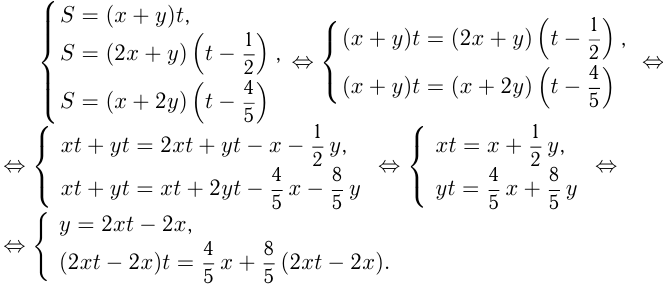
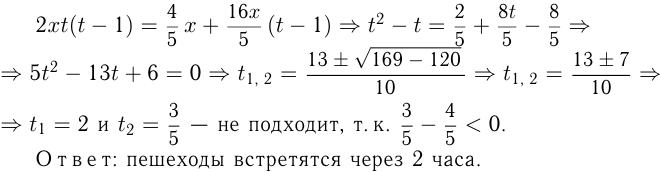
Задача №64
Из пунктов  и
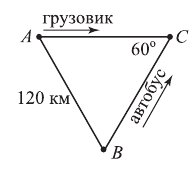
и  , находящихся друг от друга на расстоянии 120 км, по прямолинейным дорогам, сходящимся в пункте
, находящихся друг от друга на расстоянии 120 км, по прямолинейным дорогам, сходящимся в пункте 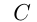 под углом 60°, одновременно выехали грузовик и автобус соответственно со скоростями 40 и 60 км/ч. Автобус прибыл в пункт
под углом 60°, одновременно выехали грузовик и автобус соответственно со скоростями 40 и 60 км/ч. Автобус прибыл в пункт 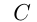 на 1 ч раньше грузовика. Найти время движения автобуса.
на 1 ч раньше грузовика. Найти время движения автобуса.
Решение. Пусть 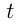 ч — время движения автобуса.
ч — время движения автобуса.
Расстояние 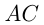 равно
равно 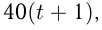 расстояние
расстояние  км.
км.
По теореме косинусов
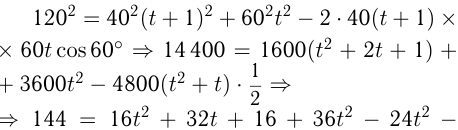
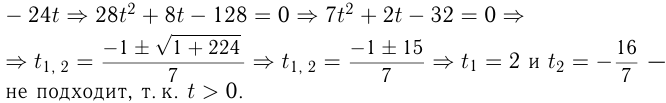
Ответ: автобус ехал 2 часа.
Задача №65
Пункты  ,
,  ,
, 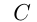 удалены от пункта
удалены от пункта 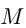 соответственно на 60, 55 и 56 км. Одновременно из этих пунктов в пункт
соответственно на 60, 55 и 56 км. Одновременно из этих пунктов в пункт 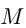 вышли 3 пешехода: 1-й из
вышли 3 пешехода: 1-й из  , 2-й из
, 2-й из  и 3-й из
и 3-й из 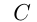 . 1-й прошел весь путь с постоянной скоростью и прибыл в
. 1-й прошел весь путь с постоянной скоростью и прибыл в 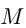 на 2 ч раньше 2-го и 3-го, прибывших одновременно. 2-й пешеход, пройдя 40 км с той же скоростью, что и 1-й, сделал остановку на 1 ч. Остаток пути он прошел со скоростью, которая меньше скорости 3-го пешехода на столько же, на сколько скорость 3-го меньше скорости 1-го пешехода. 3-й пешеход прошел весь путь с постоянной скоростью. Определить скорости 1-го и 3-го пешеходов.
на 2 ч раньше 2-го и 3-го, прибывших одновременно. 2-й пешеход, пройдя 40 км с той же скоростью, что и 1-й, сделал остановку на 1 ч. Остаток пути он прошел со скоростью, которая меньше скорости 3-го пешехода на столько же, на сколько скорость 3-го меньше скорости 1-го пешехода. 3-й пешеход прошел весь путь с постоянной скоростью. Определить скорости 1-го и 3-го пешеходов.
Решение.

Задача №66
Из 2-х пунктов, расстояние между которыми 2400 км, навстречу друг другу выезжают одновременно пассажирский и скорый поезда. Каждый из них едет с постоянной скоростью, и в некоторый момент они встречаются. Если бы оба поезда шли со скоростью скорого, то их встреча произошла бы на 3 часа раньше, если бы оба поезда шли со скоростью пассажирского, то их встреча произошла бы на 5 часов позже фактического момента встречи. Найти скорости поездов.
Решение. Пусть 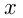 км/ч — скорость пассажирского и
км/ч — скорость пассажирского и 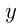 км/ч — скорого поезда. Тогда
км/ч — скорого поезда. Тогда 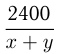 — время движения поездов до встречи. Из условий получаем:
— время движения поездов до встречи. Из условий получаем:

Задача №67
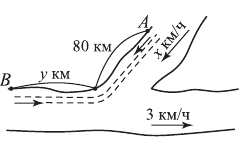
В реку впадает приток. Пароход отходит от пристани  на притоке, идет вниз по течению 80 км до реки, далее по реке вверх против течения до пристани
на притоке, идет вниз по течению 80 км до реки, далее по реке вверх против течения до пристани  , затратив 18 часов на весь путь от
, затратив 18 часов на весь путь от  до
до  . Затем пароход возвращается обратно. Время обратного движения от
. Затем пароход возвращается обратно. Время обратного движения от  до
до  по тому же пути равно 15 часам. Собственная скорость парохода равна 18 км/ч. Скорость течения реки равна 3 км/ч. Каково расстояние от пристани
по тому же пути равно 15 часам. Собственная скорость парохода равна 18 км/ч. Скорость течения реки равна 3 км/ч. Каково расстояние от пристани  до пристани
до пристани  и какова скорость притока?
и какова скорость притока?
Решение.
Пусть 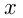 км/ч — скорость притока;
км/ч — скорость притока; 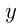 км — расстояние от пристани
км — расстояние от пристани  до впадения притока в реку. Тогда из условий имеем систему двух уравнений:
до впадения притока в реку. Тогда из условий имеем систему двух уравнений:

Задача №68
Две реки с прямолинейными руслами и одинаковой скоростью течения впадают в одном и том же месте в озеро, образуя между собой угол 60°. От двух причалов, расположенных на разных реках и отстоящих друг от друга на расстоянии 28 км, одновременно вышли байдарка и лодка, скорости которых в стоячей воде соответственно равны 10 и 3 км/ч. Байдарка достигла озера через 2, а лодка — через 4 часа. Найти скорость течения реки.
Решение.
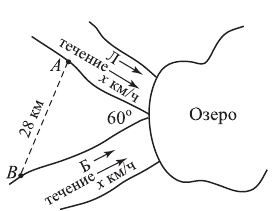
Путь лодки от  до озера
до озера 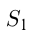 :
: 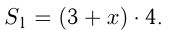 Путь байдарки от
Путь байдарки от  до озера
до озера 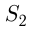 :
: 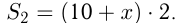
По теореме косинусов
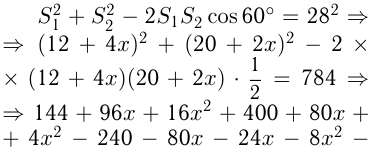
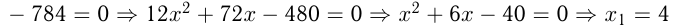
и 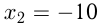 (не подходит, т. к.
(не подходит, т. к. 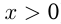 ).
).
Ответ: скорость течения реки 4 км/ч.
Задача №69
Две точки движутся по окружности длиной 120 м с постоянными скоростями. Если они движутся в разных направлениях, то встречаются через каждые 15 сек. При движении в одном направлении одна точка догоняет другую через каждые 60 сек. Найти скорости точек.
Решение.
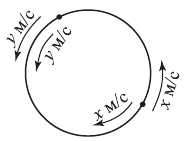
Пусть одна точка движется со скоростью 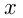 , а другая —
, а другая — 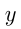 м/с;
м/с; 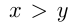 . Тогда, если они движутся навстречу друг другу, tsj- то за 15 сек вместе описывают окружность:
. Тогда, если они движутся навстречу друг другу, tsj- то за 15 сек вместе описывают окружность: 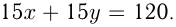 Если они движутся, догоняя одна другую, то
Если они движутся, догоняя одна другую, то 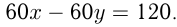
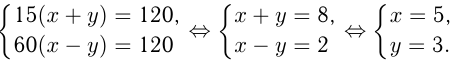
Ответ: скорости точек 5 и 3 м/с.
Задача №70
Из пункта  в пункт
в пункт  отправился скорый поезд. Одновременно навстречу ему из
отправился скорый поезд. Одновременно навстречу ему из  в
в  вышел товарный поезд, который встретился со скорым через
вышел товарный поезд, который встретился со скорым через 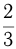 часа после отправления. Расстояние между
часа после отправления. Расстояние между  и
и  равно 80 км, поезда двигались с постоянными скоростями. С какой скоростью двигался скорый поезд, если 40 км он шел на
равно 80 км, поезда двигались с постоянными скоростями. С какой скоростью двигался скорый поезд, если 40 км он шел на 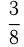 часа дольше, чем товарный поезд шел 5 км?
часа дольше, чем товарный поезд шел 5 км?
Решение.

Обозначим через 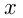 и
и 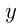 скорости скорого и товарного поездов. Из условия, до встречи поездов в
скорости скорого и товарного поездов. Из условия, до встречи поездов в 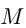 прошло
прошло 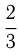 часа, значит можно написать уравнение:
часа, значит можно написать уравнение: 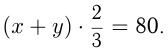 Из 2-го условия
Из 2-го условия 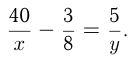
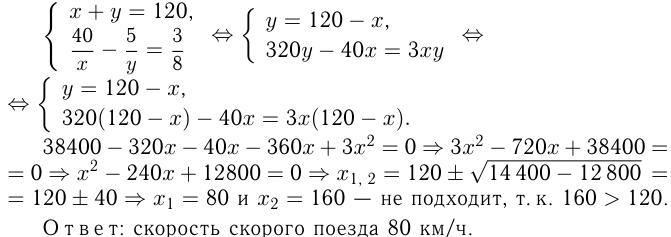
Задача №71
Пароход, отчалив от пристани  , спустился вниз по течению реки на 60 км до устья впадающего в реку притока и поднялся вверх по притоку на 20 км до пристани
, спустился вниз по течению реки на 60 км до устья впадающего в реку притока и поднялся вверх по притоку на 20 км до пристани  . Весь путь от
. Весь путь от  до
до  пароход прошел за 7 часов. Скорость течения реки и скорость течения притока равны 1 км/ч. Найти собственную скорость парохода.
пароход прошел за 7 часов. Скорость течения реки и скорость течения притока равны 1 км/ч. Найти собственную скорость парохода.
Решение.
Пусть собственная скорость парохода 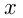 км/ч. Тогда при движении по течению реки он затратил
км/ч. Тогда при движении по течению реки он затратил 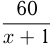 часов, а при движении против течения притока —
часов, а при движении против течения притока — 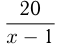 часов. По условию
часов. По условию
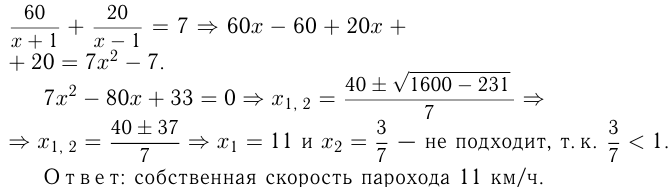
Задача №72
Два тела движутся по окружности равномерно в одну сторону, причем 1-е тело проходит окружность на 2 сек быстрее 2-го и догоняет 2-е тело каждые 12 сек. За какое время каждое тело проходит окружность?
Решение. Пусть 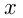 и
и 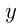 м/с
м/с 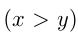 — скорости движения тел по окружности,
— скорости движения тел по окружности, 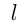 — длина окружности. Тогда из условий задачи
— длина окружности. Тогда из условий задачи
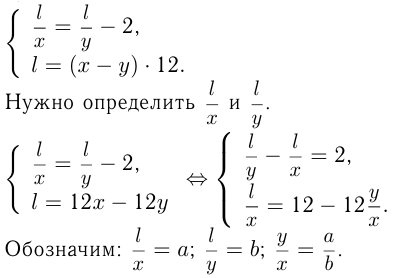
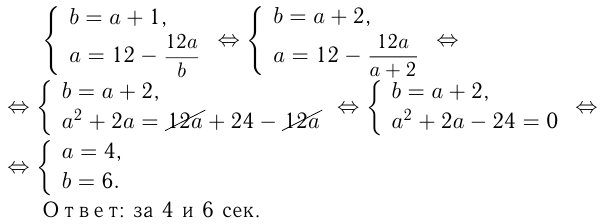
Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Решение задач на проценты по математике |
| Решение задач на смеси, процентное содержание и концентрации по математике |
| Решение задач на работу по математике |
| Решение задач на части по математике |

