Оглавление:
Для успешного решения задач на числа нужно знать о системах счисления, в частности о десятеричной системе счисления. Всем хорошо известно, что те числа, которыми мы постоянно пользуемся, состоят из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, и величина числа зависит от места (позиции) цифры в числе. Это означает, что мы используем десятеричную позиционную систему счисления. Каждое число в этой системе счисления представляется как 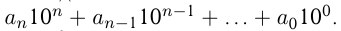 Так,
Так, 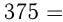
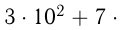
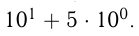 В
В 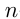 -значном числе старшая степень 10 равна
-значном числе старшая степень 10 равна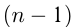 . Это видно в предыдущем примере. Еще пример:
. Это видно в предыдущем примере. Еще пример:
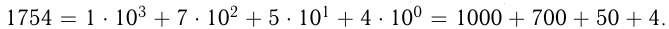
При записи числа, когда цифры обозначены буквами, используется черта сверху, например, 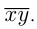
Задача №17
Сумма квадратов цифр положительного двузначного числа равна 13. Если из этого числа вычесть 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найти число.
Решение:
Пусть цифры двузначного числа 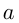 и
и 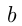 , а само число
, а само число 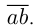 Это значит, что число можно записать как
Это значит, что число можно записать как 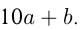 Из условий:
Из условий:
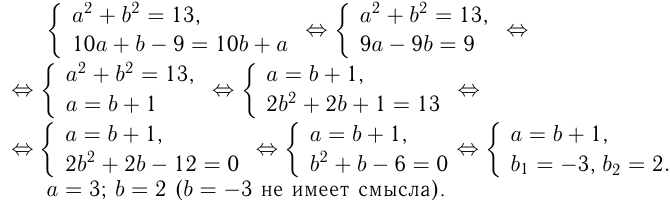
Ответ: число 32.
Задача №18
Задумано целое положительное число. К его записи присоединили справа цифру 5 и из полученного нового числа вычли квадрат задуманного числа. Разность разделили на задуманное число, а затем вычли задуманное число и в результате получили единицу. Какое число было задумано?
Решение:
Допустим, задумали число 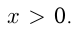 При присоединении справа 5-ти, число увеличилось в 10 раз из-за сдвига позиций и на 5 единиц, т.е. стало
При присоединении справа 5-ти, число увеличилось в 10 раз из-за сдвига позиций и на 5 единиц, т.е. стало 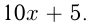 Из условий:
Из условий: 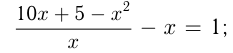
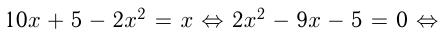
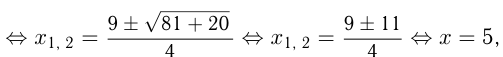
т. к. 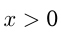 и целое.
и целое.
Ответ: задумано число 5.
Задача №19
Если двузначное число разделить на сумму его цифр, то в частном получится 3 и в остатке 7. Если взять сумму квадратов цифр этого числа и вычесть из нее произведение тех же цифр, то получится первоначальное число. Найти это число.
Решение:
Пусть имеется двузначное число 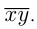 . Из условий получаем:
. Из условий получаем:
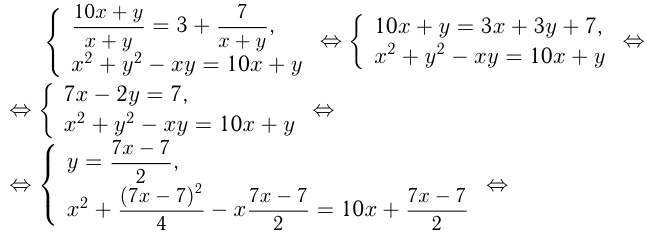
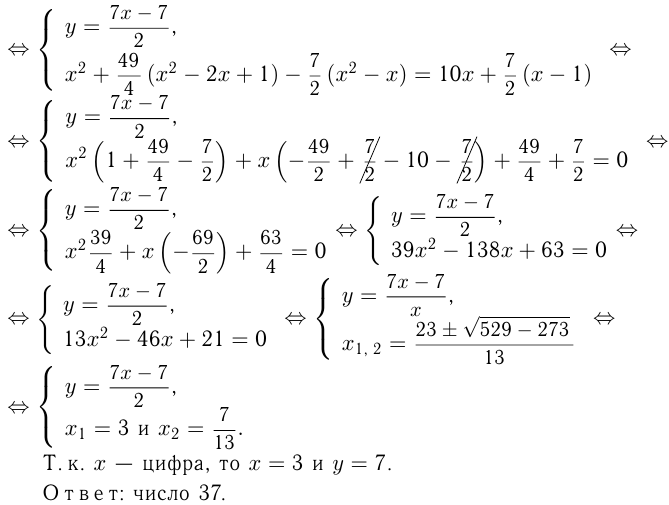
Задача №95
Найти число, если известно, что после вычитания из него 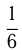 его части и прибавления к полученной разности его пятой части получится 9,3.
его части и прибавления к полученной разности его пятой части получится 9,3.
Решение:
Обозначим искомое число 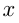 . По условию:
. По условию: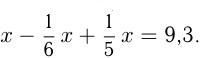
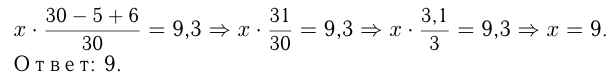
Задача №96
При разделке туши барана треть веса составляет туловище, одну пятую — голова, шестую часть — ноги, четверть — шкура и еще 6 кг — внутренности. Сколько весит целый баран?
Решение:
Если вес целого барана 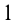 , то
, то 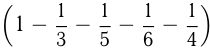 — часть, которую составляют внутренности.
— часть, которую составляют внутренности.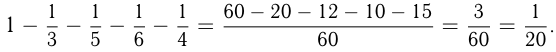
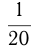 — туши — это 6 кг, следовательно, вся туша — это
— туши — это 6 кг, следовательно, вся туша — это 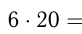
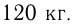
Ответ: целый баран весит 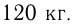 .
.
Задача №97
Автомобиль выехал, имея на борту груз, составляющий 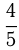 его грузоподъемности. На 1-й остановке он выгрузил
его грузоподъемности. На 1-й остановке он выгрузил 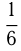 часть груза, на 2-й взял на борт
часть груза, на 2-й взял на борт 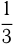 своей грузоподъемности, на 3-й выгрузил —
своей грузоподъемности, на 3-й выгрузил — 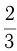 привезенного груза. В результате в пункт прибытия он привез 5 т. Какова грузоподъемность автомобиля?
привезенного груза. В результате в пункт прибытия он привез 5 т. Какова грузоподъемность автомобиля?
Решение:
Пусть грузоподъемность автомобиля 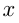 т, тогда его первоначальный груз
т, тогда его первоначальный груз 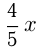 т, после 1-й остановки его груз
т, после 1-й остановки его груз
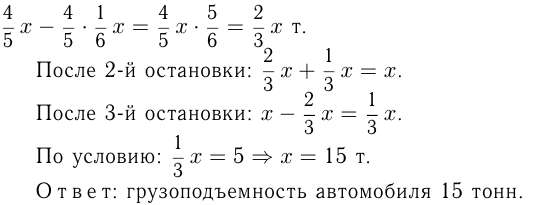
Задача №98
Рыбу разрезали на 5 кусков в отношении по весу 14:12:11:9:15, причем 2-й кусок весил 112 г. Сколько весила вся рыба?
Решение:
2-й кусок составляет 12 частей от всей рыбы, а вся рыба 14+12+11-1-94-15 = 61 часть. 112 г соответствует 12-ти частям 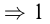 часть —
часть — 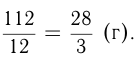 Вся рыба
Вся рыба 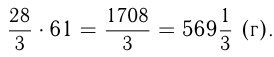
Ответ: вся рыба весила 569- г.
Задача №99
В двух колоннах по 28 автомобилей в каждой, было 11 «Жигулей», остальные — «Москвичи». Сколько «Москвичей» было в каждой колонне, если известно, что в 1-й из них на каждую машину «Жигули» приходилось в 2 раза больше «Москвичей», чем во 2-й?
Решение:
Пусть в 1-й колонне 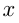 «Жигулей», тогда во 2-й
«Жигулей», тогда во 2-й 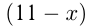 «Жигулей».
«Жигулей».
Запишем отношение:

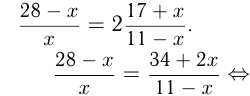
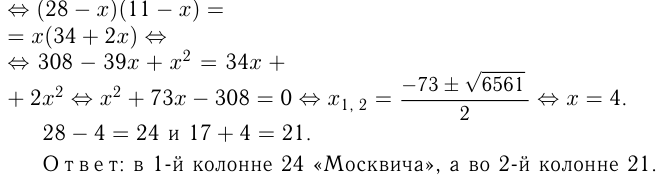
Задача №100
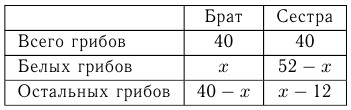
Брат и сестра собрали каждый по 40 грибов, из них 52 белых. Сколько белых грибов собрал каждый, если известно, что отношение числа белых грибов к числу остальных грибов у брата в 4 раза больше, чем у сестры?
Решение:
Допустим, брат собрал 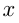 белых грибов.
белых грибов.
Составим отношение:
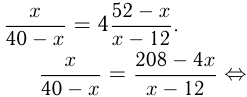

Задача №101
Сумма цифр двузначного числа равна 12. Если к искомому числу прибавить 36, то получится число, записанное теми же цифрами, но в обратном порядке. Найти число.
Решение:
Пусть двузначное число записано как 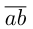 , т.е. а — число
, т.е. а — число 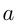 десятков,
десятков, 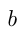 — число единиц. Иначе это число можно записать как
— число единиц. Иначе это число можно записать как 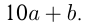 Число с теми же цифрами, но записанными в обратом порядке:
Число с теми же цифрами, но записанными в обратом порядке: 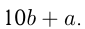 Из условий:
Из условий:
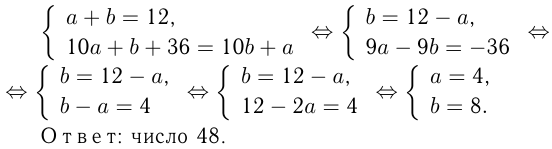
Задача №102
Числители трех данных дробей пропорциональны числам 1, 2 и 3, а обратные величины соответствующих знаменателей пропорциональны числам 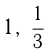 и
и 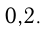 Найти эти дроби, если их среднее арифметическое равно
Найти эти дроби, если их среднее арифметическое равно 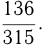
Решение:
Даны дроби: 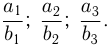
Известно: 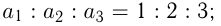

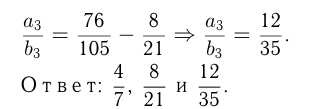
Задача №103
Вкладчик взял из банка сначала 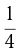 своих денег, потом
своих денег, потом 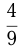 оставшихся и еще 64 рубля. После этого у него осталось в банке
оставшихся и еще 64 рубля. После этого у него осталось в банке 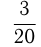 — всех его денег. Как велик был вклад?
— всех его денег. Как велик был вклад?
Решение:
Пусть вклад был 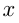 руб. Тогда сначала взято
руб. Тогда сначала взято 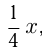 осталось
осталось 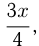 потом взято
потом взято 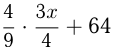 . По условию:
. По условию:
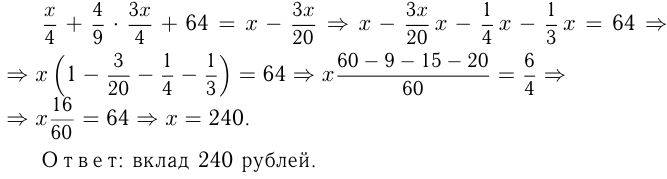
Задача №104
Сумма квадратов цифр двузначного числа равна 13. Если от этого двузначного числа отнять 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найти число.
Решение:
Дано число 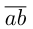 , где
, где 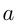 — число десятков,
— число десятков, 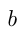 — число единиц. По условию:
— число единиц. По условию:
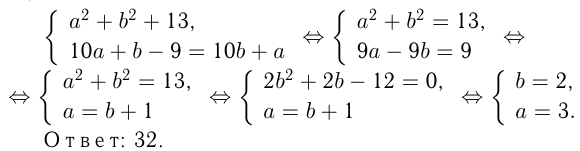
Задача №105
Площади трех участков земли находятся в отношении 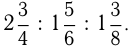 Известно, что с 1-го участка собрано зерна на 72 ц больше, чем со 2-го. Найти общую площадь всех трех участков, если средняя урожайность составляет 18 ц/га.
Известно, что с 1-го участка собрано зерна на 72 ц больше, чем со 2-го. Найти общую площадь всех трех участков, если средняя урожайность составляет 18 ц/га.
Решение:
Если 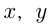 и
и 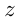 га — площади участков, то:
га — площади участков, то:
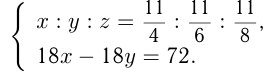
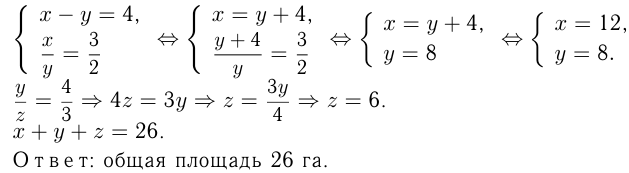
Задача №106
Первое из неизвестных чисел составляет 140% второго, а отношение первого к третьему равно 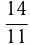 . Найти эти числа, если разность между 3-м и 2-м на 40 меньше числа, составляющего 12,5% суммы 1-го и 2-го чисел.
. Найти эти числа, если разность между 3-м и 2-м на 40 меньше числа, составляющего 12,5% суммы 1-го и 2-го чисел.
Решение:
Обозначим неизвестные числа 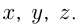 Запишем условия:
Запишем условия:
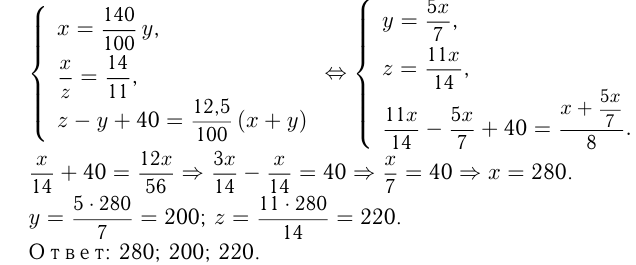
Задача №107
Определить целое положительное число по следующим данным: если к его цифровой записи присоединить справа цифру 4, получится число, делящееся без остатка на число, большее искомого на 4, а в частном получится число, меньшее делителя на 27.
Решение:
Пусть искомое число 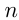 . При приписывании к нему справа цифры 4 получается число
. При приписывании к нему справа цифры 4 получается число 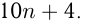 Из условия
Из условия
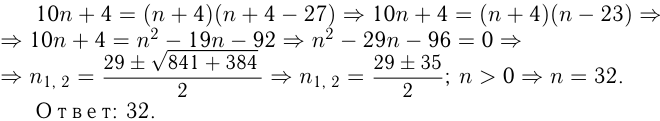
Задача №108
Даны два двузначных числа, из которых 2-е обозначено теми же цифрами, что и 1-е, но в обратном порядке. Частное от деления 1-го числа на 2-е равно 1,75. Произведение 1-го числа на цифру его десятков в 3,5 раза больше 2-го числа. Найти эти числа.
Решение:
Пусть 1-е число 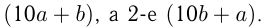 Тогда
Тогда
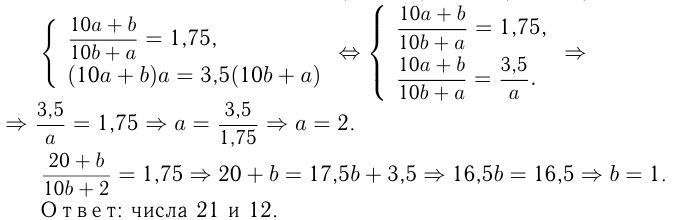
Задача №109
Было задано целое число. Требовалось увеличить его на 200 000 и полученное число утроить. Вместо этого приписали к цифровой записи числа справа цифру 2 и получили правильный результат. Какое число было задано?
Решение:
Допустим, было задано число 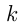 . Тогда
. Тогда
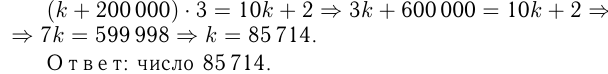
Задача №110
Найти два числа, сумма которых равна 44, причем меньшее число отрицательное. Процентное отношение разности между большим и меньшим числами к меньшему числу совпадает с меньшим числом.
Решение:
Обозначим числа 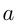 и
и 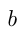 ,
, 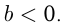 Из условий следует:
Из условий следует:
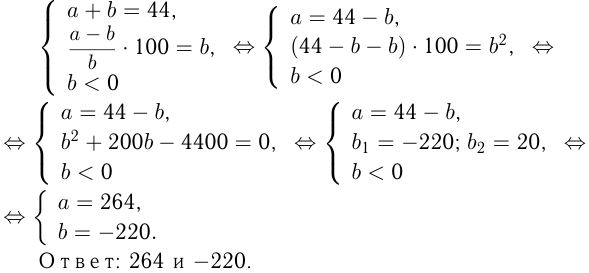
Задача №111
Если двузначное число разделить на сумму его цифр, то получится в частном 4 и в остатке 3. Если же это число разделить на произведение его цифр, то получится в частном 3 и в остатке 5. Найти это число.
Решение:
Пусть 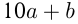 — двузначное число. Условия дают два уравнения:
— двузначное число. Условия дают два уравнения:
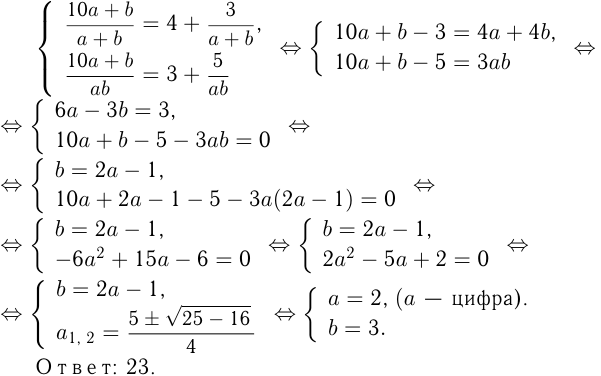
Задача №111
Однозначное число увеличили на 10. Если полученное число увеличить на столько же процентов, как в первый раз, то получится 72. Найти первоначальное число.
Решение:
Пусть 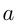 — первоначальное число,
— первоначальное число, 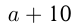 — увеличенное число. По условию:
— увеличенное число. По условию:
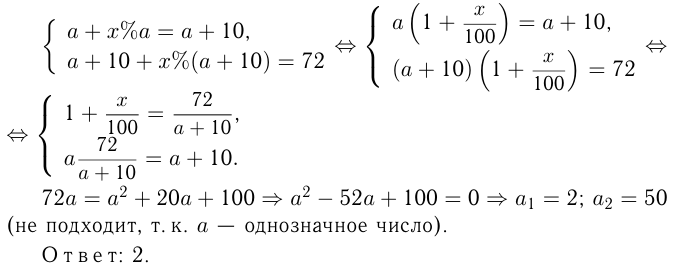
Задача №112
Найти четыре числа, образующих пропорцию, если известно, что сумма крайних членов равна 14, сумма средних членов равна 11, а сумма квадратов всех четырех чисел равна 221.
Решение:
Дано: 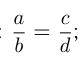
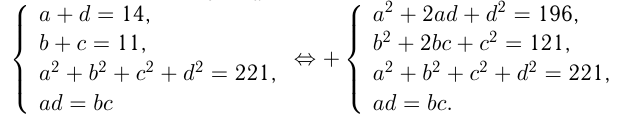

Задача №113
Запись шестизначного числа начинается цифрой 2. Если эту цифру перенести с 1-го места на последнее, сохранив порядок остальных цифр, то вновь полученное число будет втрое больше првоначального. Найти первоначальное число.
Решение:
Имеем число 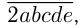 , где
, где 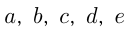 — цифры шестизначного числа, начиная со 2-й. Вновь полученное число будет
— цифры шестизначного числа, начиная со 2-й. Вновь полученное число будет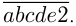 Обозначим число
Обозначим число 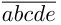 через
через 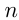 . Тогда первоначальное число
. Тогда первоначальное число 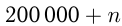 , а вновь полученное
, а вновь полученное 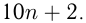 По условию
По условию
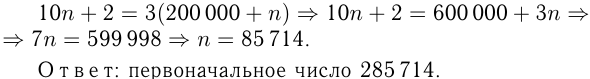
Задача №114
При умножении двух чисел, одно из которых на 10 больше другого, ученик допустил ошибку, уменьшив цифру десятков произведения на 4. При делении полученного произведения на меньший множитель для проверки ответа он получил в частном 39 и в остатке 22. Найти множители.
Решение:
Пусть ученик умножал числа 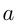 и
и 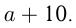 Можно записать:
Можно записать:
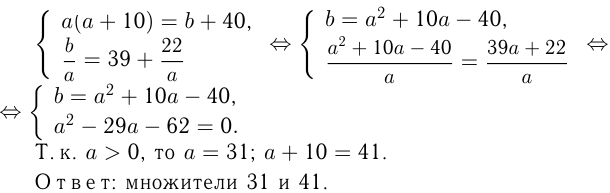
Этот материал взят со страницы решения задач по математике:
Возможно вам будут полезны эти страницы:
| Решение задач на работу по математике |
| Решение задач на части по математике |
| Решение задач с целочисленными неизвестными по математике |
| Решение задач с помощью неравенств |

