Оглавление:
Решение уравнений с помощью введения вспомогательного угла, методом замены неизвестного и разложения на множители, с помощью формул понижения степени
Справочные сведения
Метод введения вспомогательного угла.
Рассмотрим уравнение вида
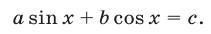
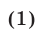
Будем считать, что  ,
, 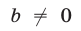 (в противном случае получаем простейшее тригонометрическое уравнение вида
(в противном случае получаем простейшее тригонометрическое уравнение вида 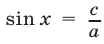 или
или 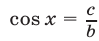 ).
).
Если 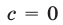 , то уравнение (1) является однородным и при
, то уравнение (1) является однородным и при  равносильно уравнению
равносильно уравнению 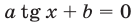 (см. §11).
(см. §11).
В §4 (пример 16) был изложен метод введения вспомогательного угла для преобразования выражения вида 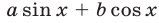 и было установлено, что
и было установлено, что
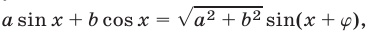
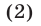
где 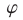 — такой угол, что
— такой угол, что
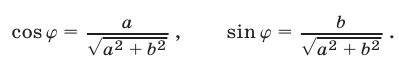
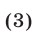
Используя (2), запишем уравнение (1) в виде 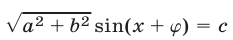
или
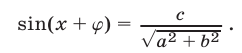
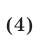
Уравнение (4) (и равносильное ему уравнение (1)) имеет корни
тогда и только тогда, когда 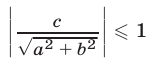 т. е.
т. е.
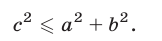
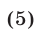
Если условие (5) выполнено, то уравнение (1) имеет следующие корни:
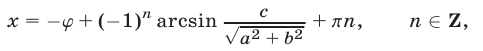
где 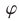 определяется формулами (3).
определяется формулами (3).
Если же условие (5) не выполнено, т. е. 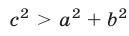 , то уравнение (1) не имеет корней.
, то уравнение (1) не имеет корней.
Метод замены неизвестного.
а) Замена 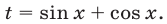 Если уравнение имеет вид
Если уравнение имеет вид
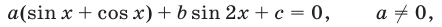
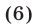
то, полагая 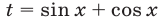 и учитывая, что
и учитывая, что
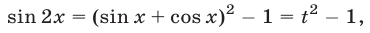
сведем уравнение (6) к квадратному уравнению вида
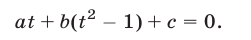
Уравнения вида
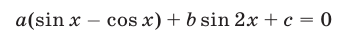
решаются аналогично с помощью подстановки 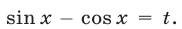 Эта же подстановка позволяет свести к алгебраическому уравнению уравнение вида
Эта же подстановка позволяет свести к алгебраическому уравнению уравнение вида
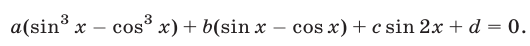
б) Замена 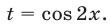 Такую замену можно применять при решении уравнений вида
Такую замену можно применять при решении уравнений вида
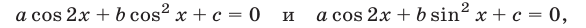
которые сводятся к простейшим тригонометрическим уравнениям вида 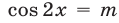 , если воспользоваться формулами удвоения аргумента
, если воспользоваться формулами удвоения аргумента
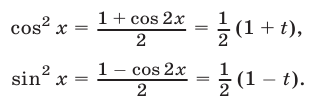
в) Замена 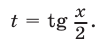 Если в тригонометрическом уравнении
Если в тригонометрическом уравнении 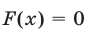 левая часть является рациональной функцией от
левая часть является рациональной функцией от 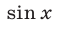 и
и 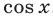 т.е. ее можно представить в виде
т.е. ее можно представить в виде 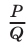 , где
, где 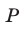 и
и  — многочлены от
— многочлены от 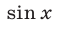 и
и 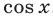 , то это уравнение сводится к алгебраическому уравнению относительно
, то это уравнение сводится к алгебраическому уравнению относительно 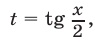 поскольку
поскольку
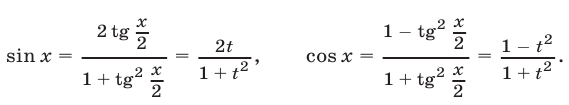
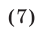
Однако следует иметь в виду, что использование подстановки 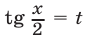 при решении тригонометрических уравнений часто приводит к трудной задаче нахождения корней многочлена степени
при решении тригонометрических уравнений часто приводит к трудной задаче нахождения корней многочлена степени  . Поэтому указанную подстановку, как правило, применяют лишь в том случае, когда не видно других путей решения уравнения.
. Поэтому указанную подстановку, как правило, применяют лишь в том случае, когда не видно других путей решения уравнения.
Отметим еще, что формулы (7) теряют смысл, если 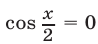 , т. е. если
, т. е. если 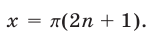 Поэтому при решении уравнений с помощью подстановки
Поэтому при решении уравнений с помощью подстановки 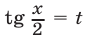 следует проверить, не являются ли значения
следует проверить, не являются ли значения 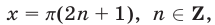 корнями исходного уравнения.
корнями исходного уравнения.
Метод разложения на множители.
Одним из наиболее употребительных методов решения тригонометрических уравнений является метод разложения на множители. Этим методом можно решать уравнения следующих видов:
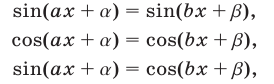
используя формулы разности (суммы) синусов или косинусов (см. формулы (15)-(18) из §4), а также некоторые уравнения вида
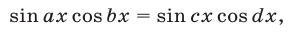
предварительно преобразовав произведения тригонометрических функций в суммы по формулам (21)—(23) из §4..
Использование формул понижения степени.
При решении тригонометрических уравнений находят широкое применение формулы понижения степени 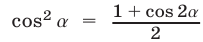 и
и 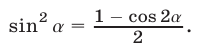
Примеры с решениями
Пример №119.
Решить уравнение 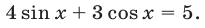
Решение:
Разделив обе части уравнения на 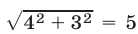 , получим равносильное уравнение
, получим равносильное уравнение
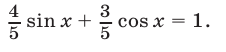
Пусть  — такой угол, что
— такой угол, что 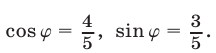 Так как
Так как 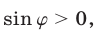
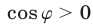 , то в качестве
, то в качестве 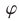 можно взять
можно взять 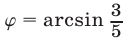 или
или 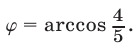 Получаем уравнение
Получаем уравнение 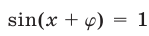 откуда
откуда 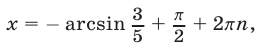
Пример №120.
Решить уравнение 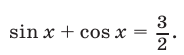
Решение:
Это — уравнение вида (1), в котором 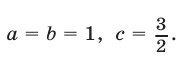 Так как
Так как 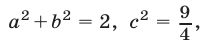 то
то 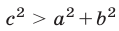 и поэтому уравнение не имеет корней.
и поэтому уравнение не имеет корней.
Пример №121.
Решить уравнение 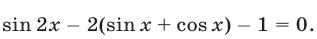
Решение:
Пусть 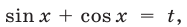 тогда
тогда 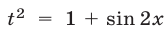 и уравнение можно записать в виде
и уравнение можно записать в виде  откуда
откуда 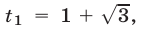
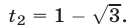
Если 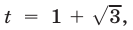 то
то 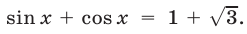 Это уравнение не имеет решений, так как
Это уравнение не имеет решений, так как 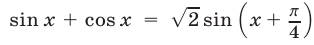 и поэтому
и поэтому 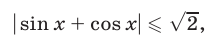 а его правая часть больше двух.
а его правая часть больше двух.
Если 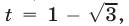 то получаем уравнение
то получаем уравнение 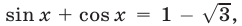 которое равносильно уравнению
которое равносильно уравнению
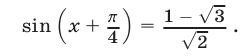
Так как 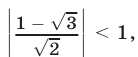 то это уравнение имеет корни, определяемые из равенства
то это уравнение имеет корни, определяемые из равенства
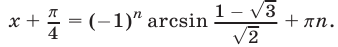
Ответ. 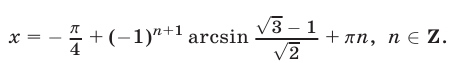
Пример №122.
Решить уравнение 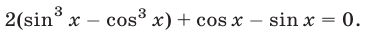
Решение:
Пусть 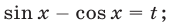 тогда
тогда
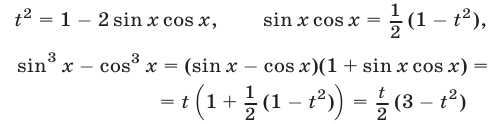
и данное уравнение примет вид
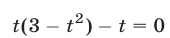 или
или 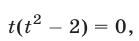
откуда 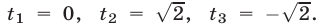 Поэтому исходное уравнение равносильно совокупности следующих трех уравнений
Поэтому исходное уравнение равносильно совокупности следующих трех уравнений
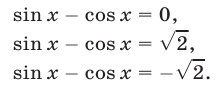
Первое уравнение, равносильное уравнению 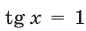 , имеет корни
, имеет корни 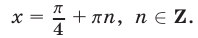
Второе уравнение можно записать в виде 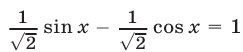 или
или 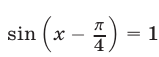 откуда
откуда 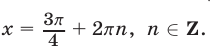 Аналогично, третье уравнение преобразуется к виду
Аналогично, третье уравнение преобразуется к виду 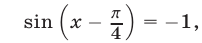 откуда
откуда 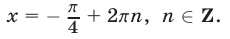
Ответ.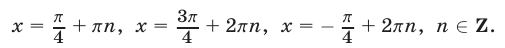
Пример №123.
Решить уравнение 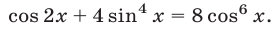
Решение:
Пусть 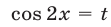 ; тогда
; тогда 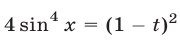 ,
, 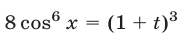 и уравнение примет вид
и уравнение примет вид
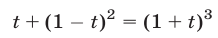 или
или 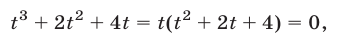 откуда получаем
откуда получаем 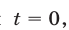 т. e.
т. e. 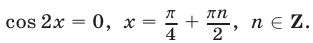 Уравнение
Уравнение 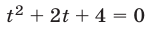 не имеет действительных корней.
не имеет действительных корней.
Ответ. 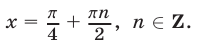
Пример №124.
Решить уравнение 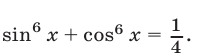
Решение:
Это уравнение можно решить с помощью замены 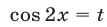 , записав его в виде
, записав его в виде 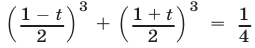 , или после упрощений, в виде
, или после упрощений, в виде 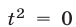 . Итак,
. Итак, 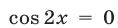 , откуда
, откуда 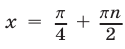 ,
, 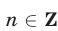 .
.
Замечание. Воспользовавшись равенством 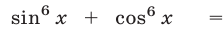
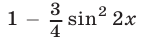 (§4, пример 4,6), можно преобразовать уравнение к виду
(§4, пример 4,6), можно преобразовать уравнение к виду 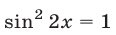 или
или 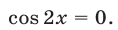
Пример №125.
Решить уравнение 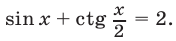
Решение:
Заметим, что значения 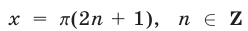 не являются корнями исходного уравнения. Воспользуемся подстановкой
не являются корнями исходного уравнения. Воспользуемся подстановкой 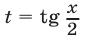 и запишем уравнение в виде
и запишем уравнение в виде 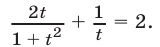
Так как числа 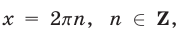 являющиеся корнями уравнения
являющиеся корнями уравнения 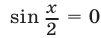 , не удовлетворяют исходному уравнению, то
, не удовлетворяют исходному уравнению, то 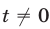 . Поэтому полученное нами алгебраическое уравнение равносильно уравнению
. Поэтому полученное нами алгебраическое уравнение равносильно уравнению 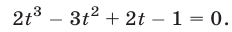
Преобразуем это уравнение, учитывая, что 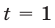 —его корень. Получим
—его корень. Получим
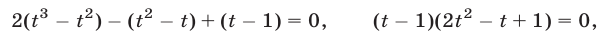
откуда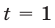 , т. e.
, т. e. 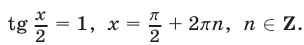
Ответ. 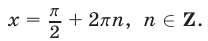
Пример №126.
Решить уравнение 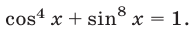
Решение:
С помощью подстановки 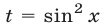 уравнение приводится к алгебраическому уравнению
уравнение приводится к алгебраическому уравнению 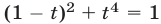 , которое равносильно каждому из уравнений
, которое равносильно каждому из уравнений
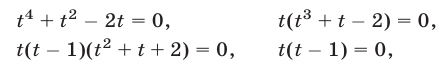
откуда находим 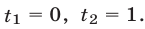 Если
Если 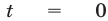 , то
, то  ,
, 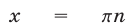 . Если
. Если 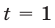 , то
, то 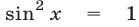 ,
, 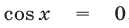 ,
, 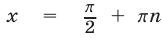 . Полученные серии корней можно объединить в одну:
. Полученные серии корней можно объединить в одну: 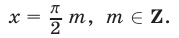
Ответ. 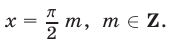
Пример №127.
Решить уравнение 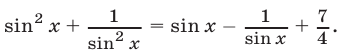
Решение:
Пусть 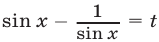 тогда
тогда 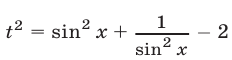 и уравнение преобразуется к виду
и уравнение преобразуется к виду 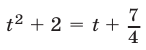 , или
, или 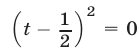 , откуда
, откуда 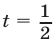 ; т. е.
; т. е.
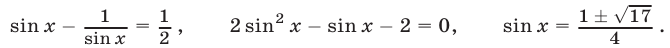
Так как уравнение 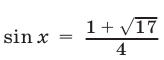 не имеет корней, то исходное уравнение равносильно уравнению
не имеет корней, то исходное уравнение равносильно уравнению 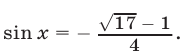
Ответ. 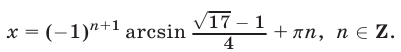
Пример №128.
Решить уравнение
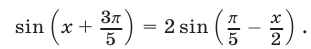
Решение:
Положим 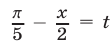 ; тогда
; тогда 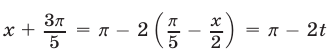
и уравнение примет вид
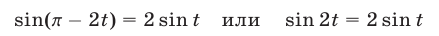
или
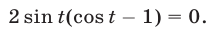
Так как корни уравнения 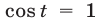 содержатся среди корней уравнения
содержатся среди корней уравнения 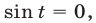 то исходное уравнение равносильно уравнению
то исходное уравнение равносильно уравнению 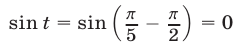 , откуда
, откуда 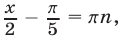
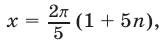
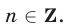
Ответ. 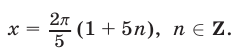
Пример №129.
Решить уравнение 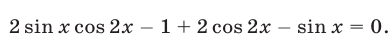
Решение:
Вынося общий множитель первого и третьего слагаемых, запишем уравнение в виде
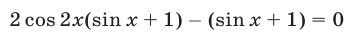 или
или 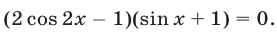
Исходное уравнение равносильно совокупности двух уравнений: 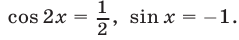
Ответ. 
Пример №130.
Решить уравнение 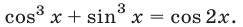
Решение:
Левая и правая части уравнения имеют общий множитель 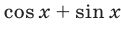 , так как
, так как
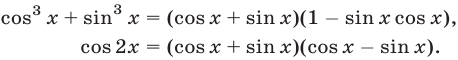
Поэтому исходное уравнение, записанное в виде
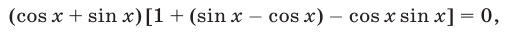
равносильно совокупности двух уравнений:
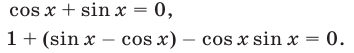
Первое уравнение имеет корни 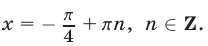 Второе уравнение заменой
Второе уравнение заменой 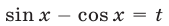 приводится к уравнению
приводится к уравнению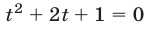 откуда
откуда 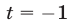 , т.е.
, т.е. 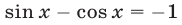 или
или
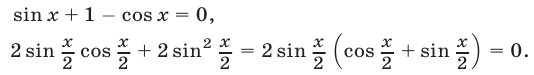
Если 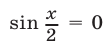 , то
, то 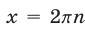 , а если
, а если 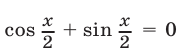 , то
, то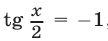 , откуда
, откуда 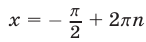
Ответ. 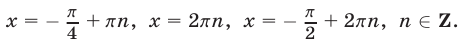
Пример №131.
Решить уравнение 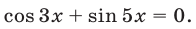
Решение:
Используя формулу 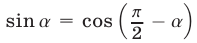 и формулу суммы косинусов, преобразуем данное уравнение:
и формулу суммы косинусов, преобразуем данное уравнение:
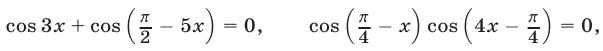
Пример №132.
Решить уравнение 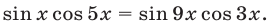
Решение:
Преобразуя произведения тригонометрических функций в сумму (разность) с помощью формулы (21) из §4, запишем уравнение в виде
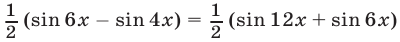 или
или 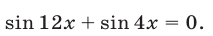
Разложим левую часть этого уравнения на множители, применив формулу суммы синусов:
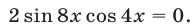
Так как 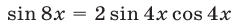 , то исходное уравнение можно заменить равносильным уравнением
, то исходное уравнение можно заменить равносильным уравнением 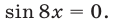
Ответ.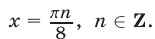
Пример №133.
Решить уравнение
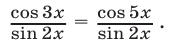
Решение:
Уравнение равносильно каждому из следующих уравнений:
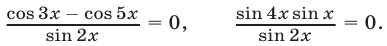
Так как 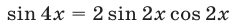 , а ОДЗ уравнения определяется условием
, а ОДЗ уравнения определяется условием 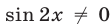 , то
, то 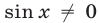 , и исходное уравнение равносильно уравнению
, и исходное уравнение равносильно уравнению 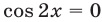 .
.
Ответ. 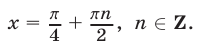
Пример №134.
Решить уравнение 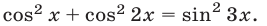
Решение:
Преобразуем левую часть уравнения, используя формулу 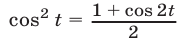 суммы косинусов. Получим
суммы косинусов. Получим
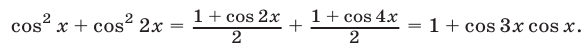
Исходное уравнение равносильно каждому из уравнений
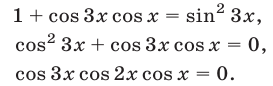
Следовательно, оно равносильно совокупности трех уравнений:
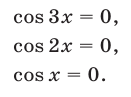
Корнями первого из них являются числа 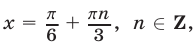 а корнями второго — числа
а корнями второго — числа 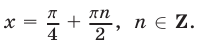 Корни уравнения
Корни уравнения 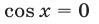 содержатся среди корней уравнения
содержатся среди корней уравнения 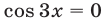 .
.
Ответ. 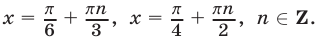
Пример №135.
Решить уравнение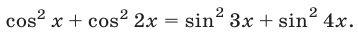
Решение:
Используя формулы 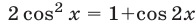 ,
, 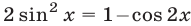 , а так же формулу суммы косинусов, последовательно преобразуем данное уравнение:
, а так же формулу суммы косинусов, последовательно преобразуем данное уравнение:
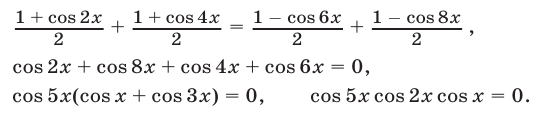
Заметим, что все корни уравнения 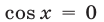 содержатся среди корней уравнения
содержатся среди корней уравнения 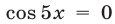 . Действительно, если
. Действительно, если 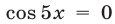 , то
, то 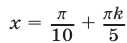 . Полагая
. Полагая 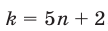 , получаем
, получаем 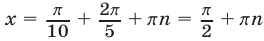 .
.
Следовательно, исходное уравнение равносильно совокупности уравнений 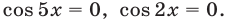
Ответ. 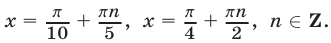
Пример №136.
Решить уравнение
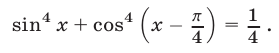
Решение:
Применяя формулы понижения степени, запишем уравнение в виде
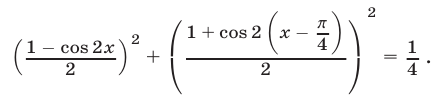
Исходное уравнение равносильно каждому из следующих уравнений :
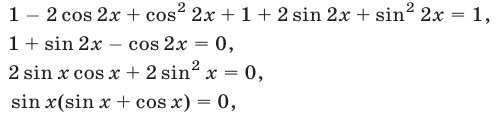
откуда находим 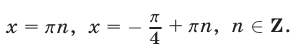
Ответ. 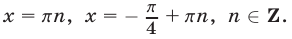
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Возможно вам будут полезны эти страницы:

