Решение уравнений

Решение уравнений

Решение уравнений. Для решения уравнений. ！(х)=0.(60.9)） Если функция / непрерывна в интервале[a, b]и принимает значения различных знаков на обоих концах отрезка, то метод, с помощью которого доказывается теорема в§ 6.2 относительно существования точки X0, в которой функция исчезает, в этом случае также дает приближенное выражение method. To для этого достаточно последовательно разделить отрезки[a, b]пополам. Каждый раз функция / выбирает сегмент, который принимает другое значение знака(если, конечно, функция / не исчезает в 1 конце результата), если нужный маршрут уже найден).Если необходимо найти корень уравнения к заданному е 0 (60.9), то после n-го шага (слева-и недостаток, справа-избыток) так, чтобы конец полученного отрезка давал искомое приближение некоторого корня уравнения (60.9).

By закон постоянства первой производной функции f является строго монотонным. следовательно, при сделанных предположениях уравнение (60.9) имеет 1 корень строго в интервале(a, b). Людмила Фирмаль

• Приближенное решение этого уравнения(60.9), называемое «методом вилки», в принципе очень простое, но очень laborious. In в большинстве случаев он используется только для «грубой оценки» результатов. То есть он используется для»грубого»определения интервала, в котором присутствуют искомые корни рассматриваемого уравнения, а затем в этом интервале используются другие более быстрые методы сходимости для поиска более точных значений корней; обычно используется тангенциальный метод, описанный ниже («метод Ньютона«).Аналогично,§ 60.Некоторые вопросы приблизительного расчета Пятьсот сорок восемь Согласно этой схеме, он работает медленно при выполнении вычислений на быстром компьютере.

Конечно, этот метод также рекомендуется, особенно при выполнении расчетов «вручную», с помощью скользящей линейки или мини-компьютера. Рассмотрим, как решить уравнение. Это называется методом кода и методом касательной. Последний из них хорошо обобщен в случае системы уравнений. Ниже мы всегда предполагаем, что функция[непрерывна в интервале[a, b], имеет производные первого и второго порядкав этом интервале, и оба являются знаковыми константами (особенно ненулевыми). Также предположим, что функция/принимает различное значение знака на обоих концах segment.

• Кодовый метод Метод заключается в следующем: функция / график заменяется сегментом, соединяющим его хорды, то есть конечной точкой функции/графика. Пункты (a, [(a)) и (b, f (6)).Абсцисса X1 точка. Пересечение этого кода с осью Ox считается первым приближением искомого маршрута (рис. 234).Затем возьмем 1 из отрезков[a, X1]и(xb 6]. в его конце функция / принимает значение другого знака(в предположении f (x.)^ = 0, следовательно, такой отрезок всегда присутствует), и к нему применяется тот же метод;2-е приближение корня x1 получается, в результате получается последовательность xn, n = 1, 2…It будет formed. To корень уравнения (60.9). Легко получить повторяющееся выражение для заданного числа xn, n = 1, 2 уравнение прямой через экстремум Точки функции / графика имеют формат (60.10)） г ^ ФИМ (x_a)+!{ля).

В методе аккордов достаточно требовать существования 1-й и 2-й производных только на интервале (a, b).60.2.Решение уравнения Пятьсот сорок девять Представляет правую сторону с I (x).То есть напишите формулу (60.10) в виде: У = ТХ). Х1 = аЭто легко проверить Ф-а) [(а) 1Ф) −1 (а) ’ И xx в (60.11） (60.12） Найти абсциссу XI для пересечения прямой (60.10) и оси Ox. То есть мы решаем уравнение 1(x) 0.Мы получаем (Например, это основано на точной монотонности и непрерывности функции 1 (x) и на том, что в конце интервала[a, d]принимают значения различных знаков. I (a)=-/(a) и Ir)=1Φ)) аналогично、 ху + 1 = СА-(б-х ^ м ^, п = 1,2,….(60.13).

Существование производных на концах отрезков [a, b] используется только в касательном методе. Людмила Фирмаль

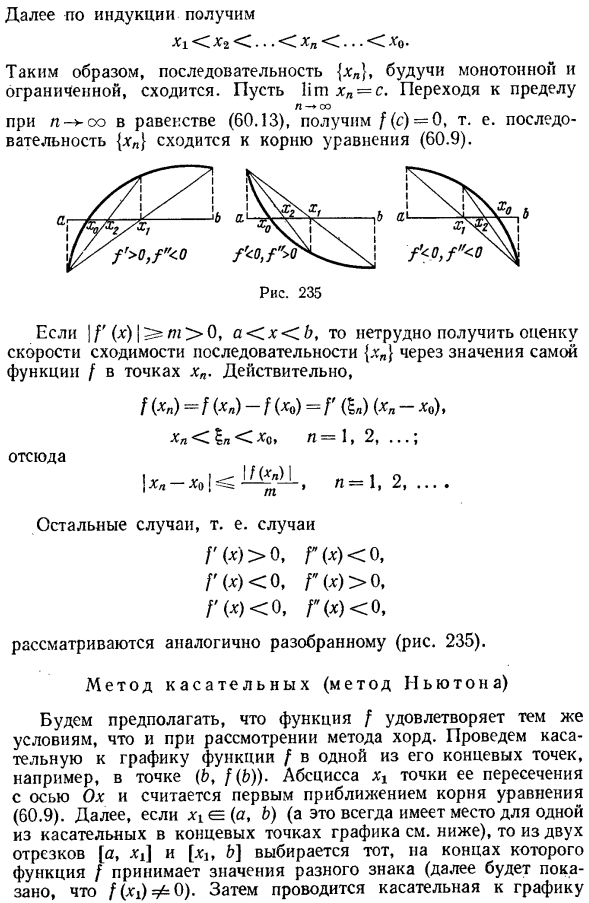
• Указывает, что последовательность{xn}стремится монотонно стать корнем уравнения (60.9). для уточнения,/’.(X) 0, {«(x) 0 и x .предположим, что b (см. рис. 234). в этом случае функция / строго монотонно возрастает и строго under-convex. So, внутренняя точка кода, соединяющая крайние точки графа функции/, находится выше соответствующей точки графа функции/. 1 (x)} (x) и xcb. Особенно если x0-корень уравнения(60.9). /(x0)= 0, то Я(х0) 0. (См. (60.11) и (60.12)). Я(*!) = 0, и x1Cb. Подобный этому 1(Х1)1(Х0),(60.14） Но линейная функция I (x) возрастает строго монотонно. Ь)=Ь))=а) следовательно (60.14） ХХ х0. Если вы замените сегмент[a, b]на сегмент [xi b] и обратите внимание на^ x.) 0, это также доказано. Х2.Эй. § 60.Некоторые вопросы для приблизительной оценки Пятьсот пятьдесят Кроме того, индуктивным методом、 * 1 Х2. * ■ * » … * Идти Таким образом, последовательный.

Смотрите также:

Решение задач по математическому анализу

Преобразование Фурье обобщенных функций.	Интерполяция функций.
Применение формулы Тейлора для приближенного вычисления значений функций и интегралов.	Квадратурные формулы.