Оглавление:
Решение систем линейных уравнений. Теорема Кронекера-Капелли
Пусть дана произвольная система 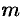 линейных уравнений с
линейных уравнений с 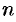 неизвестными
неизвестными
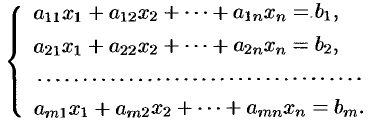
Исчерпывающий ответ па вопрос о совместности этой системы дает теорема Кронекера-Капелла.
Теорема 4.1. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.
Примем ее без доказательства.
Правила практического разыскания всех решений совместной системы линейных уравнений вытекают из следующих теорем.
Теорема 4.2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема 4.3. Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
Правило решения произвольной системы линейных уравнений
- Найти ранги основной и расширенной матриц системы. Если
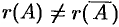 , то система несовместна.
, то система несовместна. - Если
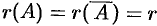 , система совместна. Найти какой-либо базисный минор порядка г (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять
, система совместна. Найти какой-либо базисный минор порядка г (напоминание: минор, порядок которого определяет ранг матрицы, называется базисным). Взять 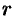 уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные
уравнений, из коэффициентов которых составлен базисный минор (остальные уравнения отбросить). Неизвестные, коэффициенты которых входят в базисный минор, называют главными и оставляют слева, а остальные 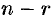 неизвестных называют свободными и переносят в правые части уравнений.
неизвестных называют свободными и переносят в правые части уравнений. - Найти выражения главных неизвестных через свободные. Получено общее решение системы.
- Придавая свободным неизвестным произвольные значения, получим соответствующие значения главных неизвестных. Таким образом можно найти частные решения исходной системы уравнений.
Пример №4.1.
Исследовать на совместность систему
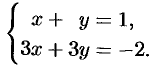
Решение:
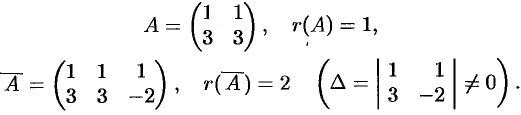
Таким образом, 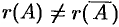 , следовательно, система несовместна.
, следовательно, система несовместна.
Дополнительный пример №4.2.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Свойства определителей |
| Невырожденные матрицы |
| Решение невырожденных линейных систем |
| Решение систем линейных уравнений методом Гаусса |

