Решение систем линейных уравнений. теорема Кронекера-Капелли

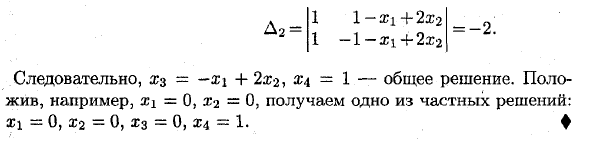
Решение систем линейных уравнений. теорема Кронекера-Капелли

• Решение системы линейных уравнений. Теорема Кронекера Капелли дать произвольную систему из m линейных уравнений с n неизвестными 0. \ X \ + «12 ^ 2 + ••• + a \ nXn = 6b a2 \ Xi + CI22X2 n —— 1-> 0 Я k am \ X \ -f am2X2 H —— h amnnn = bm. Комплексный ответ на этот вопрос совместимости системы дается теоремой Кронекера-Капсулы. Теорема 1. Система линейных алгебраических уравнений совместима только в том случае, если ранг матрицы расширения системы равен рангу главной матрицы.

Принять без доказательств. Практическое правило поиска для всех решений линейных систем дается следующей теоремой. Теорема 2. Теорема 3. Если ранг связанной системы меньше числа неизвестных, система имеет бесчисленные решения.

Если ранг связанной системы равен числу неизвестных, система имеет единственное решение. Людмила Фирмаль

Правила решения любой системы ( Линейное уравнение Найти ранг главной и расширенной матриц системы. Для r (A) Φr (A) система несовместима. 2. Если r (A) = r (A) = r, система совместима. Найдите базового майнера порядка r (примечание: майнер, порядок которого определяет ранг матрицы, называется базой).

Возьмите r уравнений из коэффициентов, составляющих основной минор (отбросьте остальные уравнения). Неизвестные, коэффициенты которых содержатся в основном миноре, называются основными, остаются слева, а остальные n-r неизвестные называются свободными и переносятся в правую часть уравнения.

• Следуйте правилам Крамера (или методу Гаусса), чтобы найти основные неизвестные выражения из свободных. Получено общее решение для системы. 4. Приведите любое значение свободному неизвестному и получите соответствующее значение основного неизвестного. Следовательно, вы можете найти конкретное решение исходной системы уравнений.

Пример: х + у = 1 1) Проверьте совместимость системы 3х + 3 года = -2. г (А) = 1 ‘1 G 3 3 A = ‘1 1 3 3 1-2 r (A) = 2 D = A = № 0 Следовательно, r (A) Φr (A) и, следовательно, система не совместима. ♦ 2) Решить систему X1-2X2 + S3 + £ 4 = 1, X1-2X2 + X3-X4 = -1, X1-2X2 + X3 + 3X4 = 3. ♦ g (A) -g (A) = 2. Возьмите первые два уравнения. xi-2х-2х3 + х4t = I, xi -2×2 + ‘ХЗГ ~ _? 4 J = -l • X3 ^ X4 = 1-X1 + 2X2, X3-X4 = -1-X \ — \ — 2×2 • д = Ai = = -2 ^ 0, 1-371 + 2X2 1 -1-? Я + 2х2 -1 1 1 1 -1 = 2xi-4×2 1 1-а? 1 + 2®2 1 —1 — XI + 2X2 d2 = = -2 Следовательно, x $ = —X \ 4-2 ^ 2, x \ = 1 — общее решение.

Например, если x ± = 0 и x2 = 0, вы получите одно из конкретных решений. xi = 0, R2 = 0, x3 = 0, X4 = 1. Людмила Фирмаль

Смотрите также:

Предмет высшая математика

Системы линейных уравнений (основные понятия)	Точки и координаты
Решение невырожденных линейных систем. формулы крамера	Линии и уравнения