Оглавление:
Решение первой основной задачи динамики точки
К первой основной задаче динамики точки откосятся, как мы знаем, задачи, в которых по известному движению материальной точки требуется определить действующие на нес силы.
Если ускорение точки в данный момент известно, то действующая на нее сила находится сразу по основному уравнению (106) динамики точки.
Если движение точки задано координатным или естественным способом, то сначала находятся по уравнениям (111) или (112) проекции силы, соответственно на оси декартозых или естественных координат, а затем уже модуль и направление силы.
Сели точна несвободная, т.е. если па нее наложены связи, ограничивающие движение точки, то при решении задач динамики пользуются известным еще из статики принципом освобождаемости.
Мысленно отбрасывая связи, заменяют их действие на точку реакциями этих связей и рассматривают точку как свободную, совершающую движение под действием приложенных к ней активных сил и реакций связей.
Для несвободной точки основное уравнение динамики можно записать, следовательно, в виде
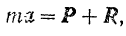
где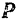 
— равнодействующая всех активных сил, приложенных к точке, 
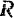— равнодействующая реакций наложенных на точку связей.
В соответствии с уравнением (106′) в случае несвободной точки в правую часть уравнений (111) и (112) будут также входить и проекции на соответствующие оси реакции связей.
Если точка несвободна, то первая задача динамики обычно сводится к тому, чтобы, зная движение точки и действующие на нее активные силы, определить реакции наложенных на точку связей.
Пример задачи:
Материальная точка весом
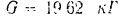
движется прямолинейно и равномерно ускоренно. За 8 сек., скорость точка изменилась от 10 м/сtк до 50 м/сек. Определить равнодействующую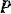 
сил, действующих на точку.
Решение:
Ускорение прямолинейного равномерно ускоренно:о движения точки
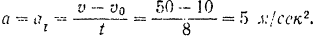
Модуль силы, действующей на точку, равен
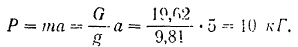
Так как при прямолинейным равномерно переменном движении точки
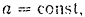
то и сила
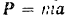
будет постоянной как по модулю, так и по направлению.
Пример задачи:
Материальная точка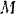 
массы 
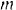движется в плоскости 
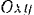согласно уравнениям
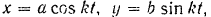
где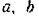 
и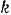 
— постоянные ветчины. Определить силу 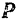. вызывающую данное движение точки.
Решение:
На основании дифференциальных уравнений (111) движения точки проекция силы на ось абсцисс:
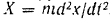
В данном случае
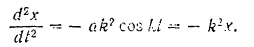
Следовательно,
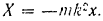
Аналогично,
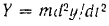
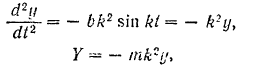
Вектор силы
Так как радиус-вектор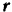 
точки 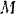равен
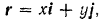
то вектор силы
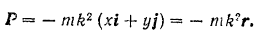
Следовательно, сила 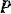равна по модулю
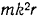
и направлена противоположно радиусу-вектору 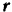, т. е. от точки 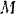к точке 
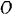(рис. 161).
Заданные уравнения движения точки являются параметрический уравнениями эллипса, с полуосям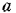и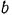 
и 
и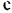 
центром и точке .
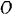Таким образом, точка 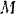движется по эллипсу под действием силы 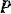притяжения к его центру.
Пример задачи:
Груз 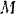, подвешенный на нити 
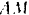в неподвижной точке 
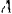, представляет собой коническим маятник, т. е. описывает окружность в горизонтальной плоскости (рис. 165). Определить реакцию 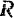нити и угол а, составляемый нитью с вертикальной, если расстояние точки 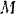от начала 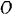отсчета изменяется по закону
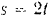
Вес груза
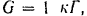
длина нити
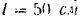
Решение:
Принимаем груз за материальную точку 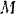На нее действуют силы: активная
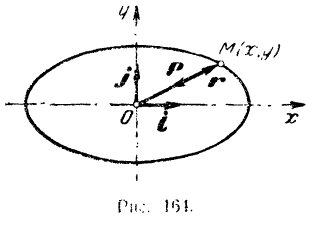
Проектируя приложенные к точке 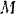силы на оси естественных координат, получим:
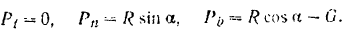
Из условий задачи имеем
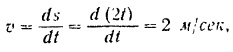
откуда
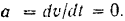
Радиус кривизны окружности
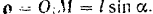
Следовательно, уравнения движения данной точки приводятся к виду:
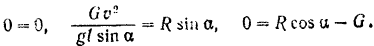
Из последнего уравнения имеем
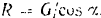
Подставляем найденное значение для 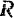во второе из уравнений,
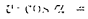
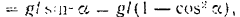
откуда
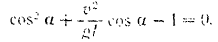
Решая последнее уравнение и подставляя числовые данные находим
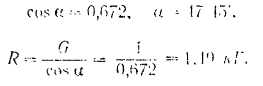
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
