Оглавление:
Решение определенных линейных систем алгебраических уравнений (1.10) можно получить с помощью правила Крамера. Обозначим определитель (детерминант) матрицы системы 
символом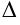 
(дельта — греческий алфавит):
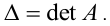
Сформулируем правило Крамера в применении к системам уравнений третьего порядка:
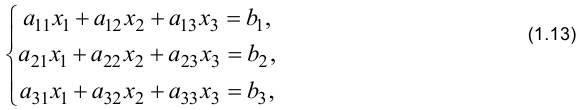
Правило Крамера
1) система (1.13) имеет единственное решение, если определитель матрицы системы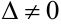 
;
2) само решение определяется по формулам Крамера
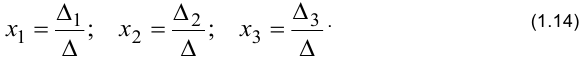
Определитель 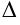составляется из коэффициентов при неизвестных, вспомогательные определители 
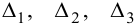получаются из определителя 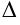путём замены первого, второго и третьего столбцов столбцом свободных членов:
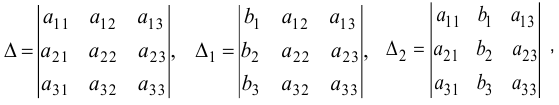
Пример:
Дана система линейных алгебраических уравнений:
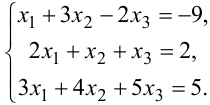
Доказать единственность её решения и найти это решение по формулам Крамера.
Решение:
Вычислим определитель системы:
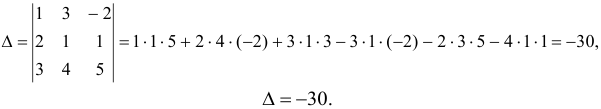
Так как 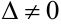, система имеет единственное решение. Для нахождения этого решения по формулам Крамера вычислим вспомогательные определители:
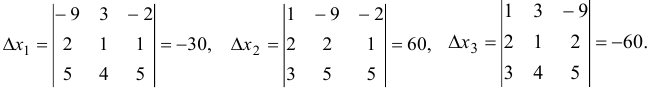
Подставляя значения полученных определителей в формулы (1.14), получаем решение системы:
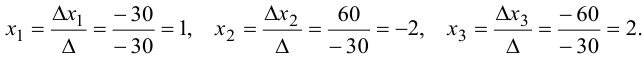
Эта лекция взята с этой страницы, там вы найдёте все темы лекций по высшей математике для студентов 1 курса:
Возможно вам будут полезны эти страницы:
