Оглавление:

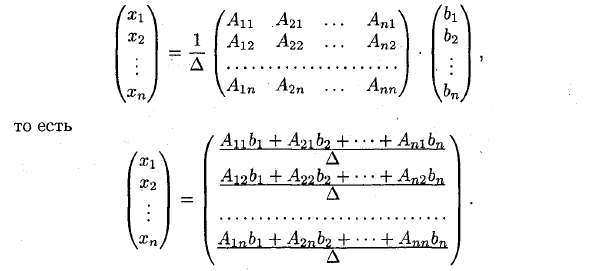

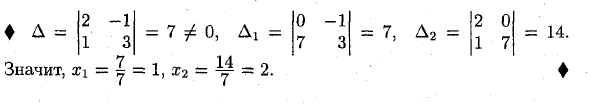

Решение невырожденных линейных систем. формулы крамера
- Неденатурирующее линейное системное решение. Формула Крамера дать систему из n линейных уравнений с n неизвестными тревога + <312X2 N —- + ainXn = 021X1 + 022 ^ 2 + ••• + a2n ^ n = aniXi + an2x2 H —— h annxn = 6n Или матричная форма A • X = B. Базовая матрица A такой системы является квадратной. Детерминанты этой матрицы ac … Ain D = Onru стр Это называется системным определителем.
Если определитель системы ненулевой, то система называется невырожденной. Для DΦ0 найдите решение этой системы уравнений. Умножение матрицы A с обеих сторон уравнения A-X = B дает «1, A» 1 • A • X = A’1 • B. A «1-A = EiE-X = X, поэтому (1) X = A’1 • B. Нахождение решения системы по уравнению (1) называется матричным методом решения системы. Опишите матричное уравнение (1) в следующем формате:l „l LL »« • a • Mi .l21 ^ 12 м2 • a • «» «I 4 *» X2 Vnj d \ Бн / Это / x2 \ X2 \ XnJ нн / Д • т L711 4- L2262 + ••• + An2bn Alnb \ + t ‘•• 4- Annbn
- = Anbl + L21 & 2 + — + Ambn d ^ nn ^ n Xp D Но Ambi + A21 & 2 H —— b ^ ni ^ n является детерминантом разложения bi «12 ••. Ain Dx = h 0-22 • 0-2 p bn aP2. Q-пп По первому элементу столбца. Определитель Dx получается из определителя D путем замены первого столбца коэффициентов на столбец свободных членов.
Почему. х \ = Аналогично: x2-Dg получается из D путем замены второго столбца коэффициентов на столбец свободных членов. Да_дп хз = D д • (2) Пример: решить систему xn = формула О! ; = -d, r = 1, n Это называется формула Крамера. Таким образом, невырожденная система из n линейных уравнений с n неизвестными имеет единственное решение, которое можно найти в матричном методе (1) или уравнении Крамера (2). 2xi-x2 = 0, xi + 3l2 = 7. X = 7 ^ 0, Ai = 2 -1 1 3 _ 7, „_ 14 _ Около 7 -1 3 2 0 1 7 ♦ A = = 7, A2 = = 14
Следовательно, Xi = j = 1, x2 = y = 2. Людмила Фирмаль
Смотрите также:
| Ранг матрицы | Решение систем линейных уравнений. теорема Кронекера-Капелли |
| Системы линейных уравнений (основные понятия) | Точки и координаты |

