Оглавление:
Решение невырожденных линейных систем. Формулы Крамера
Пусть дана система 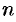 линейных уравнений с
линейных уравнений с 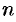 неизвестными
неизвестными
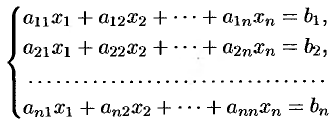
или в матричной форме 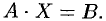
Основная матрица 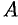 такой системы квадратная. Определитель этой матрицы
такой системы квадратная. Определитель этой матрицы

называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.
Найдем решение данной системы уравнений в случае 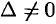 .
.
Умножив обе части уравнения 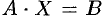 слева на матрицу
слева на матрицу 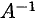 , получим
, получим 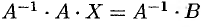 . Поскольку
. Поскольку 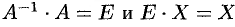 , то
, то

Отыскание решения системы по формуле (4.1) называют матричным способом решения системы.
Матричное равенство (4.1) запишем в виде

то есть
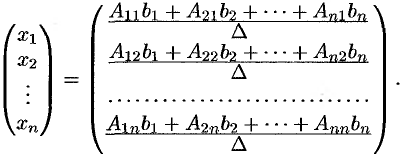
Отсюда следует, что
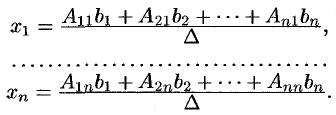
Но 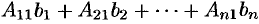 есть разложение определителя
есть разложение определителя

по элементам первого столбца. Определитель 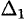 получается из определителя
получается из определителя  путем замены первого столбца коэффициентов столбцом из свободных членов.
путем замены первого столбца коэффициентов столбцом из свободных членов.
Итак, 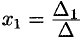
Аналогично: 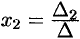 , где
, где 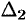 получен из
получен из  путем замены второго столбца коэффициентов столбцом из свободных членов;
путем замены второго столбца коэффициентов столбцом из свободных членов; 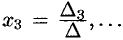
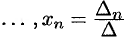 .
.
Формулы

называются формулами Крамера.
Итак, невырожденная система 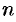 линейных уравнений с
линейных уравнений с 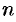 неизвестными имеет единственное решение, которое может быть найдено матричным способом (4.1) либо по формулам Крамера (4.2).
неизвестными имеет единственное решение, которое может быть найдено матричным способом (4.1) либо по формулам Крамера (4.2).
Пример №4.3.
Решить систему 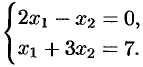
Решение:
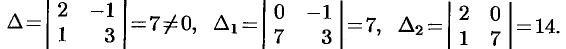
Значит, 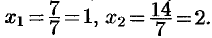
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Невырожденные матрицы |
| Решение систем линейных уравнений |
| Решение систем линейных уравнений методом Гаусса |
| Уравнения поверхности в пространстве |

