Рассмотрим решение квадратных уравнений, дискриминант которых отрицателен:
Пример №42.4.
Решить уравнение: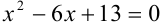 
.
Решение:
Найдем дискриминант: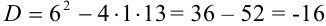 
.
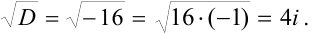
Тогда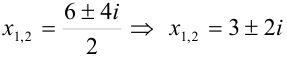 
.
Ответ: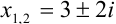 
.
Видим, что если дискриминант квадратного уравнения отрицателен, то уравнение имеет решения на множестве комплексных чисел. В ответе получаются два сопряженных комплексных числа. Это очень важный результат: теперь мы знаем, что абсолютно любое квадратное уравнение имеет два корня на множестве комплексных чисел.
Подобное утверждение, известное под названием «основная теорема алгебры», было доказано Гауссом в конце XVIII века: любое алгебраическое уравнение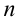 
-й степени имеет 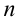комплексных корней (при этом некоторые корни являются кратными). Эти результаты подчеркивают ту исключительную роль, которую играют комплексные числа в теории алгебраических уравнений.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Алгебраическая форма комплексного числа. |
| Действия над комплексными числами в алгебраической форме. |
| Геометрическая интерпретация комплексных чисел. |
| Понятие модуля и аргумента комплексного числа. |
