Оглавление:



Решение Даламбера и Эйлера.
- Решение д’Аламбера и Эйлера. Эти ученые и впервые сформулировали эксплицитно Формулу(2). Его общее решение обоих из них-сначала Д’Аламбера (1747), затем Эйлера (1748)-представлено в
таком виде: (H). (6) 426ЧАП. XXIV. ряд Фурье[420 9 (I) и f (t? Функция » any » определяет все аргументы значения. Для наших целей
формула (6) для всех значений x и I должна удовлетворять условию (2), Каким Людмила Фирмаль
бы ни было d функций W d S d и f f e R e N C и R u e m s E функций (RIF). Возникает вопрос о выборе этих функций, чтобы также соблюдались ограничения и начальные условия.)] ? (Х)=Ф(Х)) (О^х^/). (V/)+f (- A1) -0,+
— AO=0 (^0) (For) и[см.(4)] ) (+?(- * ) =Ох, (7) * ) Всегда можно реализовать это равенство, если вычесть из<p и добавить y C к f, не теряя общности. (х^О. ) Тонны (/+х)+? (/- х)=0. (8) сначала определите
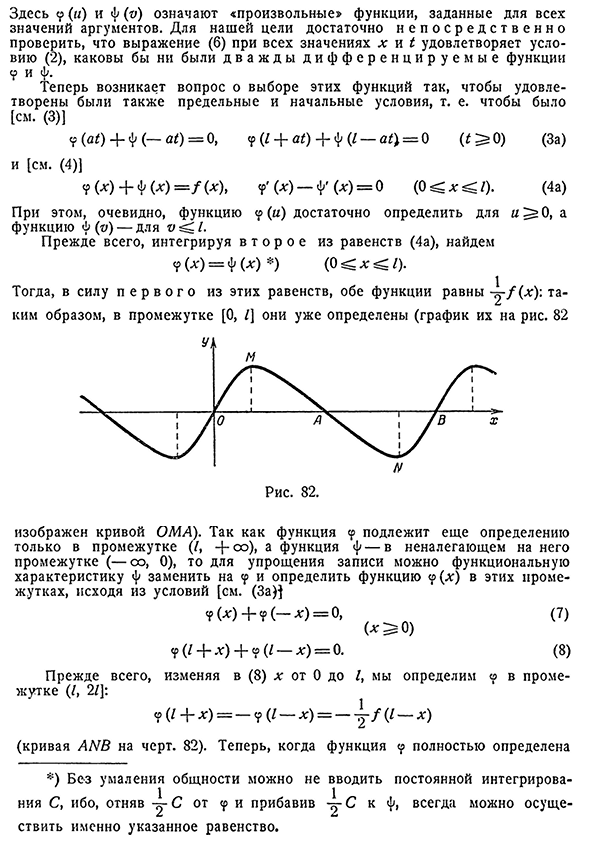
- интервал (/, 2), изменив x с (8)На / от 0/]: < ? (/+х)= -<? (/- x)= — f/ (/- x) (кривые A и B на прямой. 82). Поскольку функция была полностью определена, 4211§5. Очерк по истории тригонометрических функций серия 427 Благодаря интервалу[0, 2/] и-(5A) — далее<p(0)=<? (2/)=O,
докажите, что он имеет N E R и O d2 / вообще, и определите его во всех интервалах(—OO,+OO). Сначала ставим 6^ -/; (8) x=^+/, затем учитываем [(7)]<p (^+2/)= -? (-6)? (Позже.) Аналогично, для-I возьмем (8) x=—(&0 и [снова полагаемся на (7)]. В общем случае в виде графика функции y мы получаем «серпантинную кривую»
(в уравнении Эйлера), показанную на рисунке. 82 она должна быть симметричной Людмила Фирмаль
относительно начала, так как функция (7)<p (x) n E h t n A I. Поскольку функция/(x)имеет две производные в интервале[0,/]и удовлетворяет условиям(5A) и(56), то функция(x), определенная таким образом, имеет точку вида k1(y).= 0, ± 1 , ± 2 , …), Отдельные части кривой «слипаются». С помощью этой функции желаемое решение окончательно указывается в виде Пять. 1=< п (х+а/)+<р(х-а(). (9)
Смотрите также:
Решение задач по математическому анализу
| Геометрическая интерпретация | Решение Тейлора и Д. Бернулли |
| Задача о колебании струны | Спор по поводу задачи о колебании струны |

