Оглавление:






Регулярная прецессия симметричного твердого тела, имеющего неподвижную точку
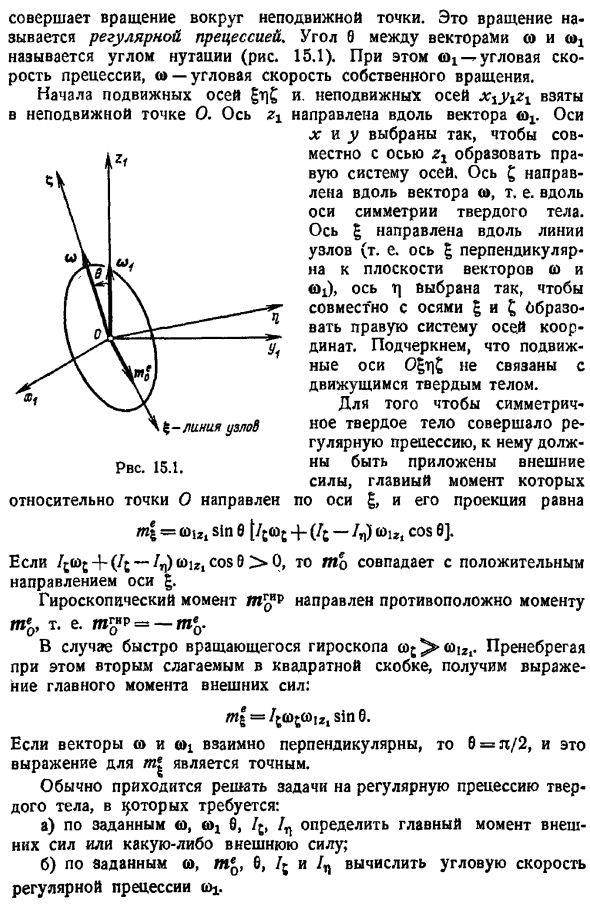
- Симметричное твердое тело вращается с постоянной угловой скоростью o вращается вокруг оси, затем с постоянной угловой скоростью a. Твердое тело, приводящее к комбинации вращений вокруг 2 пересекающихся осей. Вращайтесь вокруг неподвижной точки. Это вращение называется обычной прецессией. Угол между вектором и вектором wj называется углом движения рис. 15. 1. Кроме того, dj-угловая скорость прецессии, а co-угловая скорость вращения сама по себе. Начиная с движущейся оси неподвижная ось x1y1r1 получается в неподвижной точке o. Ось zi направлена вдоль вектора co. Ось ФЭС. 15. 1. Относительно точки o x и y выбраны для формирования правильной системы осей вместе с осью.
Ось направлена вдоль вектора o, то есть вдоль оси симметрии твердого тела. Ось z направлена вдоль линии узла то есть ось z перпендикулярна плоскостям векторов co и coj, а ось z выбрана для формирования правильной системы координат оси вместе с осью z и осью z. Подвижная ось o z не связана с движущимся телом. Для того чтобы симметричное твердое тело совершало регулярную прецессию, прикладывается внешняя сила, главный момент которой находится вдоль оси по, а проекция — 4 и грех в jcoj zj-zn 0iz1 cos. Если zc oj — z tou, cos 9 0, то m o совпадает с положительным направлением оси. Противоположное направление момента mn, т. е.
Начало отсчета оси х по-прежнему расположим в положении статического равновесия груза и ось х направим по вертикали вниз. Людмила Фирмаль
В случае с гироскопом co — социальный, который быстро вращается. Если мы проигнорируем 2-й член в скобках, то получим выражение главного момента внешней силы. СЛН 0- Если вектор co и coi перпендикулярны друг другу, то 6 l 2, и эта формула для m точна. Обычно приходится решать задачи, связанные с обычной прецессией твердого тела. А определить главные моменты внешних или внешних сил относительно заданного co, coj 6, zj, zn. B учитывая, m, 6, и zn, вычислите угловую скорость регулярной прецессии oj. Для решения задачи обычной прецессии твердого тела рекомендуется в следующем порядке 1 Выберите неподвижные оси xy r и подвижные оси, которые не связаны с твердым телом.
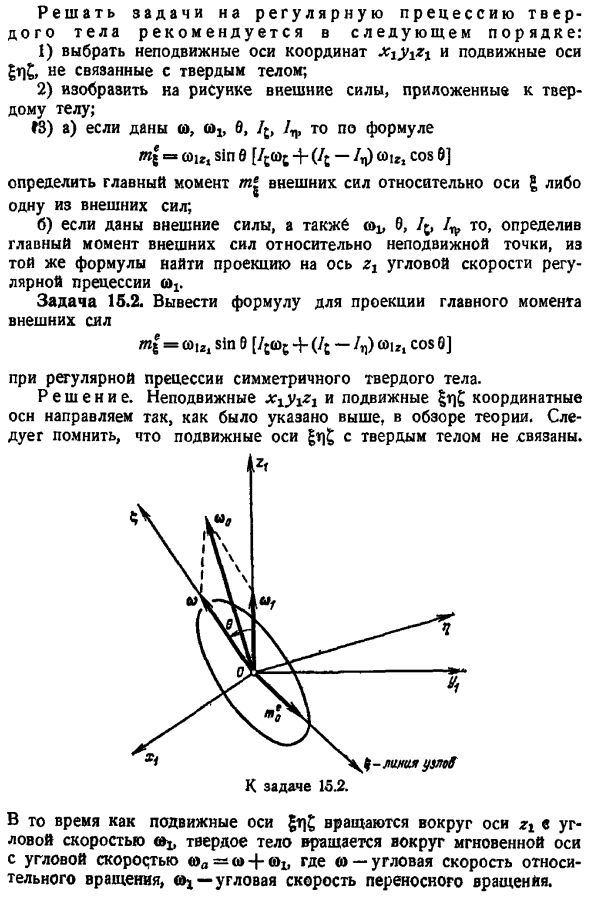
Внешняя сила, приложенная к твердому телу, показана на рисунке. Mz a u, i, , , zj, если задано 1, то выражение И грех в zt-i j a u, cos 6 Определяется главный момент 1 внешней силы или внешняя сила для оси Т j. б дана внешняя сила, кроме того, можно найти проекцию на ось угловой скорости прецессии, исходя из той же формулы, если определить главный момент внешней силы относительно неподвижных точек, zin, z. Задача 16. 2. Выведите формулу предсказания главного момента внешней силы М Ж 2, то sin 9 от zj 0 от zj-или z4 я и21 Косинус 0 Симметричное твердое тело с регулярной прецессией. Решение.
Зафиксируйте фиксированную систему координат x — y и переместите m, как показано в исследовании теории выше. Далее обратите внимание, что движущаяся ось gr не связана с твердым телом. Движущаяся ось m 5 вращается вокруг оси e с угловой скоростьюx. Твердое тело вращается вокруг мгновенной оси с угловой скоростью0 oi. Где 0-угловая скорость относительного вращения, а j-угловая скорость переносного вращения. , d, при расчете проекции u0 и w1 на ось следует отметить, что параллелограмм угловой скорости находится в плоскости. Л л 0, oln о л, синус, tojj С0 Г1mos 0. ЖЖ.
С помощью этих формул вы можете 0c 0 П 0 0op Шл 0 1П o z, sin 9, coac ШС — ШС 1 1cos 9- В результате главные моменты симметричного импульса твердого тела относительно оси g, z, являющейся главной осью инерции в неподвижной точке o, имеют следующий вид lj j 0a 0, dl zn 0at tit0 21sin9, z. J-zjciinjs Т c0j а із, cos9. 2 Потому что l, ln и являются константами, dlt.
Для определения главного момента внешней силы относительно точки o используйте динамическое уравнение Эйлера дю — ДТ ш-т — мл р-он 1сЦ — Н — ДжейТи ДЖП с — a1pc Подставляя значения, 1, из уравнения 1, lj, lv d из уравнения 2 и dl dt, dl dt, dl dt, dl dt, dl в уравнение 3, уравнения Эйлера принимают следующий вид 71j 0 2 грех 9 установки zj 0 г от zj- л КТ 2, потому что 0 тял 0, М 0. Таким образом, основной момент внешней силы m0 относительно неподвижной точки o лежит на линии узла и совпадает с положительным направлением оси. ФЛ —, соц, потому что 9 0. Задание 15. 3.
Вычислите угловую скорость обычной прецессии симметричного твердого тела, где центр тяжести находится в неподвижной точке. Если 9-угол между осью симметрии и прецессией, то это означает инерцию твердого тела относительно оси Метрика, j n, — это момент инерции на экваторе твердого тела и угловая скорость вращения в нем самом вокруг оси симметрии. Решение. Подвижный t и фиксированный старт оси xiyfa Находится в фиксированной точке вдоль оси прецессии, а ось и ji таковы, что вместе с осью zt они образуют правильную систему координатных осей.
- Подвижная ось ориентирована вдоль оси симметрии твердого тела, а ось. Вдоль линии узла ось m выбрана для формирования правильной системы координатных осей наряду с осями g и. На твердое тело действуют 2 силы гравитация и опорная реакция, центр тяжести совмещен с неподвижной точкой О, так что к точке О приложены обе внешние силы и ее главный момент Поскольку точка 0 равна нулю, она равна 0. Поэтому выражение для определения А. Неподвижной оси zj-это направлено на ЗР. К заданию 15. 3.
Проекция главной точки. СШ Ши, Косинус 0 cshe Т-Эй, Ши, потому что 0 Принимать форму Ши, cos 0 zt — lj w u, cos 0 0 Где искомая угловая скорость нормальной прецессии Рассматриваемая регулярная прецессия возникает при инерционном движении. Заметим, что обычная инерционная прецессия возможна вокруг оси, проходящей через неподвижную точку. Задача 15. 4. Определить угловую скорость регулярной прецессии 1 1 симметричного твердого тела массой p, возникающей под действием силы тяжести. Расстояние от центра тяжести твердого тела с неподвижной точкой o является.
Первые два слагаемых в правой части дифференциального уравнения (2), на основании формулы (3), уничтожаются. Людмила Фирмаль
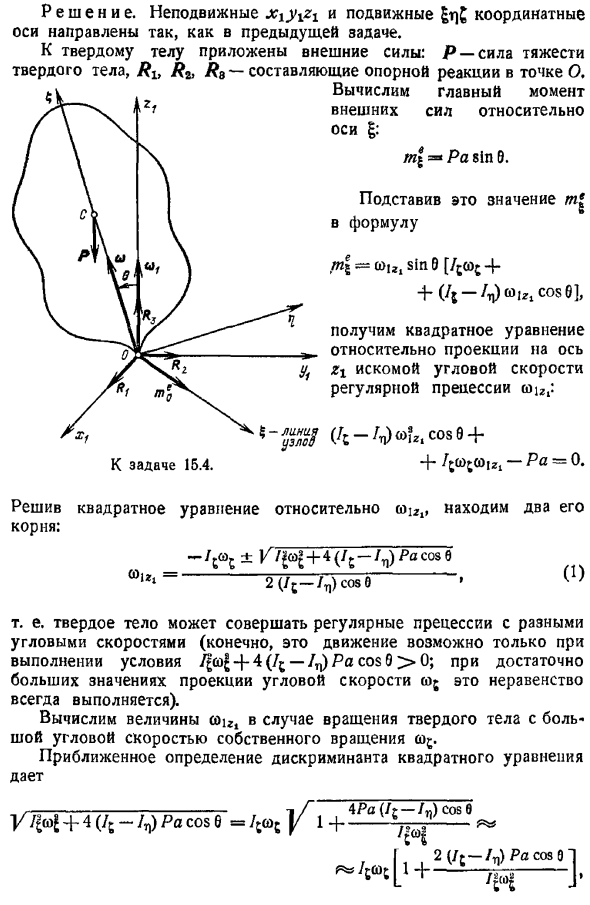
Даны момент инерции твердого тела относительно главной оси инерции, скорость вращения w вокруг оси симметрии и угол 6 между осью симметрии и прецессией. Решение. Фиксированные оси xiy и перемещения обозначены, как и в предыдущей задаче. К твердому телу приложена внешняя сила p-сила тяжести К заданию 15. 4. Поддерживает реакцию в точке o. Вычислите главные моменты внешних сил относительно оси g. i Ра Син Б.
Присвойте это значение выражению от От coi, , sinb tcot j-a wlz, cosb Получим уравнение 2-го порядка для проекции искомой угловой скорости a1zl нормальной прецессии на ось yt zi. С-ИИ з ко 0 0 р — ра 0. Если вы решите квадратное уравнение относительно, вы найдете его 2 корня. Л ———- То есть твердое тело может совершать регулярную прецессию при различных угловых скоростях конечно, это движение возможно только при условии 7 ci j 4 t — n pa cos b 0. Если величина проекции угловой скорости wj достаточно велика, то это неравенство всегда будет выполняться. Для вращения твердого тела 0j, собственная скорость вращения которого велика, вычислите величину a u.
Приближенное определение дискриминанта квадратичного уравнения является РВ лфт-ВФ — т я к −7 — — Ч1 — j. 2 С — Л Вт Пакос Введите значение 1 в Формулу 2 и вы найдете нужную приблизительную проекцию угловой скорости обычной прецессии. Угловая скорость медленной прецессии И угловая скорость прецессии Величина проекции угловой скорости быстрой прецессии совпадает со значением проекции угловой скорости обычной прецессии вследствие инерции, полученной в предыдущей задаче. Величина проекции угловой скорости медленной прецессии совпадает с результатами, рассчитанными при решении аналогичной задачи с использованием приближенной теории гироскопов см. 2, стр. 563. Задача 15.
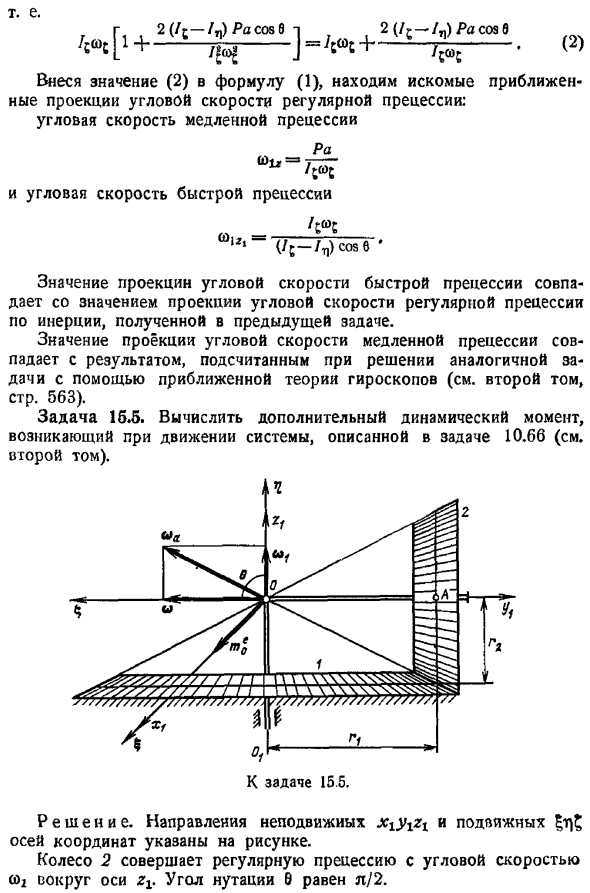
Вычислите дополнительные динамические моменты, возникающие при движении системы, описанные в выпуске 10. 66 см. 2-й том. Решение. Направление неподвижных x zi и подвижных осей показано на рисунке. Колесо 2 совершает регулярную прецессию с угловой скоростью a r вокруг оси zi, а угол подкачки 0 равен l 2. Вычислить главные моменты внешних сил по формуле Я СЛНУЦС4- — А икос 1-О Если 6 — g -, то m соответствует результату Получаем в уравнении выпуска 10. 66 3 см.
Том 2, 1-tl Используя формулу 1, Вы получаете результаты быстрее, чем применяя теорему Резаля. Это решило задачу 10. 66, но мне нужна информация о динамике твердого тела, вращающегося вокруг неподвижной точки. Формула 1 также может быть применена для решения задачи в Томе 2 10. 64 и 10. 65. Задача 15. 6. Решите задачу 10. 16 см. 2 использование теории обычной прецессии симметричных твердых тел. Решение. Решение Тома 2, выпуск 10. 16, основанное на кинетическом методе, было довольно трудоемким.
Она была сведена к системе из 4 уравнений На НБ типа МХС л musv n a y 4-МВА — МхсУ Синяя Н-Н byb −1ug 1hue, -н а в НБ б Иксия полный 1ug. Кроме того, центробежный момент инерции и первый расчет 1y был определен раньше, поэтому потребовалось много вычислений, чтобы решить задачу 2-го тома 9. 12. Эта задача может быть решена значительно короче, если рассматривать вращение цилиндра вокруг оси z как частный случай регулярной прецессии при отсутствии собственного вращения вокруг оси z. Для этого достаточно определить гироскопический момент цилиндра дазира.
Это момент силы инерции и уменьшается до пары боковых дополнительных динамических давлений, необходимых для опор а и в psir — te0 Поскольку ось 9 этой задачи обозначается через a Дагир — о 11 джин на 4 — г-дя 1ccos а. 1 Из-за отсутствия правильного вращения 05 0 угол поворота цилиндра вокруг оси zj равен угловой скорости обычной прецессии, поэтому a необходимо заменить на. Где выражение 1 принимает вид Л р р т-у грех потому что. Момент гироскопа — это момент, когда опоры a и b на плече ab 2h подвергаются дополнительному боковому воздействию pressure. So.
Смотрите также:
Предмет теоретическая механика

