Оглавление:
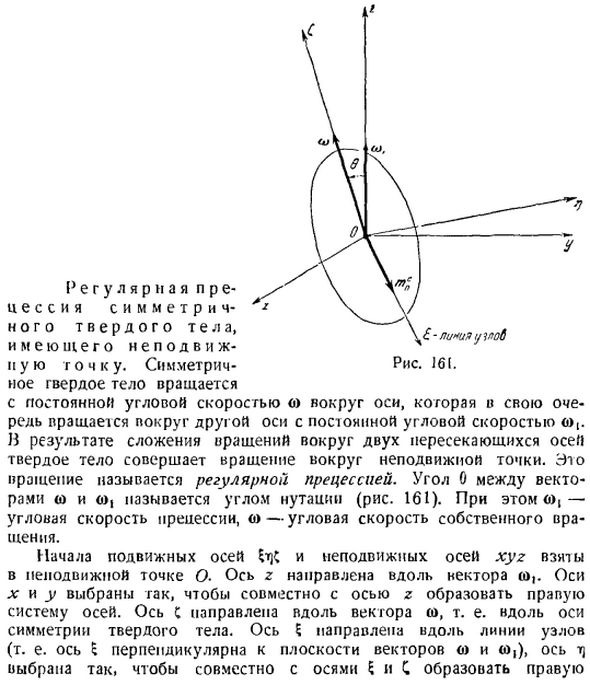






Регулярная прецессия симметричного твердого тела, имеющего неподвижную точку
- Симметричное твердое тело вращается вокруг оси с постоянной угловой скоростью i, а ось вращается вокруг другой оси с постоянной угловой скоростью. Итог. С добавлением вращения вокруг 2 пересекающихся осей, твердое тело вращается вокруг неподвижной точки. Это вращение называется обычной прецессией. Угол между вектором o и 0 0 Он называется углом хода рис. 161. Кроме того, o1-угловая скорость прецессии, а o-угловая скорость вращения в себе. Начальная точка подвижной и неподвижной оси обруча берется неподвижной точкой o. Ось z ориентирована вдоль вектора. Оси x и y выбраны для формирования правой оси системы вместе с осью z.
Ось с направлена вдоль вектора w, то есть вдоль сплошной оси симметрии. Ось 5 ориентирована вдоль линий узлов то есть ось b перпендикулярна плоскости вектора и o. Выбрана ось m. Вместе с осями 5 и с образуют правильную систему осей. Подчеркните, что движущаяся ось не связана с движущимся телом. Для того чтобы симметричное твердое тело совершало регулярную прецессию, к нему необходимо приложить внешние силы, главный момент которых находится на оси относительно точки О.
Используя теорию нормальной прецессии симметричного твердого тела, решите задачу 375. Людмила Фирмаль
И алгебраические величины равны М 51n 0 С с-б — с-,. W1l потому что б у. Если c c4- c-a и cos 6 0, то t o соответствует положительному направлению оси c. Момент m p гироскопа направлен в противоположную сторону от моментаo. То есть, m3 p — Для быстро вращающегося гироскопа, a 0 2. Если мы проигнорируем пункт 2 в скобках, то получим выражение главного момента внешней силы, уже найденное из приближенной теории гироскопов.
Если векторы w и o1 перпендикулярны друг другу, то 0 -и это выражение m является точным. Обычно приходится решать задачи, связанные с обычной прецессией твердого тела. А определить основные моменты внешних или внешних сил в соответствии с заданными о, Шц о, С. B для заданного co, m o, 0, fc вычисляет угловую скорость w регулярной прецессии. Рекомендуется решать задачу обычной твердотельной прецессии в следующем порядке. 1 Выберите неподвижную ось объятия и подвижную ось ns, связанную с твердым телом. 2 внешняя сила, приложенная к твердому телу, показана на рисунке. 3 a если указаны o, n0, c, то выражение 5 Кайминьш 0 СШС 4 — С — П Косинус 0 Определите точку t 1.
Одна из внешних или внешних сил к оси. B 0 6 п, а также определить главный момент внешней силы относительно неподвижной точки, когда внешняя сила задана, и из этой же формулы найти проекцию угловой скорости обычной прецессии на ось z оР Задача 424. Выведите выражение, представляющее алгебраическое значение главного момента внешней силы m — Я199 9 ss, — — — w, cos0 Прецессия симметричного твердого тела. Зафиксируйте обнимать и подвижные координаты как выше Плоскость т к Скорость есть В обычном Ре 1пе н и Е. Оси, на которые мы указываем, были обозначены обзором теории. Должен Обратите внимание, что движущаяся ось t c не связана с твердым телом.
В то время как движущаяся ось cs вращается вокруг оси z с угловой скоростью 0, твердое тело вращается вокруг мгновенной оси с угловой скоростью 1 d o. Где o-угловая скорость относительного решения, , — угловая скорость переносного вращения. При расчете проекций oa и co, c на оси m и c, необходимо иметь в виду Параллелограмм угла можно увидеть на рисунке 0. 5 0, w 0 и 5 pv, 0k 0, 2 cos 0. С помощью этих формул вы можете 0-4 0. 5 0 0Л 4 — 1 п П1 р ж 0 h 0 4-w1g so8 b- Таким образом, главные моменты импульса симметричного твердого тела относительно оси m, c, являющейся главной осью инерции в неподвижной точке o, имеют вид 0 4 s os 4 — oi с 0.
Потому что d и ds-константы Л- 41 л 11 Г я 3 Используйте динамические уравнения Эйлера для определения главных моментов внешней силы относительно точки О. После замены значения, w1c из уравнения i, уравнение—1. 3 из уравнения 2 и-уравнение 3 Мнение Эйлера имеет следующую форму 81 П 6 с ОС с-Потому что 6 Теги, О 0. В результате основной момент внешней силы относительно неподвижной точки о ТЭП оказывается на линии. —— — -. ..
Если он соответствует положительному направлению узла и оси — l и co5 6 0. Задача 425. Вычислите угловую скорость обычной прецессии симметричного твердого тела, где центр тяжести находится в неподвижной точке. Если 9-угол между осью симметрии и прецессией, то 1g-момент инерции твердого тела относительно оси симметрии, а 4 n-экваториальный момент инерции твердого тела. Тело — это угловая скорость его собственного вращения вокруг оси y симметрии. Решение. Начальная точка объятия подвижной и неподвижной осей находится в неподвижной точке o.
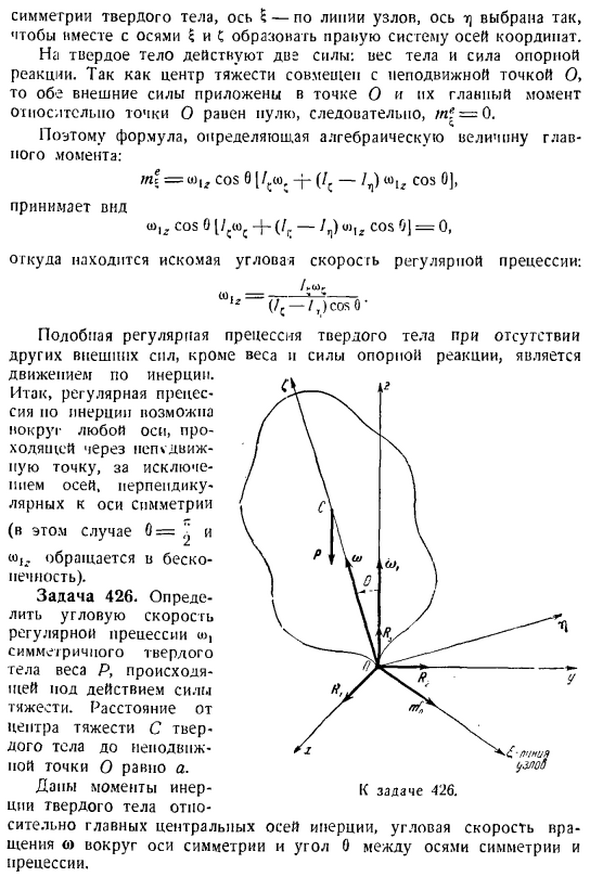
Неподвижная ось 2 ориентирована вдоль оси прецессии, а оси x и y ориентированы вместе с осью x, чтобы сформировать правильную систему координат для axis. Is подвижная ось c ориентирована вдоль оси симметрии твердого тела, а ось c расположена вдоль линии узлов, а ось m выбрана так, чтобы иметь ось И c образуют правую систему осей. Сила dvg действует на твердое тело вес тела и сила реакции поддержки. Центр тяжести совмещен с неподвижной точкой о, так что к точке О приложены обе внешние силы, А главный момент для точки о равен пуле, поэтому l 0. Итак, формула, определяющая алгебраические значения основных моментов, выглядит следующим образом Яс 0, Соз о. Он принимает вид, p s — p 01g pop 0 Вт.
- Потому что 0 ССК-ч 1г — г м 1х потому что 0 0 Откуда берется искомая угловая скорость нормальной прецессии. Аналогичная нормальная твердотельная прецессия при отсутствии Внешняя сила, отличная от веса и прочности По инерционному движению. Именно поэтому регулярная прецессия возможна вокруг любой оси, проходящей через неподвижную точку, за исключением оси, перпендикулярной оси симметрии в этом случае 0 и с-бесконечно. Задача 426.
Определить угловую скорость 1 регулярной прецессии симметричного твердого геля массой p, возникающей под действием силы тяжести. Расстояние от центра тяжести твердого тела с неподвижной точкой o является. Данный момент Ответ поддержки Твердотельный Скорость вращения вращения вокруг оси симметрии, угол 0 между осью симметрии и осью разности, относительно основного инерционного центра axis. Solution. As в предыдущей задаче показано перемещение неподвижных осей КС. Внешняя сила приложена к твердому телу p-масса твердого тела, p, i 2, Р3-составляющая опорной реактивной силы в точке О.
Вычисляет главные моменты внешней силы относительно оси Пи. Людмила Фирмаль
Присвойте это значение выражению С А — — С — П 81n. Получаем уравнение 2-го порядка для проекции искомой угловой скорости нормальной прецессии на ось z o1r С- Р 0 п cos0 о — па 0. Если вы решите квадратное уравнение относительно, вы найдете 2 его тела. — 0. 2 1 4-4 — g raco50 1g 2- g Соз 0 То есть твердое тело может совершать регулярную прецессию с различными угловыми скоростями конечно, это движение возможно только при выполнении условия-4 c —, 0 0 для достаточно больших проекций угловых скоростей неравенство всегда верно.
Вычислите величину. Если угловая скорость собственного вращения велика, то вращение твердого тела Приближенное определение дискриминанта квадратичного уравнения выглядит следующим образом 4 и С05 6 с ря 1 4rd gc — t1 s x0 1 С 2 С- Л rdso8 0, , 2 С — Г П 0 — Б-7 — — — — — — — Р р т——— ——— л ы с Вводя это значение в формулу i, мы видим искомое приближенное значение проекции угловой скорости обычной прецессии угловая скорость медленной прецессии РА Ш. — И угловая скорость прецессии С, Р С- Т кост Величина проекции угловой скорости быстрой прецессии совпадает со значением проекции угловой скорости обычной прецессии, но инерция была получена в предыдущем случае.
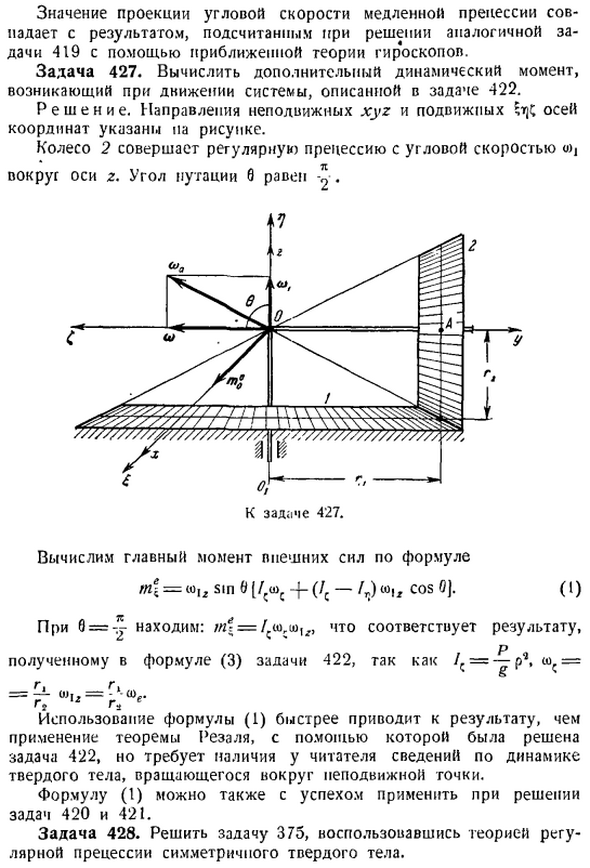
Величина проекции угловой скорости медленной прецессии 419 совпадает с результатами, рассчитанными при решении аналогичных задач с использованием приближенной теории гироскопов. Задача 427. Вычислите дополнительные динамические моменты, возникающие во время движения системы, описанного в задаче 422. Решение. Направление неподвижного обруча и движущихся осей координат показано на рисунке. Колесо 2 подвергается регулярной прецессии с угловой скоростью b1 вокруг оси d. Углы Главы 6 равны. Вычислить главные моменты внешних сил по формуле И- 0 2 51p 6 s —, Соз с. Если 8, то результат соответствует m. П — Итак, получаем в задаче 422 уравнение 3 г. — Кто —О -.
Используя формулу 1, Вы получаете результаты быстрее, чем применяя теорему Резаля, используемую для решения задачи 422, но вам нужна информация о динамике твердого тела, вращающегося вокруг неподвижной точки. Уравнение 1 также может быть успешно применено для решения задач 420 и 421. Задача 428. Solution решение.
Решение задачи 375, основанной на методе кинетической статики, было достаточно простым. Laborious. It была сведена к системе из 4 уравнений. М bx mxc по Муз е м АУ нет. Мну г — типа МХС е м aua-ЛД, б — 1г х е −4 1 Тсс Н yg8 карбида. В этом случае центробежные моменты инерции x и 1uh определяются заранее. Расчет 1xg требовал выполнения большого количества вычислений при решении задачи 314.
Эта задача может быть решена значительно короче, если рассматривать вращение цилиндра вокруг оси z при отсутствии вращения вокруг оси с как частный случай регулярной прецессии. Для этого достаточно определить гироскопический момент mn, p цилиндра. Это момент инерции, который уменьшается до дополнительных боковых динамических пар давления, необходимых для опор a и b mt1 p — te0. Потому что в главе 6 угол поворота этой задачи представлен a yagir w 2 81p a c ac 4 — c — l a 1r cos a. 1 Поскольку нет правильного вращения, a 0, w1r должен быть заменен на w. Это связано с тем, что угловая скорость вращения цилиндра вокруг оси 2 является угловой скоростью обычной прецессии.
Где выражение 1 принимает вид М111 Р Л- Г Вт ЗШ и соз. Рг2 П г — Для цилиндра у — Х е Р п 4 м м 81n 2а Момент гироскопа — это момент, когда опоры a и b на плече ab 2l подвергаются дополнительному боковому давлению. Следовательно, М Нет. 0 31П 2а.
Смотрите также:
Предмет теоретическая механика
| Приближенная теория гироскопа | Задачи динамики материальной точки |
| Динамика твердого тела, вращающегося вокруг неподвижной точки | Задачи динамики системы материальных точек |

