Регрессионные модели с количественными и качественными переменными
Модели, которые содержат количественные и качестенные факторные признаки, называются ANCOVA — моделями (моделями ковариационного анализа). Простейшая ANCOVA — модель с одним количественным и одним качественным признаками имеет вид:
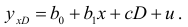
Ожидаемое значение результативного признака при альтернативных значениях фиктивного признака равно:
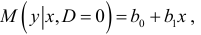
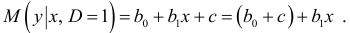
Из моделей (5.2) и (5.3) следует, что значение результативного признака изменяется с одним и тем же коэффициентом пропорциональности 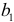 отличаются лишь свободные члены на величину
отличаются лишь свободные члены на величину 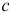 . Проверив при помощи
. Проверив при помощи 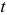 -статистики статистические значимости коэффициентов
-статистики статистические значимости коэффициентов 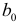 и
и 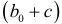 , можно определить влияние фиктивной переменной на результативный признак. При статистической значимости коэффициентов подтверждается влияние фиктивного фактора на результативный признак.
, можно определить влияние фиктивной переменной на результативный признак. При статистической значимости коэффициентов подтверждается влияние фиктивного фактора на результативный признак.
Значение фиктивного признака при 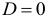 называется базовым или сравнительным. Коэффициент
называется базовым или сравнительным. Коэффициент 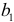 в модели (5.1) называется дифференциальным коэффициентом свободного члена, так как он показывает, на какую величину отличается свободный член модели при значении фиктивной переменной, равным единице, от свободного члена модели при базовом значении фиктивной переменной (при
в модели (5.1) называется дифференциальным коэффициентом свободного члена, так как он показывает, на какую величину отличается свободный член модели при значении фиктивной переменной, равным единице, от свободного члена модели при базовом значении фиктивной переменной (при 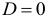 ).
).
В регрессионную модель можно вводить произвольное число качественных переменных. Например, регрессионная модель с двумя качественными признаками имеет вид:
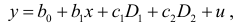
где

Из этой модели выводятся следующие регрессионные зависимости:
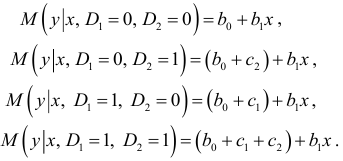
Регрессии отличаются лишь свободными членами. Дальнейшее определение статистической значимости коэффициентов 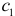 и
и 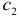 позволяет убедиться, влияют ли фиктивные факторы на результативный признак.
позволяет убедиться, влияют ли фиктивные факторы на результативный признак.
Описанные схемы могут быть распространены на регрессии с произвольным числом количественных и качественных факторов, при этом отметим, что если качественный фактор имеет 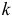 альтернативных состояний, то для его описания используется
альтернативных состояний, то для его описания используется 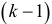 фиктивных переменных.
фиктивных переменных.
В рассмотренных выше случаях, предполагалось, что изменение значения качественного фактора влияет лишь на изменение свободного члена. Но существуют ситуации, когда изменение качественного фактора приводит к изменению, как свободного члена уравнения, так и коэффициента регрессии. Это характерно для временных рядов экономических данных при изменении институциональных условий, введении новых правовых или налоговых ограничений. В этом случае уравнение регрессии будет иметь вид:
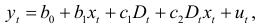
где
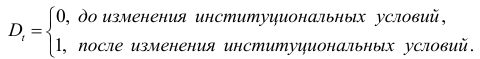
Ожидаемые значения результативного признака определяются уравнениями:
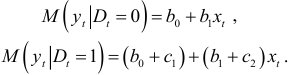
Коэффициенты 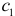 и
и 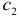 в уравнении (5.5) называются дифференциальным свободным членом и дифференциальным угловым коэффициентом соответственно. Фиктивный фактор
в уравнении (5.5) называются дифференциальным свободным членом и дифференциальным угловым коэффициентом соответственно. Фиктивный фактор 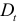 в уравнении регрессии (5.5) используется как в аддитивном виде
в уравнении регрессии (5.5) используется как в аддитивном виде 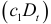 , так и в мультипликативном
, так и в мультипликативном 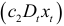 , что позволяет разбивать уравнение регрессии на два уравнения, связанные с периодами изменения рассматриваемого в модели качественного фактора.
, что позволяет разбивать уравнение регрессии на два уравнения, связанные с периодами изменения рассматриваемого в модели качественного фактора.
Для ответа на вопрос, можно ли за весь рассматриваемый период времени строить единое уравнение регрессии, или же нужно разбить временной интервал на части и на каждой из них строить свое уравнение регрессии, используется тест Чоу. Применение теста Чоу состоит в следующем.
- Строится уравнение регрессии по выборке объема
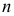 и вычисляется сумма квадратов отклонений значений
и вычисляется сумма квадратов отклонений значений 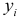 от общего уравнения регрессии:
от общего уравнения регрессии: 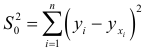 .
. - Выборку разбиваем на две подвыборки объемами
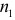 и
и 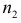 соответственно
соответственно 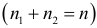 .
. - Для каждой из подвыборок строим уравнения регрессий и вычисляем суммы квадратов отклонений
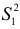 и
и 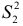 значений
значений 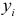 для каждой из подвыборок, от соответствующих уравнений регрессий.
для каждой из подвыборок, от соответствующих уравнений регрессий. - Проводим сравнение дисперсий на основе
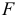 -статистики:
-статистики:
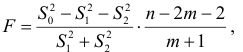
имеющей распределение Фишера с числом степеней свободы 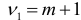 и
и 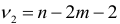 , где
, где 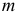 -число факторных признаков во всех трех уравнениях регрессий.
-число факторных признаков во всех трех уравнениях регрессий. 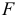 -статистика близка к нулю, если
-статистика близка к нулю, если 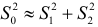 . Тогда
. Тогда 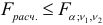 и это означает, что нет смысла разбивать уравнение регрессии на части. Если же
и это означает, что нет смысла разбивать уравнение регрессии на части. Если же 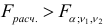 , то это означает необходимость введения в уравнение регрессии фиктивной переменной, т.е. целесообразность разбиения на подвыборки с точки зрения улучшения качества модели.
, то это означает необходимость введения в уравнение регрессии фиктивной переменной, т.е. целесообразность разбиения на подвыборки с точки зрения улучшения качества модели.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
| Мультиколлинеарность экзогенных переменных |
| Модели с дихотомическими (фиктивными) переменными |
| Модели с фиктивными результативными признаками |
| Системы уравнений используемых в эконометрике |

