Рефракция

Рефракция

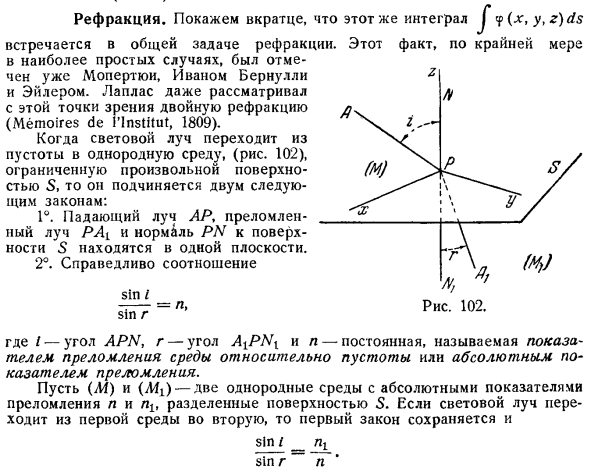
• Легко видеть, что один и тот же Интеграл J 4 x, y, z ds встречается в общих задачах преломления. Этот факт, по крайней мере в самом простом случае, был замечанием. Уже МО Пертви, Иван Бернулли, Эйлер. Лаплас также рассматривал двойную рефракцию с этой точки зрения Memoires de l Institute, 1809. Когда луч света достигает однородной среды рис. 

Окруженной произвольной поверхностью S из пустоты, он следует следующим 2 законам: 1.Падающий пучок AP, преломленный пучок PAl и нормаль поверхности s PN находятся в одной плоскости. 2.Справедливое соотношение Я виноват. Син р н Рисунок 102. Где угол APN, r угол, а n постоянная величина. Преломляющее тело среды по отношению к пустотам или абсолютным показателям преломления. A4 и Afi как 2 однородные среды с абсолютным показателем преломления n и ni, разделенные поверхностью S Грех призраки НТ sin g 7G вспомните эти законы и приступайте к следующей задаче. Пусть А и А Есть 2 точки На одной или другой стороне S, где P любая точка на этой поверхности.

В самом деле, отнесем плоскую кривую к оси вращения, принятой за ось Ох, и перпендикулярно к последней направим ось Оу. Людмила Фирмаль

Каким должно быть положение точки P Пенсильвания Это был минимум 2 прямые AP и PA указывают на то, что минимальное значение получается, когда закон преломления соблюдается при переходе от среды M к среде Aft. фактически, в a, b, c координаты точки A, когда представлены alf blf q координаты точки Ar, а x, y, z координаты точки P, расстояние AP и a P будут иметь значения соответственно Ф Х с 2 не 2 НД с 3 и V х В1 1 + г БТФ + Р С1А поскольку z является функцией x и y, которая определяется 0 в формуле f x, y, z = S, сумма o является функцией 2 независимых переменных x и y. to найдите значение xnu, которое переворачивает a до минимума, используйте частную производную a относительно x и y. 

• Мы получим 2 уравнения. х а + у с г Н ха 4 х + у ТТ = =Да. г Б + Z с Н = y 4 РА РА. Определите координаты точки P вместе с уравнением поверхности. После определения этой точки замените оси. Точка P в качестве начальной точки рис. 102, нормальная ось к точке A это ось Oz, а плоскость, содержащая A, плоскость zz. значение x, точка P будут равны нулю, и полученное уравнение ДЗ ДЗ г ДХ ду будет т0. Наха О, = 0.

Выражение указывает, что точка а также находится в плоскости zpx, которая представляет собой первый закон преломления. Первое уравнение показывает, что ax отрицателен, и если угол, образованный отрезками AP и PAi in u, выражается как Нормаль Pz, то из этого уравнения мы получаем следующее уравнение: Н грех я 1 грех г = 0 так как a PA и a PAi равны греху I и греху g, то это 2 й закон refraction. So, вдоль пути, по которому лучи идут от А к ЛП, получается необходимый минимум. Представьте, что некоторые поверхности разделяются Однородная среда. Абсолютный показатель преломления n помещается над средой показателя преломления между Sx и 52 до S, показателем преломления n и, наконец, под Sp.

Площадь поверхности, образованной вращением плоской кривой вокруг оса, расположенной в ее плоскости и ее не пересекающей, равна длине этой кривой, умноженной на длину окружности, описываемой ее центром тяжести, в предположении, что кривая однородна. Людмила Фирмаль

Возьмем точку B первой средней точки A, точку B последней средней полигон AP P2… рассмотрим ППБ. Каждая поверхность из точки A в точку B имеет вершину рис. 103.Если вы хотите узнать, каким должен быть этот полигон для суммы а = нагр 4 н р е + prPrV Это был минимум, но по предыдущему примеру, согласно закону преломления, видно, что Луч это путь, идущий от А до В. Наконец, число поверхностей увеличивается бесконечно, и далее разница между сторонами многоугольника n n n n2,… Предположим, у вас есть тенденция к нулю. А потом сова.

Целостность рассматриваемой среды абсолютный показатель преломления n становится непрерывной средой, которая является непрерывной функцией координат Y x, y, z .Многоугольник трассировки лучей становится кривой, а сумма a становится интегралом. Рисунок 103. В Один Таким образом, путь лучей Из точки A в точку B мы составляем дифференциальное уравнение, которое соответствует кривой, минимизирующей Интеграл. O для этого вопроса. Вы можете обратиться к статье Бонэ Nouvelles Annales de Mathfematiques, 1887.Та же кривая была исследована Викером Comptes Rendus, vol. CVII1, p. 

Смотрите также:

Решение задач по теоретической механике

Исследование одного определенного интеграла. Геометрическая задача	Натяжение и изгибающий момент
Формула Тэта и Томсона	Ось стержня была первоначально дугой окружности