Оглавление:











Ребристая поверхность нагрева
- В первой главе было показано, что общее тепловое сопротивление вашей 1 плоской стенки определяется максимальное тепловое сопротивление в частном секторе. Если последний является конвективным резистором, то тепловой поток через стенку максимален на месте\ Сопротивление. Поверхности нагрева с ребрами, например, экономайзер паровых котлов, радиатор систем парового и водяного отопления Электрические трансформаторы, двигатели внутреннего сгорания с воздушным охлаждением цилиндров, авиационные двигатели и др.
Прямоугольные ребра. Самым простым случаем является расчет квартиры Поверхность с ребрами. Если Высота ребра трубы относительно невелика, то можно применить полученную формулу плоскостности для расчета цилиндрической ребристой поверхности Поверхность с ребрами. Для ребра определенной толщины высоты I справедлива формула, полученная в§ 3-4.Используйте нотацию иллюстрации. 3-7, площадь поперечного сечения ребра равен bL, периметр C = 2L. это верно, если b мало для L. значение m определяется путем подстановки значений, которые находятся в Формуле «ребро теплопотерь».
Стоимость, масса и габариты теплообменника. Людмила Фирмаль
Из формул(3-23) и(3-26). очень важно знать условия, при которых ребристая поверхность является более выгодной, чем плоская поверхность. Ответ на этот вопрос зависит от относительной важности факторов. Прежде всего, необходимо ответить на вопрос, в каких условиях ребра увеличивают тепловой поток через стенки. Ребра, очевидно, являются выгодными, когда тепловой поток через ребро увеличивается по мере увеличения высоты ребра. Если тепловой поток уменьшается с увеличением высоты ребер выгоднее сделать реберные кости как можно ниже.
То есть выгоднее вообще не полагаться на ласты all. So, предельные условия прибыльности Финна описаны в уравнении NN(3-28). Используя формулу(3-26), можно получить травление results. In рассматриваемую задачу X, A, m и O можно считать постоянной величиной, поэтому формула(3-26) Достаточно различить только числитель и знаменатель дроби. Если числитель равен нулю или знаменатель бесконечно велик, результирующее выражение равно нулю. Значение. — Последнее соответствует тривиальному решению X = 0, так как это значение удовлетворяет решению формулы (3-28).Поэтому мы рассматриваем только молекулы. Дифференцирование Для числителя формулы(3-26) получены следующие результаты: после упрощения вы получите выражение присваивания формулы (3-27).(3-29)левая часть последнего уравнения имеет вид.
Сопротивление жары передачи тепла, и «правильной стороны», сопротивление жары плоской теплопроводности стены 2 раз толщины нервюры. Как тепло Сопротивление такое же по размеру, плавники бесполезны. Конечно, фактическое условие, которое является свойством короткого края[формула (3-26)]、 Он отличается от того, что принято в расчете. тепловой поток и изотермы таких краев бета-реальности имеют вид, показанный на рисунке 2. З-В, и » выше В расчетах температура изменяется только в направлении высоты, поэтому предполагалось, что она постоянна в плоскости, перпендикулярной оси ребра.
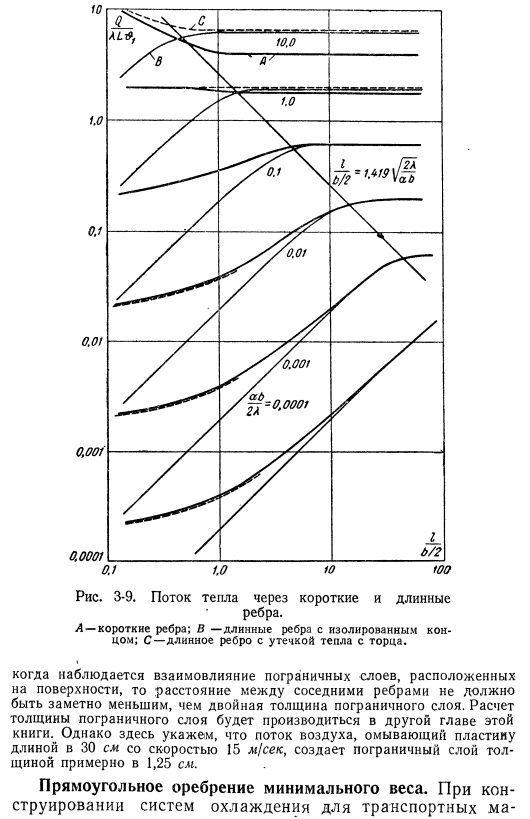
Эта ситуация отражена в Числовое выражение формулы(3-29).Однако верно, что в условиях-> 5 выгодно опираться на поверхностные ребра. (3-30) рисунок 3-9 сравнение Тепловой поток через основание 3 различных нервюр: a короткое нервюра, B длиннее нервюра с изолированными концами, C длиннее нервюра с утечкой жары от ends.
To На этом рисунке показана длина ребер. Это относится и к более простому анализу 1-го теплового потока, поскольку его можно считать длинным ребром. Пример 3-2 Необходимо определить, когда выгодно разместить чугунное ребро толщиной 3 мм на поверхности нагрева. Теплопроводность чугуна описана в приложении. Возьмите в среднем от 1 до 49 если ккал / м•ч * городского тепла передается воздуху, то значение коэффициента теплопередачи находится в диапазоне от 104 до 100 ккал {м * * ч-град.
Получить максимальное значение, 2>⁴⁹abab 100-0. 003 поэтому нагрейте воздух (или другой газ), ребра (поверхность полезна. Если тепло передается воде, то значение коэффициента теплопередачи составляет 5004-5000 ккал [м? •H * Shi если вы снова возьмете самое высокое значение,₌_ _ 2.49 g » d 5 000003 это значение очень низкое, поэтому ребра поверхности на самом деле Он не усиливает передачу тепла.
Эффективность ребер для жидкостей может быть повышена за счет использования металла с высокой теплопроводностью и тонкого ребра. Однако на практике толщина ребер составляет Сделать его значительно меньше 3 килограммов невозможно, так как теплопроводность самой теплопроводной меди всего в 5 раз выше теплопроводности чугуна. Передача тепла к жидкости increases. In в случае жизнеспособности изготовления ребер теплопередача увеличивается, если ребра расположены на максимально близком расстоянии друг от друга. Когда коэффициент теплопередачи уменьшается, рис. 3-8.Короткое ребро теплового потока с прямоугольным сечением.
Ребра. Л-ребрышки. Б-длинные реберные кости с изолированными концами. С-длинные ребра с утечкой тепла с торцов. Если наблюдается взаимное влияние пограничных слоев, расположенных на поверхности, то расстояние между соседними кромками не должно быть заметным Менее чем в 2 раза превышает толщину пограничного слоя. Расчет толщины пограничного слоя будет рассмотрен в другой главе этой книги. Однако, здесь, чистка воздушных потоков Пластины со скоростью 15 м/с и длиной 30 см создают пограничный слой толщиной около 1,25 см. Прямоугольные ребра с минимальным весом.
При проектировании системы охлаждения Особенно важно решить задачу максимального теплообмена при минимальном весе теплообменника для транспортных средств, особенно для самолетов. Устранение этой проблемы Ребристая поверхность. 1 вес ребра (рис. 3-7) T = P£6 / = p£Ln (3-31), где p-плотность материала ребра. Площадь поперечного сечения ребра, перпендикулярного Dx-L. Длина L задается, а значения b и I должны быть выбраны таким образом, чтобы тепловой поток через ребра был максимальным при заданных значениях D. подставим значение m =] /в уравнение(3-23 2a / 1b и a = bL (обратите внимание на разницу между A и Aₜ.D-сечение, перпендикулярное тепловому потоку, а Xi-сечение в плоскости рисунка (рис. 3-7).
Высота ребра I равна Сечение Д(/ =Д₁/ 6), получаем следующее: (3-32) формула(3-32) максимальное значение при dQi / d6 = 0; при дифференцировании уравнения (3-32)и наличии производной, равной нулю: 2 ^ b \ T XM / r V A x2 СН2 [/2а / объявление (ГДж / б)] замена(3-33) (3-34) дает Тха= -^ -. CH2 и его Трансцендентальные уравнения должны решаться численно или графически. Например, создайте график изменений в обеих частях уравнения и вместе с изменениями определите точки (пересечения Кривая. Таким образом, «получить значение» = 1,419 возможно. Таким образом, если верно следующее уравнение, то получается максимальный тепловой поток через край заданной массы. 1 4191 / -d / 2 ab. (3-35), как вы можете видеть из этого!
Отношение высоты ребер к толщине днища определяется теми же признаками, что и в уравнении (3-29). комплекс com b / o a ^ — / l был назван стандартом Biot, поскольку он часто встречается в задачах теплопроводности в условиях граничного конвективного теплообмена. Он… При изучении конвективного теплообмена он безразмерен и аналогичен числу нуссельта, которое мы встречаем. Однако между ними существует большая разница. Био-стандартная теплопроводность Теплопроводность, которая обусловлена проводником и, с другой стороны, выражается в числе нуссельта, относится к конвекции жидкости или газа. Чрезмерная температура на краю ребра.
Что касается температуры окружающей среды, то она равна: a«= ^ ’ = ° — ⁴⁵⁷ & — (3-36)это уравнение позволяет выяснить, достигается ли оптимальная высота ребер при заданном Oi. Если на поверхности нагрева нет ребра, то поверхность, равная площади поперечного сечения основания ребра, будет излучать тепло Q ’= abL ^ I. следовательно, отношение количества тепла — учитывая ребра, для количества тепла Q, для лучшего края по уравнению (3-32), следующие значения будут: J = KSth «= ° » ⁸⁸⁹ / F (33⁷ > this Уравнение определяет, насколько теплопередача может быть увеличена за счет оребрения поверхности нагрева. Например, чугунные ребра толщиной от 3 до 3 мм, значение 2X / a & равно 330.
Если подставить это значение в Формулу(от 3 до 35), то при теплопередаче на воздух вы получите оптимальное значение соотношения//(b / 2)= 25,8, при теплопередаче на воду//(b / 2)= 3,04.Для алюминиевых ребер Теплопроводность 178 ккал.1,0 толщина} m * h * ha * оптимальное соотношение 1 /(b / 2) составляет 85,1 по воздуху и 12,0 по воде. Толщина ребер Когда отношение теплового сопротивления теплопередачи к тепловому сопротивлению теплопроводности становится меньше, оно должно быть больше. Чугунные ребра будут очень слабыми Передача тепла к воде.
Ребра стальных цилиндров авиационного поршневого двигателя воздушного охлаждения выполнены толщиной около 1,0 мм и толщиной 20.It также выше на тангаже 4.0 mm. Глава. Цилиндр обычно снабжен алюминиевым ребром толщиной около 1,5 мм, высотой 35,6 галлонов и расстоянием между ребрами около 5,08 мм. Эти значения очень близки к оптимальным значениям. Его получают по формуле (3-35).Также на радиаторах водяного охлаждения имеются очень тонкие ребра (на высоте 5.08 мм-около 0.10-0.20 мм).
Стационарные теплообменники При установке толщина ребер будет более оптимальной, чем обычно, так как вес в этом случае не играет существенной роли. Ребристая труба экономайзера парового котла, 1.25〜 Толщина 4 мм, высота 13-25 мм, расстояние 13-20 мм. Трубы для системы водяного отопления обычно имеют ребра толщиной 1,0-2,5 мм и шагом 25-40 мм в высоту. 10-25 мм. Эффективность нервюры. Выражение (3-37) является математическим определением термина»эффективность ребер».
- Система передачи тепла является при необходимости следует рассмотреть 2 определения эффективности костной ткани. 1) эффективность по отношению к основанию области реберной кости при отсутствии области реберной кости. 2) эффективность таких Нервюры с бесконечным термальным conductivity. It понятно, что формула (3-37) является первой type. As в качестве примера приведем выражение, представляющее оба типа эффективности simple Прямоугольные ребра.
Бесконечно длинный край<3-3⁸) (3-39) ограниченный край/аСЛОМИ / и / / ОЛП \ ’ = — = vяth ¡ КПД к тому же ребро площади основания и Ф-бесконечная теплопроводность. Прямая кромка профиля треугольника. При определении оптимального ребра Возникает вопрос: Можно ли сэкономить вес, используя другие треугольные ребра, а не ранее рассмотренные ребра прямоугольного сечения? 3-10.Это отличное приложение. Форма поперечного сечения. Затем рассматривается прямой край сечения треугольника.
Такие ребра показаны на рисунке. 3-10.Математический анализ в этом случае является То же, что и для ребер прямоугольного сечения, за исключением примера, где площадь, перпендикулярная тепловому потоку, рассматривается как функция расстояния вдоль ребра длина реберной кости увеличивается и уменьшается.
Подставляя эти значения в уравнение (3-42), получаем: dx2’xx(3-43), где 0-температура окружающей среды и избыточная температура ребра относительно р. Людмила Фирмаль
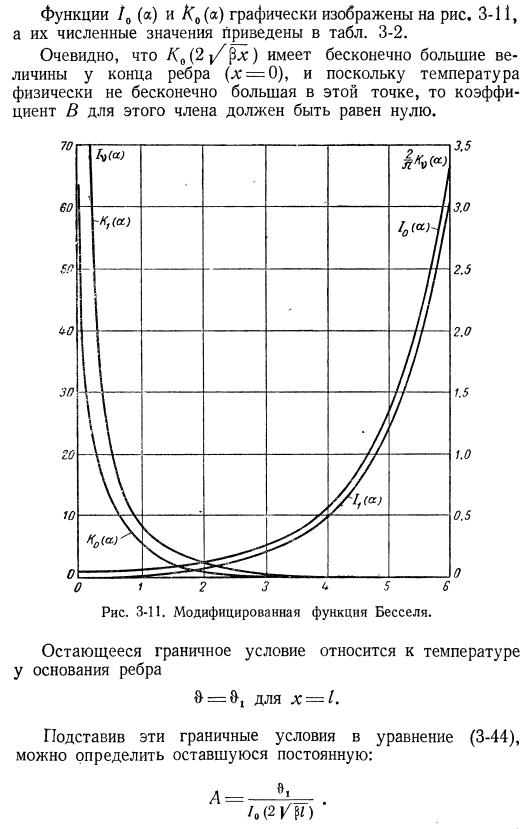
Поэтому дифференциальное уравнение, описываемое для постоянной теплопроводности и коэффициента теплопередачи, принимает вид:(3-42) 9 Площадь A (x) может быть выражена непосредственно в терминах, обозначающих отношение высоты ребра и длины x / 1:.Если a (x)= lL〜, L> 6, то периметр равен C = 2£. 2 «/ *ТТь ’ (3-43) — это не что иное, как модифицированное уравнение Бесселя [L. 7], форма его решения: & = a /₀(2 / ^)+5к, (2 /Р). (3-44) функция / ₀ (A) и к (a) показаны на рисунках. 3-11, а их номера приведены в таблице. 3-2.Очевидно, что f < ₀ (2i / px) имеет бесконечно большие значения в конце ребра (x = 0), и Коэффициент B этого члена должен быть равен нулю, потому что в этой точке температура физически не бесконечно велика.
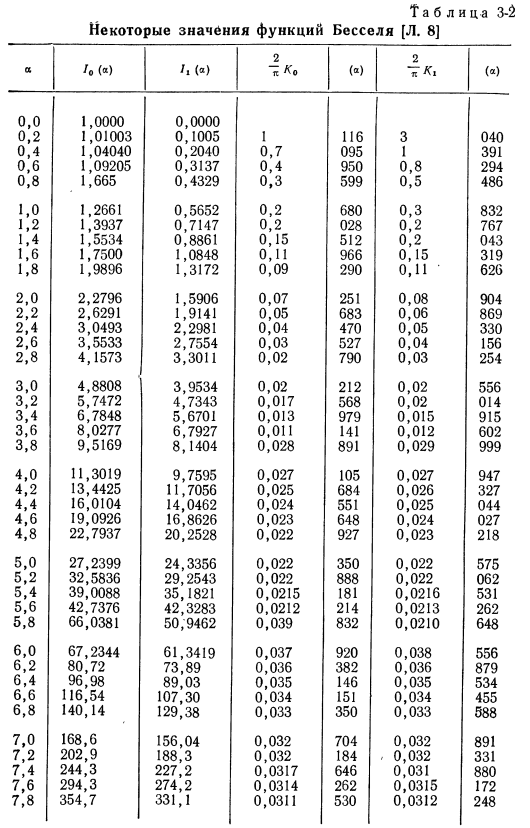
Рисунок 3-11.Изменена функция Бесселя. Остальной. Граничное условие относится к температуре= x = 1 в основании ребра. Оставшиеся константы можно определить, подставив эти граничные условия в выражение(от 3 до 44). Д ₌_ л > (2 / ₽ 0 * 3-2 таблица некоторых значений функции Бесселя [л. 8], а/о (») Л(а)2 (а) 2 («) 1КвТ*,0,0 1, 0000 0.0000 0.2 1.01003 0.1005 1 116 3 040 0.4 1.04040 0.2040 0.7 095 1 391 0.6 1.09205 0.3137 0.4 950 0.8 294 0、 8 1,665 0,4329 0,3 599 0.5 486 1.0 1.2661 0.5652 0.2 680 0.3 832 1.2 1.3937 0.7147 0.2 028 0.2 767 1.4 1.5534 0.8861 0、 15 512 0.2 043 1.6 1.7500 1.0848 О, а 966 0.15 319 1.8 1.9896 1.3172 0.09 290 o. i … 626 2.0 2.2796 1.5906 0.07 251 0.08 904 2.2 2.6291 1.9141 0.05 683 0 、06 869 2.4 3.0493 2.2981 0.04 470 0.05 330 2.6 3.5533 2.7554 0.03 527 0.04 156 2.8 4.1573 3.3011 0.02 790 0.03 254 3.0 4.8808 3.9534 0.02 212 0.02 556 3 2 5.7472 4.7343 0.017 568 0.02 014 3.4 6.7848
5.6701 0.013 979 0.015 915 3.6 8.0277 6.7927 0.011 141 0.012 602 3.8 9.5169 8.1404 0.028 891 0.029 999 4.0 11.3019 9.7595 0.027 105 0.027 947 4.2 13 4425 11.7056 0.025 684 0.026 327 4.4 16.0104 14.0462 0.024 551 0.025 044 4.6 19.0926 16.8626 0.023 648 0.024 027 4.8 22.7937 20.2528 0.022 927 0.023 218 5.0 27.2399 24 、3356 0.022 350 0.022 575 5.2 32.5836 29.2543 0.022 888 0.022 062 5.4 39.0088 35.1821 0.0215 181 0.0216 531 5.6 42.7376 42.3283 0.0212 214 0.0213 262 5 8 66.0381 50.9462 0.039 832 0.0210 648 6.0 67.2344 61.3419 0.037 920 0.038 556 6.2 80.72 73.89 0.036 382 0.036 879 6.4 96.98 89.03 0.035 146 0.035 534 6.6 116.54 107.30 0.034 151 0.034 455 6.8 140.14
129.38 0.033 350 0.033 588 7.0 168.6 156.04 0.032 704 0.032 891 7.2 202.9 188.3 0.032 1840.032 331 7.4 244.3 227.2 0.0317 646 0.031 880 7 6,294.3 274.2 0.0314 262 0.0315 172 7.8 354.7 331.1 0.0311 530 0.0312 248 tl 3-2 a 10 (a)/ 1 ( » ) 2 (a) 2 (a) I Co 8.0 427.6 399.9 0.049 325 0.049 891 8.2 515.6 483.0 0.047 543 0.047 991 8.4 621.9 583.7 0.046 104 0.046 458 8.6 750.5 705.4 0.044 941 0.045 220 8 8,905.8 852.7 0.044 000 0.044 221 9.0 1 093.6 1 030.9 0.043 239 0.043 415 9.2 1 320.7 1 246.7 0.042 624 0.042 763 9.4 1 595.3 1 507.9 0.042 126 0.042 236 9.6 1 927 1824 0.0417 226 0.041 810 9.8 2 329 2 207 0.0413 962 0.0414 658 10.0 0.0411 319 0.0411 872 уравнение распределения следовательно, температура будет окончательной.
Следующим образом: ft. «.(2 на «(3-45) интенсивность теплового потока diQ (a.) Lda.=Д(а):(3-46) Если тепловой поток падает на край треугольного сечения при оптимальных условиях, оптимальное соотношение 1 / b может быть выражено следующим образом: u =1 — ⁰ ⁰⁹⁹ / § — (з — ⁴⁷ ) Избыточная температура в верхней части ребер 03 = 0,2770. (3-48) отношение толщины ребра прямоугольного сечения к толщине ребра треугольного сечения к тому же тепловому потоку составляет、 1.31; отношение площади поперечного сечения составляет 1:1.44.As в результате, используя 3 ребра треугольного сечения, можно сэкономить до 44% материала.
Ребра с минимальным весом (л. 9.、 10].Тогда будет интересно определить оптимальную форму поперечного сечения ребра с минимальным весом (потоком) для заданной величины теплоты. Он должен быть использован с таким же коэффициентом полезного действия. То есть определенный тепловой поток должен оставаться постоянным по всему поперечному сечению ребра. Это свидетельство (е. оно было предоставлено Шмидтом.
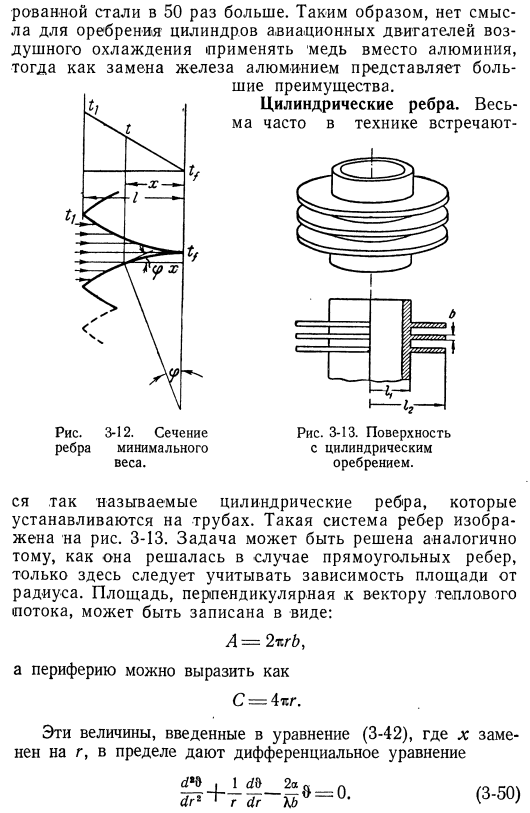
Такая кромка тепловых линий тока должна иметь форму, показанную на рисунке. 3-12.Они представляют собой ряд прямых линий, расположенных на равном расстоянии друг от друга, параллельно оси ребра. С константой — Тепловой поток, температура которого изменяется вдоль линии теплового потока по линейному закону от температуры т \на дне ribs. It необходимо проверить температуру в верхней части Ребра не сильно отличались от температуры окружающего газа.
Изменение температуры внутри ребра показано в верхней части рис. 3-12.At расстояние x от вершины ребер, температура благодаря равномерности температурного поля, равной t, разность между температурой t и температурой газа tf может быть выражена как: тепловой поток вдоль оси ребра q. рассмотрим элементы реберной поверхности на расстоянии x. эта площадь поверхности является осью реберной кости и углом cp. In в этом случае тепловой поток через поперечное сечение равен q sin 4i назад Она пропорциональна величине теплопроводности Л. Так что вес пропорционален Р / х. В таблице. 3-3 показано отношение плотности p к значению коэффициента теплопроводности Z.
Для разнообразия materials.It следует отметить, что использование алюминия вместо меди снижает массу на 50%.Вес нервюр литого железа 10, и вес нервюр 3-3 теплопроводность-график-r / x, P / 1 материал nost X, nost p, h-кг>град (па)д | ккал! м-х-г! см9. ккал} * * медь……….. 327 8.965 27.4 1.96 чистый алюминий….. 193 2.722 14.0 1.00 алюминиевый сплав…… Сто тридцать четыре 2.658 20.0 1.42 чистый магний.. Что?.. 149 1.761 14.0 1.01 сталь……… 48 7.845 164.5 11.80 нержавеющая сталь…. 12 7.845 658.0 47.10 сталь более чем в 50 раз. Поэтому » нет смысла использовать медь вместо меди.» Больно заменять алюминий, железо на алюминий. 3-12.Поперечное сечение ребер с минимальным весом. Свои преимущества. Цилиндрические ребра. Рис часто встречается в технике.
3-13.Поверхность с цилиндрическим ребром. Это так называемые цилиндрические ребра, которые крепятся к трубе. Такая система ребер показана на рисунке. 3-13.Задача такая Она решается так же, как решалась в случае прямоугольного ребра, только здесь необходимо учитывать зависимость от радиуса области. Площадь, перпендикулярная вектору тепла (Поток, а = 2m. it могут быть записаны в виде bb и окружения C-4g. могут быть выражены как G. эти величины вводятся в Формулу (3-42).
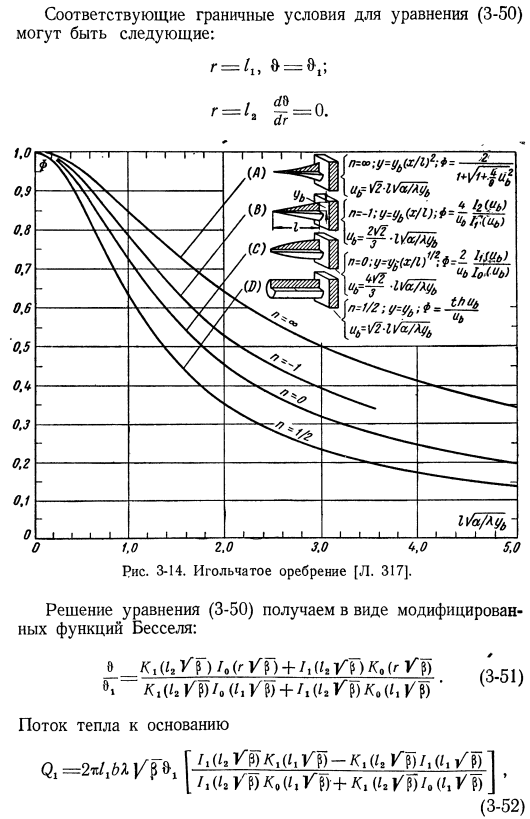
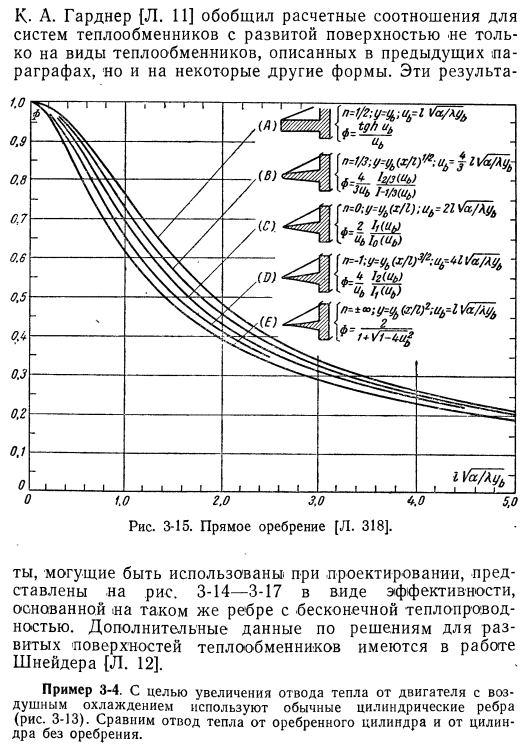
Пределы дают дифференциальные уравнения d * b I 1 db 2а zsdr ^ VTr (3-50) граничные условия, соответствующие уравнению (3-50) являются: Получаем выражение (3-50) в виде функции Фикса-Бесселя., k, (I, U p l>(<I)+ L u, UN k, (rO»3-51) тепловой поток к основанию (3-52) К. А. Гарднер. 11.] Мы обобщили расчетное отношение теплообменных систем с развитыми поверхностями не только к типам теплообменников, описанным в предыдущем параграфе, но и к некоторым другим формам.
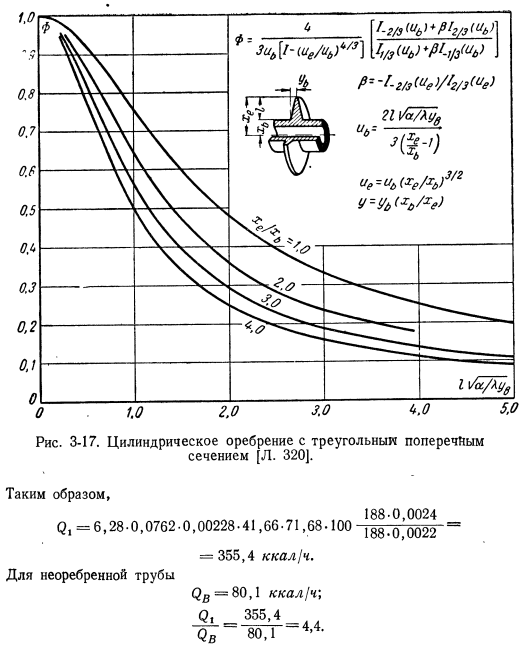
На рисунках показаны эти результаты, которые могут быть использованы при проектировании.3. в виде КПД на основе тех же ребер с бесконечной теплопроводностью-14-3-17 нет. Дополнительные данные о разработанном решении бета-поверхности теплообменника можно найти в статье Schneider {L. 12].Пример 3-4.To увеличьте тепловыделение от двигателя с воздухом Для охлаждения используются обычные цилиндрические ребра (рис. 3-13).
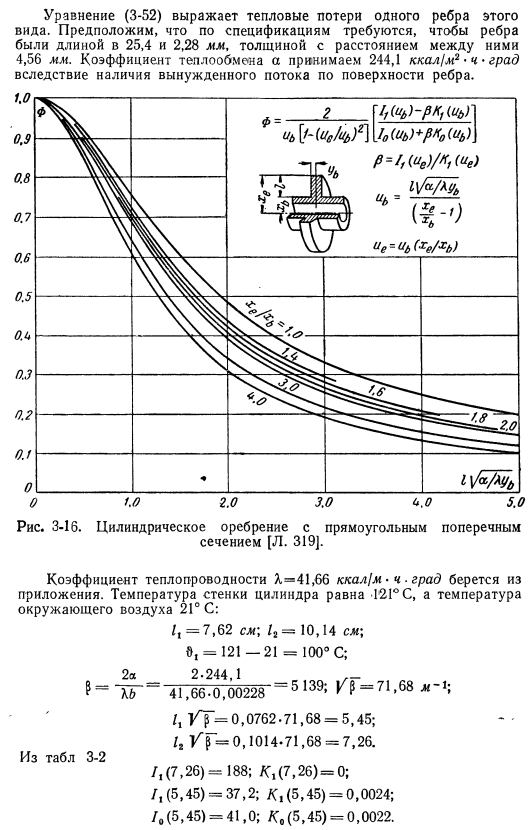
Сравните тепловыделение от ребристого цилиндра к тому от ребристого цилиндра. Формула (3-52) представляет потери тепла Вот такие ребрышки. Предположим, в спецификациях длина ребер должна составлять 25,4 мм и 2,28 мм, а толщина между ними-4,56 мм. Коэффициент теплопередачи в Принимают 244,1 ккал / м2•ч * аил. Это связано с наличием принудительного течения на поверхности реберной кости. Рисунок 3-16.Цилиндрические ребра прямоугольного сечения[л. 319]. Коэффициент теплопроводности х = 41,66 ккал 1м * ч град получается из приложения.
Температура стенки цилиндра составляет 121 ° C, температура окружающей среды-21°C:/ₜ= 7,62 см \ / ₂ = 10.14 \ см «= 121-21 = 100°с; 2а 2-244. 1 0 = xb-41 66-0. 00228 «⁵13⁹<» к? 71.68 промилле; /, о, 0762.71.68 = 5.45;/ / Ф = 0.1014-71.68 = 7.26. /,(7.26)= 188; к(7.26) = 0; /、(5.45)= 37.2; К(5.45)= 0.0024; / О(5.45)= 41.0; Ко(5.45)= 0.0022.Из таблицы 3-2, Q= 6.28-0.0762-0.00228-41.66-71.68-100 = 355,4 ккал, 4.Для труб без ребер QB = 80, л ккал! Ч \ 188-0. 0024 188-0. 0022 Вопрос, 355.4 Qb80.14.4.
Смотрите также:
| Критическая толщина изоляции | Стенка с внутренним источником тепла |
| Тонкий стержень | Подземный кабель |

