Развертки поверхностей
Разверткой называется плоская фигура, в которую преобразуется поверхность предмета при ее совмещении с плоскостью. При этом подразумевается, что поверхность — это гибкая, но нерастяжимая и несжимаемая пленка и при ее развертке не происходит разрывов и образования складок.
Поверхности, которые допускают такое преобразование, называются развертывающимися.
К развертывающимся поверхностям относятся многогранники и некоторые линейчатые поверхности — цилиндрические, конические и поверхности с ребром возврата (торсы — развертка торсов не рассматривается).
Развертки можно построить точные и приближенные.
Точные развертки можно строить для гранных поверхностей призмы и пирамиды (не считая графических погрешностей построения), для круговых цилиндров (развертка — прямоугольник с размерами (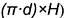 ) и круговых конусов (круговой сектор с углом
) и круговых конусов (круговой сектор с углом 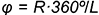 , где
, где 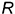 — радиус основания конуса;
— радиус основания конуса; 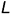 — длина его образующей).
— длина его образующей).
Развертки, которые можно построить графически, заменяя (аппроксимируя) заданные поверхности участками развертывающихся призматических, пирамидальных или цилиндрических поверхностей, называются приближенными. К поверхностям, развертку которых можно построить приближенно, относятся круговые наклонные конуса, эллиптические цилиндры с круговыми сечениями, сферические, торовые, а также комбинированные поверхности, участки которых состоят из развертывающихся поверхностей.
Каждой точке на поверхности соответствует единственная точка на развертке, т. е. между поверхностью и ее разверткой существует взаимно однозначное соответствие, которое обладает следующими основными свойствами:
- а) длины соответствующих линий на поверхности и на развертке равны;
- б) линии, параллельные на поверхности, сохраняют параллельность на развертке;
- в) углы между соответствующими пересекающимися линиями на поверхности и на развертке равны;
- г) площади соответствующих фигур на поверхности и на развертке, ограниченные замкнутыми линиями, равны.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Торовая поверхность — тор |
| Пересечение поверхностей и способы построения линий пресечения |
| Развертка поверхности пирамиды |
| Развертка поверхности призмы |

