Развертка сферической поверхности
На рис. 9.9 показано построение условной развертки сферической поверхности.
Поверхность сферы условно разрезают на ка-кое-то количество частей (6, 12 и более) и каждую часть заменяют (аппроксимируют) цилиндрической описанной поверхностью, фронтальная проекция которой совпадает с фронтальным очерком сферы — окружностью.
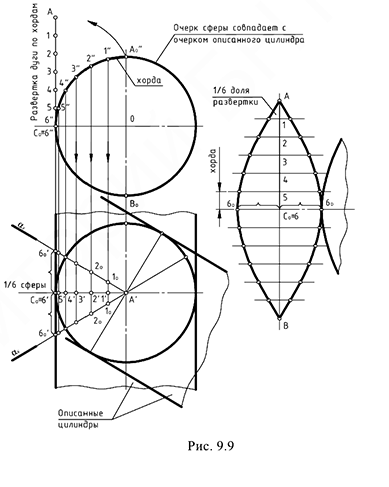
Далее выполнятся развертка одной доли поверхности сферы как сектора цилиндрической поверхности по следующему графическому алгоритму:
1-е действие. На горизонтальной проекции разрезать поверхность сферы на 6 частей и рассмотреть эту 1/6 часть (сектор) как фронтально-проецирующий цилиндр, описанный вокруг сферы.
2-е действие. Разделить дугу очерковой окружности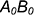 
сферы, которая совпадает с окружностью описанного цилиндра, на 12 частей (поскольку есть симметрия, рассматриваем дугу 
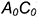) и заменить участки хордами (то есть вписать 12-угольную призму) — 
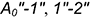и т. д.
3-е действие. Спроецировать точки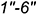 
на стороны взятого сектора его горизонтальной проекции.
4-е действие. Свободном поле чертежа провести вертикальную линию и отложить от точки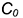 
вверх и вниз по 6 отрезков, равных величине хорд (точки пронумеровать).
5-е действие. Через каждую построенную точку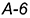 
провести горизонтальные линии и на каждой отложить величину соответствующей образующей: 
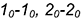и т. д.
6-е действие. Конечные точки соединить лекальной кривой.
Таким образом построена 1/6 доля условной поверхности сферы, а 6 таких долей составят развертку всей поверхности.
С увеличением количества долей (1/12, 1/24 и т. д.) точность развертки увеличивается.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Развертка кругового цилиндра |
| Развертка кругового конуса |
| Аксонометрические проекции |
| Развертка поверхности открытого тора |
