Развертка поверхности пирамиды
Построение развертки боковой поверхности пирамиды по натуральным величинам ее ребер выполняется по следующему графическому алгоритму.
1-е действие. Построить на заданных проекциях пирамиды натуральные величины всех ее боковых ребер (например, способом вращения вокруг проецирующей прямой) и натуральные величины сторон многоугольника основания пирамиды (если основание лежит в плоскости уровня, то натуральные величины даны на одной из проекций).
2-е действие. Построить на свободном поле чертежа последовательно грани пирамиды по натуральным величинам ребер и натуральным величинам сторон основания (с помощью дуг-засечек) так, чтобы они имели общую вершину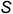 
и примыкали друг к другу.
3-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам пирамиды тонкими штрихпунктирными линиями.
На рис. 9.3 показан пример построения развертки поверхности правильной треугольной пирамиды, основание которой треугольник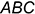 
на горизонтальной проекции имеет натуральные величины сторон, так как лежит в горизонтальной плоскости уровня.
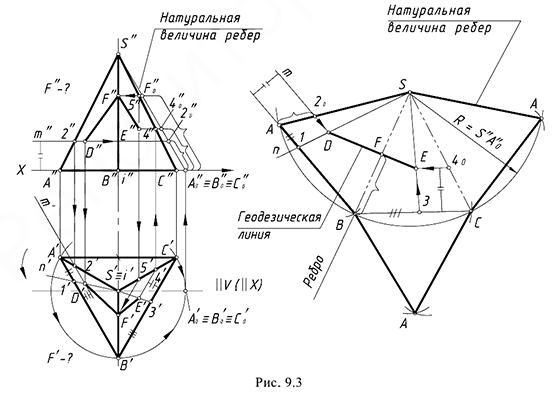
Для построения развертки выполнены графические действия предложенного алгоритма.
1-е действие. Построить на заданной фронтальной проекции натуральные величины ребер пирамиды способом вращения вокруг горизонтально-проецирующей оси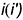 
, проходящей через вершину пирамиды точку 
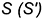и совпадающую с ее высотой. Напоминаем графические действия этого способа преобразования:
1.1. Повернуть горизонтальные проекции ребер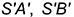 
и 
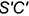вокруг оси 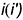так, чтобы они расположились параллельно фронтальной плоскости проекций 
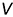(все ребра правильной пирамиды равны по длине), и получить совмещенные проекции точек 
.
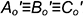1.2. На фронтальной проекции пирамиды конечные точк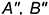и 
и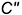 
ребер перемещаются по горизонтальной линии, перпендикулярной оси 
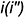, и на пересечении с линией связи от точек 
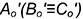построить точки 
.
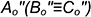1.3. Соединить вершину пирамиды 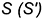с совпадающими точками 
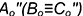— полученный отрезок 
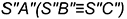и есть натуральная величина всех ребер пирамиды.
2-е действие. На свободном поле чертежа построить последовательно (например, против часовой стрелки) от ребра 
, по которому «разрезается» поверхность, треугольники граней пирамиды с общей вершиной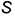 
следующим образом:
2.1. Провести дугу радиусом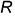 
равным натуральной величине ребер 
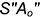пирамиды из произвольной точки 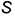плоскости чертежа.
2.2. На дуге отметить (произвольно) вершину основания точку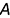 
, то есть построить ребро пирамиды.
2.3. На проведенной дуге засечками, равными длине сторон основания пирамиды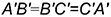 
отметить следующие точки вершин основания -в, С и точку А.
2.4. Построить треугольники граней пирамиды, соединив вершину 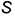с вершинами основания и достроить основание пирамиды к стороне, например, 
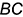грани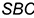 
.
3-е действие. Оформить чертеж развертки, выполнив линии сгиба по ребрам пирамиды тонкими штрихпунктирными линиями с двумя короткими пунктирами.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Развертки поверхностей: общие сведения |
| Развертка поверхности призмы |
| Развертка кругового цилиндра |
| Развертка поверхности геодезической линии |
