Геодезическая линия
Геодезическая линия — это линия кратчайшего расстояния между двумя точками на поверхности. На развертке этой линии соответствует прямая. Геодезическая линия строится на развертке по двум ее конечным точкам, заданным на проекциях предмета, а затем достраивается на заданных проекциях по дополнительным промежуточным точкам, взятым на построенной развертке.
На рис. 9.3 показано построение проекций геодезической линии на поверхности пирамиды по двум заданным на проекциях конечным точкам 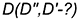 и
и 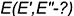 .
.
Порядок графических действий для построения геодезической линии:
1-е действие. Построить полную развертку поверхности (в данном примере развертка пирамиды уже построена).
2-е действие. Построить на развертке геодезическую линию.
2.1. Построить на развертке заданные точки 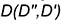 и
и 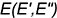
- точка
 определяется на развертке на пересечении вспомогательной линии
определяется на развертке на пересечении вспомогательной линии 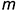 , проведенной параллельно стороне
, проведенной параллельно стороне 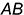 основания на расстоянии
основания на расстоянии 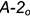 , равным отрезку
, равным отрезку 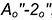 , взятому на построенной натуральной величине ребер и отложенному по ребру
, взятому на построенной натуральной величине ребер и отложенному по ребру  развертки, и линии, проведенной через точку
развертки, и линии, проведенной через точку 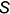 и точку 1, построенную на стороне
и точку 1, построенную на стороне 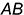 развертки по отрезку
развертки по отрезку 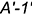 , взятому на горизонтальной проекции
, взятому на горизонтальной проекции  стороны основания;
стороны основания; - точка
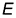 определяется на пересечении аналогично построенных линий
определяется на пересечении аналогично построенных линий 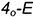 и
и 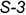 ;
;
2.2. Соединить построенные на развертке точки геодезической линией 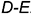 , которая пересекает ребро
, которая пересекает ребро  в точке
в точке 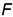 .
.
3-е действие. Достроить фронтальную и горизонтальную проекции геодезической линии 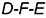 на проекциях пирамиды по промежуточной точке
на проекциях пирамиды по промежуточной точке 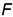 с учетом видимости линии на поверхности (на проекциях пирамиды проекции геодезической линии — ломаные линии):
с учетом видимости линии на поверхности (на проекциях пирамиды проекции геодезической линии — ломаные линии):
3.1. Отрезок 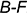 , взятый на развертке (отмечен скобкой), отложить на натуральной величине ребер, построенных на фронтальной проекции, и определить положение точки
, взятый на развертке (отмечен скобкой), отложить на натуральной величине ребер, построенных на фронтальной проекции, и определить положение точки 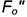 .
.
3.2. Провести через точку 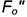 линию, параллельную основанию пирамиды, и на пересечении с проекцией ребра
линию, параллельную основанию пирамиды, и на пересечении с проекцией ребра 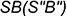 построить фронтальную проекцию точки
построить фронтальную проекцию точки 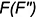 геодезической линии.
геодезической линии.
3.3. Достроить горизонтальную проекцию точки 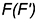 по вспомогательной точке
по вспомогательной точке 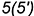 , лежащей на ребре
, лежащей на ребре 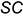 .
.
3.4. Соединить на проекциях пирамиды заданные проекции точек 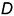 и
и 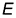 с построенной точкой
с построенной точкой 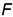 , определив видимость участков ломаной геодезической линии.
, определив видимость участков ломаной геодезической линии.
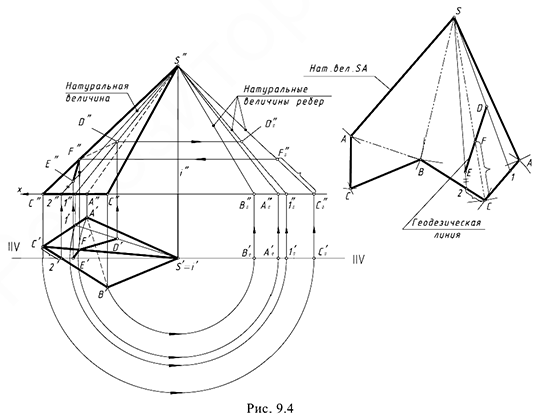
На рис. 9.4 показан пример построения развертки неправильной треугольной пирамиды  и геодезической линии
и геодезической линии 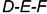 на развертке и на проекциях пирамиды по заданным конечным точкам
на развертке и на проекциях пирамиды по заданным конечным точкам 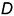 и
и 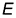 . Основание пирамиды лежит в горизонтальной плоскости и на горизонтальной проекции пирамиды стороны основания имеют натуральную величину.
. Основание пирамиды лежит в горизонтальной плоскости и на горизонтальной проекции пирамиды стороны основания имеют натуральную величину.
Построение развертки поверхности пирамиды выполнено по приведенному выше алгоритму с дополнительными графическими действиями по построению геодезической линии:
1-е действие. Построить на фронтальной проекции пирамиды способом вращения вокруг горизонтально-проецирующей оси 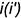 , проходящей через вершину пирамиды
, проходящей через вершину пирамиды 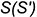 , натуральные величины всех ребер пирамиды и вспомогательной линий
, натуральные величины всех ребер пирамиды и вспомогательной линий 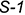 , проведенной на грани пирамиды
, проведенной на грани пирамиды 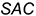 через заданную точку
через заданную точку  , и определить проекцию
, и определить проекцию 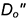 точки
точки  на натуральной величине
на натуральной величине 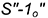 вспомогательной линии
вспомогательной линии 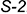 : вспомогательная линия
: вспомогательная линия 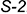 , проведенная через точку
, проведенная через точку 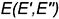 , является фронтальной
, является фронтальной 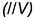 , и проекция
, и проекция 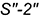 есть ее натуральная величина, которую можно использовать для построения точки
есть ее натуральная величина, которую можно использовать для построения точки 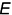 на развертке.
на развертке.
2-е действие. Построить на свободном поле чертежа последовательно от ребра  по часовой стрелке треугольники граней пирамиды с общей вершиной
по часовой стрелке треугольники граней пирамиды с общей вершиной 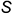 по натуральным величинам ее ребер и сторон основания дугами-засечками соответствующей величины и достроить основание пирамиды к стороне
по натуральным величинам ее ребер и сторон основания дугами-засечками соответствующей величины и достроить основание пирамиды к стороне  .
.
3-е действие. Оформить чертеж развертки, проведя линии сгиба.
4-е действие. Построить геодезическую линию на развертке и заданных проекциях пирамиды.
4.1. Построить на развертке конечные точки 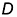 и
и  на вспомогательных линиях
на вспомогательных линиях 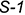 и
и 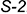 по натуральным величинам отрезков
по натуральным величинам отрезков 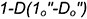 и
и 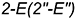 и соединить эти точки прямой геодезической линией
и соединить эти точки прямой геодезической линией 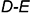 , которая пересекает ребро
, которая пересекает ребро 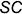 в точке
в точке 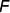 .
.
4.2. Достроить фронтальную и горизонтальную проекции ломаной геодезической линии 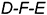 на проекциях пирамиды с учетом ее видимости, определив проекции точки
на проекциях пирамиды с учетом ее видимости, определив проекции точки 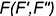 на ребре
на ребре 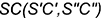 по ее положению на развертке (по отрезку
по ее положению на развертке (по отрезку 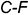 ).
).
Приближенные развертки цилиндрических и конических поверхностей
Развертки цилиндрических и конических поверхностей выполняются аналогично разверткам призматических и пирамидальных поверхностей. При этом цилиндрическая поверхность заменяется (аппроксимируется) вписанной многоугольной призматической поверхностью (обычно 12-угольной), а коническая поверхность заменяется вписанной многоугольной пирамидальной поверхностью, т. е. строятся приближенные развертки.
Эта теория взята со страницы лекций для 1 курса по предмету «начертательная геометрия»:
Начертательная геометрия для 1 курса
Возможно эти страницы вам будут полезны:
| Развертка поверхности призмы |
| Развертка поверхности пирамиды |
| Развертка кругового конуса |
| Развертка кругового цилиндра |

