Оглавление:
Разложение вектора по ортам координатных осей. Модуль вектора. Направляющие косинусы
Рассмотрим в пространстве прямоугольную систему координат 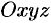 . Выделим на координатных осях
. Выделим на координатных осях 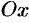 ,
, 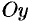 и
и 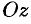 единичные векторы (орты), обозначаемые
единичные векторы (орты), обозначаемые 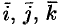 соответственно (см. рис. 12).
соответственно (см. рис. 12).
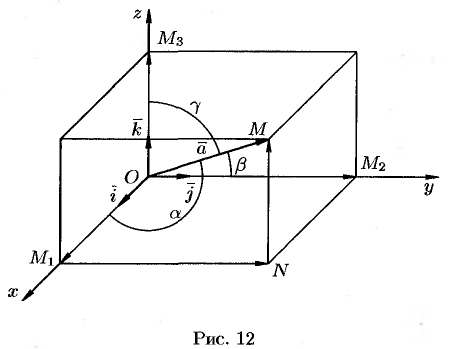
Выберем произвольный вектор 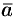 пространства и совместим его начало с началом координат:
пространства и совместим его начало с началом координат: 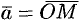 .
.
Найдем проекции вектора 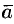 на координатные оси. Проведем через конец вектора
на координатные оси. Проведем через конец вектора 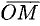 плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через
плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через 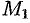 ,
, 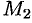 и
и 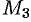 . Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор
. Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор 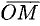 . Тогда
. Тогда 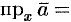
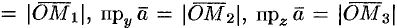 . По определению суммы нескольких векторов находим
. По определению суммы нескольких векторов находим 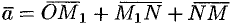 .
.
А так как 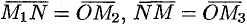 , то
, то
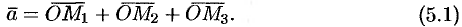
Но
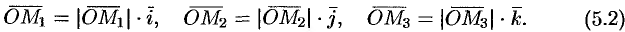
Обозначим проекции вектора 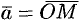 на оси
на оси 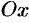 ,
, 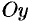 и
и 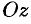 соответственно через
соответственно через 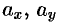 и
и 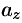 , т. е.
, т. е. 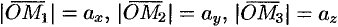 . Тогда из равенств (5.1) и (5.2) получаем
. Тогда из равенств (5.1) и (5.2) получаем
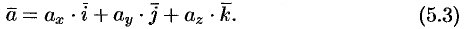
Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных oсей.
Числа 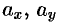 ,
, 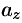 называются координатами вектора
называются координатами вектора 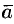 , т. е. координаты вектора есть его проекции на соответствующие координатные оси.
, т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство (5.3) часто записывают в символическом виде: 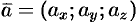 .
.
Равенство 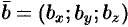 означает, что
означает, что 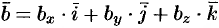 .
.
Зная проекции вектора 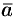 , можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать
, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать 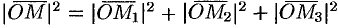 , т. е.
, т. е.

Отсюда
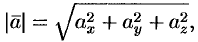
т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть углы вектора 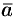 с осями
с осями 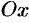 ,
, 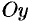 и
и 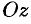 соответственно равны
соответственно равны 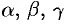 . По свойству проекции вектора на ось, имеем
. По свойству проекции вектора на ось, имеем
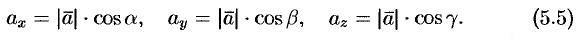
Или, что то же самое,
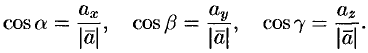
Числа 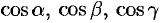 называются направляющими косинусами вектора
называются направляющими косинусами вектора 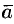 .
.
Подставим выражения (5.5) в равенство (5.4), получаем
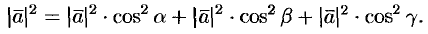
Сократив на 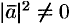 , получим соотношение
, получим соотношение
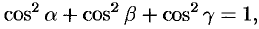
т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора 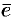 являются числа
являются числа 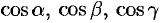 , т. е.
, т. е. 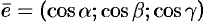 .
.
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т. е. сам вектор.
Действия над векторами, заданными проекциями
Пусть векторы 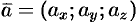 и
и 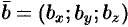 заданы своими проекциями на оси координат
заданы своими проекциями на оси координат  ,
,  ,
,  или, что то же самое
или, что то же самое
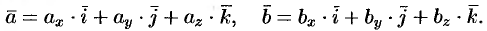
Линейные операции над векторами
Так как линейные операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:
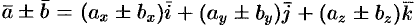 , или кратко
, или кратко 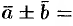
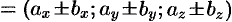 . То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).
. То есть при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются).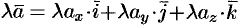 или короче
или короче 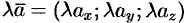 . То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
. То есть при умножении вектора на скаляр координаты вектора умножаются на этот скаляр.
Равенство векторов
Из определения вектора как направленного отрезка, который можно передвигать в пространстве параллельно самому себе, следует, что два вектора 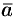 и
и 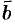 равны тогда и только тогда, когда выполняются равенства:
равны тогда и только тогда, когда выполняются равенства: 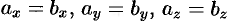 , т. е.
, т. е.
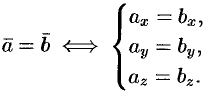
Коллинеарность векторов
Выясним условия коллинеарности векторов 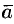 и
и 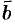 , заданных своими координатами.
, заданных своими координатами.
Так как 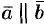 , то можно записать
, то можно записать 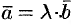 , где
, где 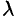 — некоторое число. То есть
— некоторое число. То есть
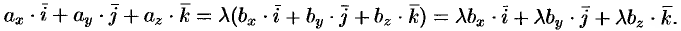
Отсюда
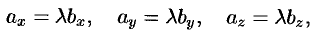
т.е.
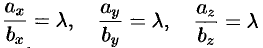 или
или 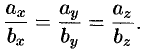
Таким образом, проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: векторы, имеющие пропорциональные координаты, коллинеарны.
Координаты точки
Пусть в пространстве задана прямоугольная декартова система координат 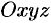 . Для любой точки
. Для любой точки 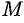 координаты вектора
координаты вектора 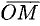 называются координатами точки
называются координатами точки 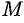 . Вектор
. Вектор 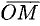 называется радиус-вектором точки
называется радиус-вектором точки 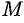 , обозначается
, обозначается 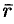 , т. е.
, т. е. 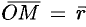 . Следовательно, координаты точки — это координаты ее радиус-вектора
. Следовательно, координаты точки — это координаты ее радиус-вектора
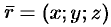 или
или 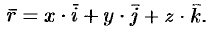
Координаты точки  записываются в виде
записываются в виде  .
.
Координаты вектора
Найдем координаты вектора 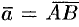 , если известны координаты точек
, если известны координаты точек 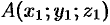 и
и 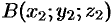 . Имеем (см. рис. 13):
. Имеем (см. рис. 13):
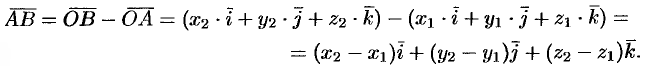
Следовательно, координаты вектора равны разностям соответствующих координат его конца и начала: 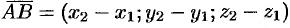 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Линейные операции над векторами |
| Проекция вектора на ось |
| Скалярное произведение векторов и его свойства |
| Выражение скалярного произведения через координаты |

