Оглавление:

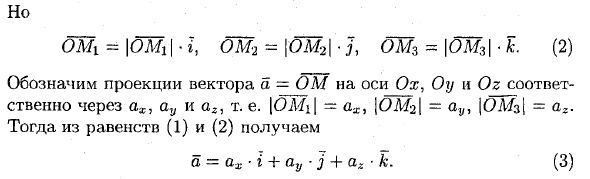


Разложение вектора по ортам координатных осей. Модуль вектора направляющие косинусы
- Vector Decomposition Векторный модуль-гид по Орте координатной оси Рассмотрим ортогональную систему координат Oxyz в пространстве. На координатных осях Ox, Oy и Oz выберите единичные векторы (единичные векторы), обозначенные i, j и k соответственно (см. Рисунок). Z магнитный азимут M2 в Выберите произвольный вектор a в пространстве и объедините его начало с началом: a = OM. Найти проекцию вектора а на оси.
Проведите через края плоскости вектора ОМ параллельно плоскости координат. Получает кубоид, диагональ которого является вектором ОМ. Тогда prx a = | OMi [, a = \ OM2 \ и т. Д., A = \ bM3 . Определение суммы нескольких векторов находит a = OM \ + M \ N + NM. А так как M \ N = OM2, NM = OM3, (1) a = 0 Mi + bM2 4- bM2.
Пересечения этих плоскостей и осей обозначены Mi, M2 и M3 соответственно. Людмила Фирмаль
но OMi = IОMl | t, OM-2 = \ 0M2 \ • J, O M3 = \ OM31. (2) Вектор а = ось ОМ Ох, О? Проекции на / и Oz выражаются как ax, ay и a2 соответственно. То есть | OMi | = ah, IOM2I = ay, | OL / s | = a * -Тогда получаем из уравнений (1) и (2) a = ah • x + ay • j + az • k (3) Эта формула является основной формулой для векторных вычислений и называется векторным расширением на единичный вектор осей. Числа ax, ay и az называются координатами вектора a.
То есть координаты вектора являются проекциями на соответствующие координатные оси. Векторное уравнение (3) часто записывается в символической форме: a = {ax \ ay \ zz). , Уравнение b = (bx \ by \ b2) означает b-bx • i -f через • j 4-b2 • k. Если вам известна проекция вектора a, вы можете легко найти выражение для векторного модуля.
| Векторы и линейные операции над ними | Действия над векторами, заданными проекциями |
| Проекция вектора на ось | Скалярное произведение векторов и его свойства |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- На основании теоремы о диагональной длине кубоида можно записать: \ (Ш \ 2 = | ОМ \ | 2 + | ОМ2 | 2 + | ОМ3 | 2, т.е. \ a \ ^ al + al + al (4) Отсюда a | = yja’i + al + a *, Другими словами, модуль вектора равен квадратному корню из суммы квадратов проекции координатных осей 7ta. Сделайте угол вектора a с осями Ox, Oy и Oz равным o, / 3,7. Согласно свойству проецирования вектора на ось, ax = | a | • cos a, ay = | a | • cos / 3, az = | a | (5) Или то же самое Ах ах ах COS O = -, COS /) = 7Z7, cos 7 = -. \ a \ \ a ] a | Число cos или cos / 3, cos7 называется направленным косинусом вектора a.
Подставляя уравнение (5) в уравнение (4), | a | 2 = \ a \ 2 • cos2 a + | a | 2 • cos2,3 4- | a | 2 • cos2 7. Получить уменьшенный коэффициент 0
cos2 a + cos2 p -f cos2 7 = 1 Другими словами, сумма квадратов индукционного косинуса ненулевого вектора равна 1. Легко видеть, что координатами единичного вектора e являются числа cos a, cos cos 7, то есть e = (cos a; cos / 3; cos 7). Таким образом, установка координат вектора всегда определяет его модуль и направление, то есть сам вектор.

