Оглавление:
Разложение в ряд Фурье функций произвольного периода
Разлагать в ряд Фурье можно и периодические функции с периодом, отличным от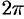 
.
Пусть функция 
, определенная на отрезке 
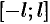, имеет период 
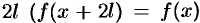, где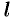 
— произвольное положительное число) и удовлетворяет на этом отрезке условиям Дирихле.
Сделав подстановку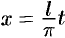 
, данную функцию преобразуем в функцию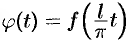 
, которая определена на отрезке 
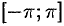и имеет период 
.
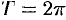Действительно, если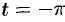 
, то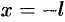 
, если 
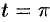, то 
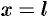и при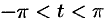 
имеем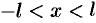 
;
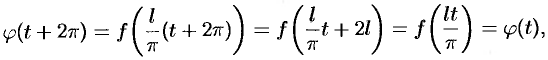
т. е.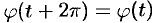 
.
Разложение функции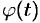 
в ряд Фурье на отрезке 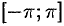имеет вид
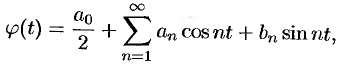
где
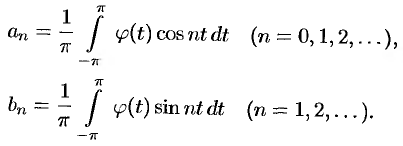
Возвращаясь к переменной 
и заметив, что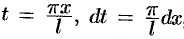 
, получим
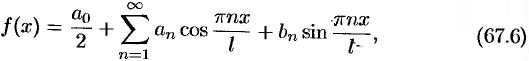
где
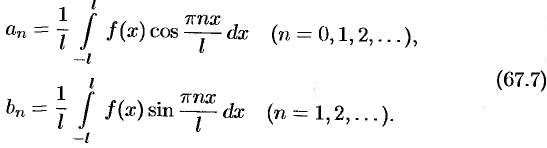
Ряд (67.6) с коэффициентами, вычисляемыми по формулам (67.7), называется рядом Фурье для функции с периодом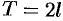 
.
Замечание. Все теоремы, имеющие место для рядов Фурье 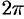-периодических функций, остаются в силе и для рядов Фурье функций, период которых 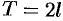. В частности, если на отрезке 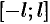четная, то ее ряд Фурье имеет вид
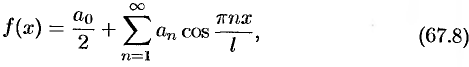
где
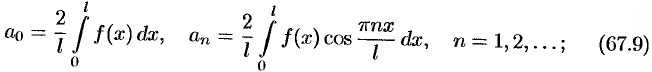
если — нечетная функция, то
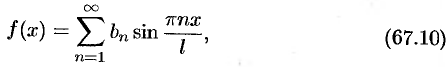
где
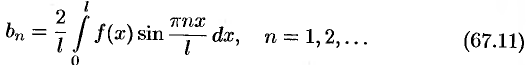
Пример №67.3.
Разложить функцию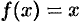 
на интервале (-4;4) и ряд Фурье.
Решение:
Данная функция нечетная, удовлетворяет условиям Дирихле. По формулам (67.10) и (67.11), при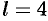 
, имеем:
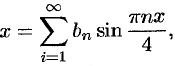
где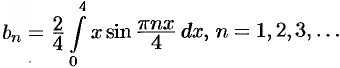 
Вычисляем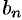 
:
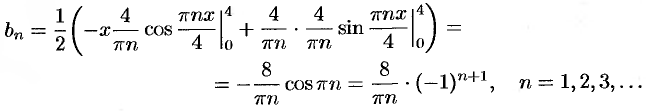
Таким образом,
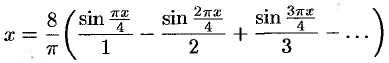
для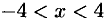 
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Тригонометрический ряд Фурье |
| Разложение в ряд Фурье четных и нечетных функций |
| Представление непериодической функции рядом Фурье |
| Комплексная форма ряда Фурье |
