Оглавление:
Разложение в ряд Фурье четных и нечетных функций
Если разлагаемая на отрезке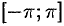 
в рад Фурье функция 
является четной или нечетной, то это отражается на формулах коэффициентов Фурье (вычисление их упрощается) и на виде самого ряда (он становится так называемым неполным).
Если функция четная, то ее ряд Фурье имеет вид
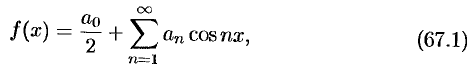
где
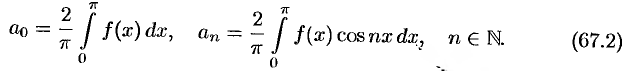
Если функция нечетная, то ее ряд Фурье имеет вид
где
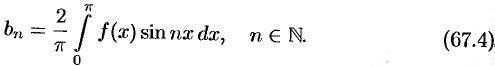
Как известно (см. п. 39.4), если функция интегрируема на симметричном отрезке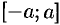 
, то
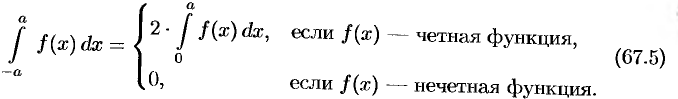
Если функция — четная, то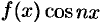 
— четная функция (
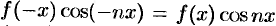), a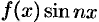 
— нечетная функция (
).
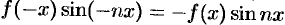Если же — нечетная функция, то, очевидно, функция 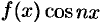— нечетная, a 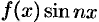— четная.
С учетом формулы (67.5) из формул (66.13) — (66.15) получаем формулы (67.1) — (67.4).
Ряды (67.1) и (67.3) называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам соответственно.
Пример №67.2.
Разложить в ряд Фурье функцию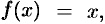 
.
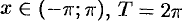Решение:
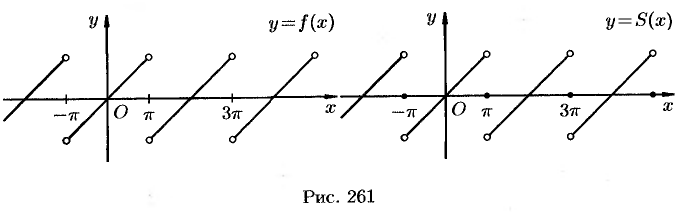
На рисунке 261 изображен график заданной функции. Условиям Дирихле функция 
удовлетворяет. Эта функция — нечетная. Следовательно, 
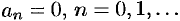, а
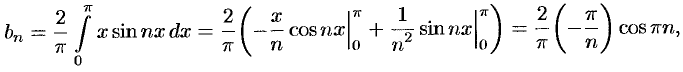
т. е.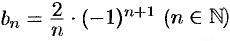 
. Ряд Фурье содержит только синусы:
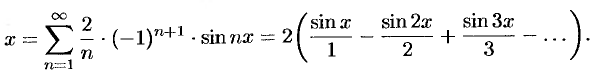
При этом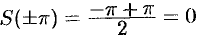 
(см. рис. 261).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Способ неопределенных коэффициентов |
| Тригонометрический ряд Фурье |
| Разложение в ряд Фурье функций произвольного периода |
| Представление непериодической функции рядом Фурье |
