Оглавление:




Разложение уравнения изогнутой оси в тригонометрический ряд.
- Разложение уравнения кривой оси на ряд тригонометрических функций. Метод замены изогнутой оси балки одной синусоидой, описанный в предыдущем пункте, является таким удовлетворительным решением во всех случаях нагрузки, как
в рассмотренном примере. В этих случаях желательно представить криволинейную ось луча в виде суммы ряда синусоид, то есть разложить уравнения криволинейной оси в бесконечный треугольник, который обычно выражается в виде скорости. Общее выражение для криволинейного ОСП в случае балки на двух
опорах принимает следующий вид: T. x » =Ah sin-j — +Sin — — — I -.. . ТТ Х+ы Людмила Фирмаль
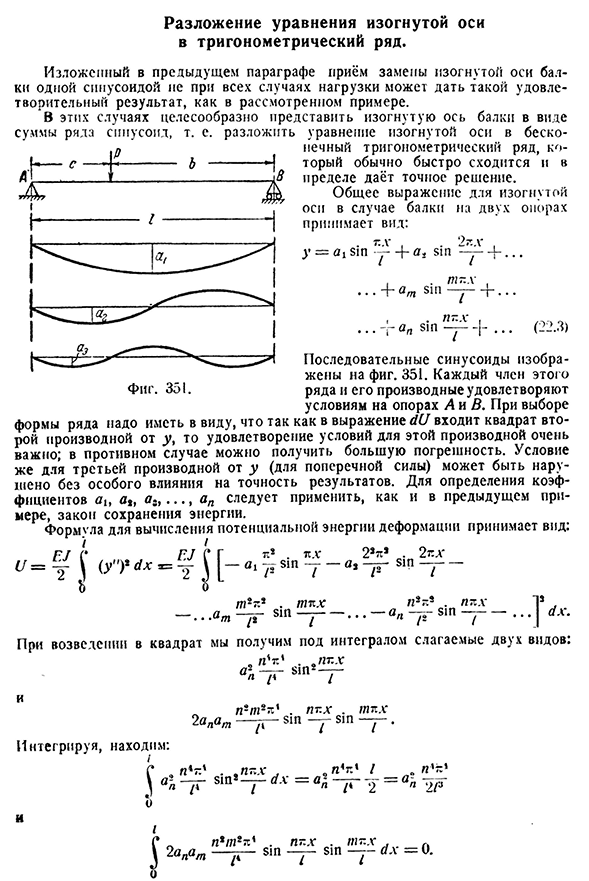
и Н^+.. . … Золото X ,. .. — г » Син.. . Непрерывная синусоидальная волна показана на рисунке. При выборе формы ряда 351 следует отметить, что выполнение условий этой производной очень важно, так как Формула d(J) включает квадрат второй производной y, а условие третьей производной Y (в случае поперечной силы) может быть нарушено без особого влияния на точность результата.
Определить коэффициент alf A2 как t… Кроме того, АП, как и в предыдущем примере, должен применять закон сохранения энергии. Формула для расчета потенциальной энергии деформации принимает вид: I I EJ CI (y»? ООО » ТД » х=е^J является \ ЛГ-^З И Н-Г-а — Си. n2G. х (22.3) т*т * ТТН~г Я п * т*. Золото x I s, s в грехе — — — — — -.. . Дж Д х При возведении в квадрат мы получаем два вида условий
- интеграции: р р р Девять. ЗЗ’РЖ. / Z7ZX al-sin2— • • • И л P2T2l1. полигликомплекса ТТГ^ПА Т грех-см -. Интеграция, мы находим: С 9Р * Т>. Золото X… Я а нят Ы В Н Р2 2/3 б [I/135]разложение криволинейного уравнения в систему 431 Таким образом, мета возможной энергии деформации выражение: Около- Н=ОО Т. Е. У! +2 ′ a2+ • • • +» 4 ′ +. .. ] =»N>°NN-1 потенциальная энергия искажения выражается как функция общих координат АП и представляет собой потенциальную энергию, накопленную отдельно при изгибе пучка для каждой
синусоиды. Переместите Луч в очень близкое положение равновесия рядом с ним и создайте уравнение сохранения энергии. Вы можете просто оставить остальное без изменений и изменить любой из коэффициентов Дэна, чтобы переместить Луч в соседнее положение равновесия. Тогда вместо термина AP sin — выражение (22.3) введет значение (AP+dan) sin-y, и все остальные термины будут содержать это значение. В этом случае изменяется полная энергия деформации, соответствующая только изгибу балки. РХ nusoide АП син-у. Таким образом, увеличение потенциальной
энергии деформации за счет изменения коэффициента ап становится равным… дю е Ж. , ^=- ^- Р<1AP= - ^п^Paap. Это приращение дол Людмила Фирмаль
жно быть численно равно уменьшению потенциальной энергии внешней независимой силы при изменении координат АП. Рассмотрим случай нагружения балки двух опор концентрированным лоем Р, приложенным на расстоянии С от левой опоры(рис. 351). Отклонение этой силы равносильно. — Позже. 2шт, нет.. ППС г С=а изм-п+грех-грех-как. С увеличением этого отклонения путем изменения координат точки доступа к потенциальная энергия груза уменьшается на величину дуп, изменяя прогиб ду=да=Р СК\дуп=р Дэн грех г. Составим уравнение сохранения энергии: dU-dUp, или K’EJ n L nizc а НД а н = р д А Н грех — , Т^ЭЖ (2 ′ 2.4) 11 Луч и потемпо Рассмотрим случай нагружения балки на двух опорах концентрированным си — » под Ра- Откуда (22.5) Получать 7СС. 7SH
7С и Н Т Тогда уравнение отклонения PP G. = — — — — — — Грех — ^СЗ л Н=со PP2V1S•я ННН-З. С. Н-ПК • тс* (22.6)432 приближенное уравнение[гл. XXI Заметим, что соответствующая сила также будет мала, ее работа будет мала во 2-м порядке и не войдет в Формулу накопления энергии, как показано в§ 126. Если сила приложена к середине пролета и вы ищете отклонение в том же сечении, применяя формулу (22.6)、 И Х=2/. (22.7) Этот ряд сходится очень быстро, достаточно сохранить только первый член. П р и М Е Р95. Приведите примерную формулу для криволинейной оси балки, показанной на рисунке. 352 непрерывная нагрузка может быть заменена системой основной концентрации Q de. Прогиб секции dy- от SK NII с абсциссой X
от таких сил в положении, удаленном от начала координат, можно вычислить по формуле (22.6), заменив P на qdc. Затем Чтобы вычислить валовое отклонение y, нам нужно интегрировать этот ряд с C из O -; консолидируя общие члены ряда, мы получаем: Мне 2 года Один. ср2 КТ tr Грех… Грех. х ~ Т К2/П Я Я Целое число§ 136] общие понятия и методы расчета 433 Разница в скобках равна 11=1.. .. . 1Н=2.. .. .2 ″ с-3.. … . 1бк=4.. . Таким образом, y представляется формулой ql * G1PT. х 2. pth1U-0, 5l5E J I P5S in Z+n5S ln-7j’(2 2 ′ 8 ) п=1,3,5,… Р-2,6,10,… Две линии в скобках быстро сходятся. Оставьте только первый член и вычислите среднее и четвертное отклонение пролета: ql_ _ _ qly i^~0,5^E J~153,0£7 Вместо точного значенияQп У1/^я т т т ф я Э J’ ql * G. Это 2. 2К/1 0.769 Qп-о 5k5EJ[с М4/+25С in4/] −0,5 к*Э J ’ КЖ * г•, 2 * 2К * 3ZБЫЛ]_0.645 КЖ*г%^-0 0.5 к * ж[ы IN4Z * 25С IN4Z] » 0,5 г? Е Г
Смотрите также:
| Прогибы балок от действия поперечной силы | Общие понятия и метод расчёта |
| Приближённый приём вычисления прогибов | Способ сравнения деформаций |

